Навигация
Решаем задачу как задачу ЛП
1. Решаем задачу как задачу ЛП.
2. Если мы получим оптимальные целочисленные решения задачи ЛП, то они являются также и оптимальными решениями задачи ЦЛП.
3. Если мы не получим целочисленных решений, то целевая функция Z1 задачи ЛП становится верхней границей оптимального значения Z задачи ЦЛП, потому что значение целевой функции Z при введении в дальнейшем новых ограничений для получения оптимальных целочисленных решений уменьшается.
4. Затем производится ветвление по одному из нецелочисленных оптимальных решений задачи ЛП. Ветвление осуществляется с использованием некоторых правил по следующей схеме: если n![]() x
x![]() n+1, то 1) x
n+1, то 1) x![]() n; 2) x
n; 2) x![]() n+1, где х – нецелочисленное оптимальное решение задачи ЛП, по которому мы осуществляем ветвление, n – ближайшее целое к х не превышающее х.
n+1, где х – нецелочисленное оптимальное решение задачи ЛП, по которому мы осуществляем ветвление, n – ближайшее целое к х не превышающее х.
Правила ветвления:
1) Выбирается переменная, у которой дробная часть наиболее близка к 0,5.
2) Выбирается переменная с наибольшим приоритетом по какому — либо качественному или количественному значению.
3) Переменная выбирается произвольно.
Ограничения введенные при ветвлении добавляются к ограничениям задачи ЛП.
В каждой из вершин находим оптимальные решения полученных путем добавления новых ограничений задач ЛП – 2 и ЛП – 3. Если не у одной из них мы не получили целочисленных оптимальных решений, то мы выбираем ту вершину, в которой получено наибольшее значение целевой функции и производим дальнейшее ветвление. Так продолжается до получения целочисленного оптимального решения одной из задач ЛП.
Вершина называется прозондированной, если:
1) Мы нашли в ней оптимальное целочисленное решение – решение задачи ЦЛП.
2) В данной вершине нет оптимальных решений задачи ЛП.
3) Значение Z в оптимальном решении задачи ЛП не больше текущей нижней границы.
Прочие вершины называются висящими.
Решение задачи методом целочисленного линейного программирования.
Метод ветвей и границ.
Начальные условия берутся из решения задачи ЛП (решение см. выше).
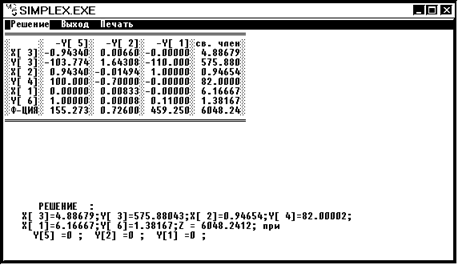
1. Вершина 1 x1 = 6,17 x2 = 0,9 x3 = 4,9 Z1 = 6048,24
Начнем ветвление по x1 = 6,17, тогда получаем дополнительные ограничения а) x1![]() 6 (1 ветвь) б) x2
6 (1 ветвь) б) x2 ![]() 7 (2 ветвь).
7 (2 ветвь).
Решаем сначала ветвь 1. К ограничениям задачи ЛП добавляем ограничение а.
Получаем седьмым ограничением ограничение x1![]() 6;
6;
Решение:
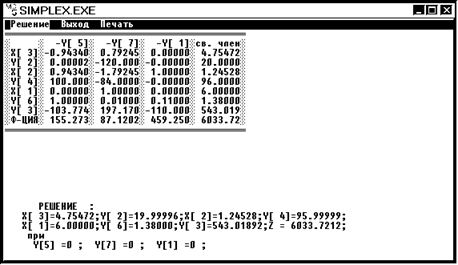
2. Вершина 2 x1 = 6 x2 = 1,2 x3 = 4,8 Z2 = 6033,7212
Мы получили одно целочисленное решение x1 = 6, следовательно дальнейшее ветвление мы будем проводить по x2 или x3.
Решаем ветвь 2. К ограничениям задачи ЛП добавляем ограничение б.
Седьмым ограничением становится ограничение x1![]() 7.
7.
Решение:
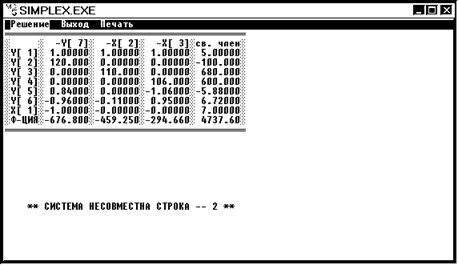
Второй строкой является ограничение задачи ЛП по максимально возможному объему руды с 2 предприятия:
120x1 ![]() 740 или x1
740 или x1![]() 6,16666, что противоречит введенному нами условию 6 (б) x1
6,16666, что противоречит введенному нами условию 6 (б) x1![]() 7. Дальнейшее ветвление из вершины 3 невозможно.
7. Дальнейшее ветвление из вершины 3 невозможно.
Продолжим ветвление из вершины 2. Как было уже сказано выше, мы можем продолжить ветвление по x2 или x3. Продолжим ветвление по x2. x2 = 1,2, следовательно восьмое ограничение для 1 ветви будет x2![]() 1, а для другой x2
1, а для другой x2![]() . Движемся сначала по ветви 1 в вершину 4.
. Движемся сначала по ветви 1 в вершину 4.
Решение:
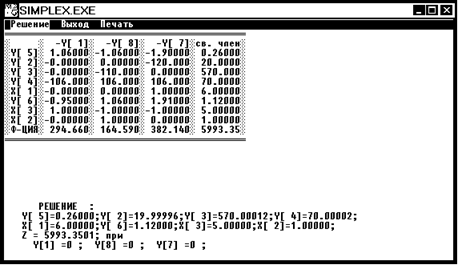
X1 = 6 x2 = 1 x3 = 5 Z4 = 5993,3501
Мы получили, что все три переменных имеют целочисленное значение,
но, чтобы данное решение являлось решением задачи ЦЛП необходимо и достаточно показать, что при ветвлении по ветви 2 в вершине 5 мы получим значение целевой функции Z5 < Z4. Найдем решение в вершине 5.
Решение:
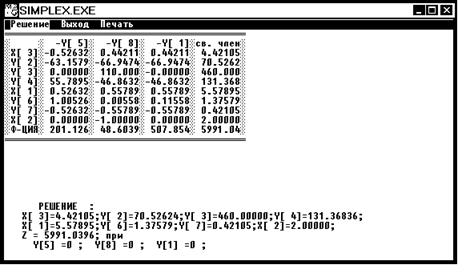
Z5 = 5991,0396, следовательно Z5 < Z4, значит в вершине 4 мы получили решение задачи ЦЛП.
Интерпретация решения с помощью блок – схемы:
 x1=6,1
x1=6,1
Z1=6048 x2=0,9
x3=4,9


x1![]() 6 x1
6 x1![]() 7
7

 x1=6
x1=6
x2=1,2 Система
x3=4,8 несовместна
 |  |
x2![]() 1 x2
1 x2![]() 2
2

 x1=6 x1=5,6
x1=6 x1=5,6
x2=1 x2=2
x3=5 x3=4
Z=5993 Z=5991
| Вершина | Ограничение | № ограничения |
| 2 | x1 | 7 |
| 3 | x1 | 7 |
| 4 | x1 x2 | 7 8 |
| 5 | x1 x2 | 7 8 |

Вывод:
В результате решения я получил, что целочисленное оптимальное решение получается в вершине 4, так как все значения x1=6, x2=1,x3=5 в этой вершине целочисленные и Z5(5991)<Z4(5993), следовательно получено оптимальное решение. Висящая вершина 5 и прозондированные 1,2,3,4.
Плановые задания:
![]() , где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.
, где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.
Для предприятия 1:
![]() тыс. тонн;
тыс. тонн;
Для предприятия 2:
![]() тыс. тонн;
тыс. тонн;
Для предприятия 3:
![]() тыс. тонн.
тыс. тонн.
Нелинейное программирование.
Задача математического программирования называется нелинейной, если нелинейны ограничения или целевая функция.
Задачи нелинейного программирования бывают выпуклого и невыпуклого программирования, с ограничениями и без ограничений, с квадратичными или сепарабельными целевыми функциями. Задачи нелинейного программирования имеют множество экстремальных точек, и сложность решения заключается в выделении глобального оптимума, а не локального как это делается в большинстве классических методов.
Разделяют задачи безусловной и условной оптимизации. Задачами безусловной оптимизации называются задачи оптимизации функции многих переменных без дополнительных ограничений. Существуют следующие методы безусловной оптимизации: покоординатного спуска, градиентные, сопряженных направлений, метод Ньютона. Задачами условной оптимизации называются задачи о оптимизации целевой функции многих переменных f(x1, …, xn) при условии, что эти переменные удовлетворяют следующим ограничениям:
qi(x1, …, xn) = 0, ![]()
или
dj(x1, …, xn) ![]() 0,
0, ![]()
Решение задачи основывается на линейной или квадратичной аппроксимации целевой функции для определения приращений x1, …,xn на каждой итерации.
Существуют также приближенные методы решения нелинейных задач. Это методы основанные на методе кусочно-линейной аппроксимации. Точность нахождения решений зависит от количества интервалов, на которых мы находим решение линейной задачи, максимально приближенной к нелинейной. Такой метод позволяет производить расчеты с помощью симплекс-метода. Обычно в линейных моделях коэффициенты целевой функции постоянны и не зависят от значения переменных. Однако существует ряд задач, где затраты зависят от объема нелинейно. Такие задачи решаются следующим способом: решают задачу ЛП с коэффициентами целевой функции при максимальных значениях переменных. Если в решении мы получили переменные, для которых брались коэффициенты, значит задача решена. В противном случае мы изменяем коэффициенты при целевой функции на коэффициенты при вновь полученных значениях переменных и решаем полученную задачу ЛП. Так мы повторяем до тех пор, пока не будет получено на двух последующих шагах одно и то же решение.
Решение задачи нелинейного программирования.
Метод кусочно – линейной аппроксимации.
В нашей задаче есть такая величина, как коэффициент увеличения затрат при нагрузке, который не использовался нами при решении задачи методами ЛП и ЦЛП. Собственно этот коэффициент и введен для превращения задачи в нелинейную путем нелинейной зависимости между увеличением затрат и загрузкой предприятий.
Составим таблицу:
| № предприятия | Коэффи- Циент затрат % | Количе-ство составов | Коэфф. измене-ния затрат | Затраты на 1т у.е. | Доход | Прибыль На 1т у.е. | Прибыль на 1 состав у.е. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 100 | 6,17 | 1 | 6 | 11,64 | 5,64 | 676,8 | |
| 70 – 100 | 4.31–6,16 | 1,4 | 8,4 | 3,24 | 388,8 | ||
| 50 – 70 | 3,08–4,31 | 1,6 | 9,6 | 2,04 | 244,8 | ||
| 30 – 50 | 1,85–3,08 | 1,7 | 10,2 | 1,44 | 172,8 | ||
| до 30 | до 1,85 | 1,8 | 10,8 | 0,84 | 100,8 | ||
| 100 | 6,18 | 1 | 7 | 11,175 | 4,175 | 459,25 | |
| 70 – 100 | 4,33-6,18 | 1,2 | 8,4 | 2,775 | 305,25 | ||
| 50 – 70 | 3,09-4,33 | 1,4 | 9,8 | 1,375 | 151,25 | ||
| 30 – 50 | 1,85-3,09 | 1,5 | 10,5 | 0,675 | 74,25 | ||
| до 30 | до 1,85 | 1,7 | 11,9 | - 0,725 | - 79,75 | ||
| 100 | 5,66 | 1 | 8 | 10,78 | 2,78 | 294,66 | |
| 70 – 100 | 3,96-5,66 | 1,3 | 10,4 | 0,38 | 40,28 | ||
| 50 – 70 | 2,83-3,96 | 1,6 | 12,8 | - 2,02 | - 214,12 | ||
| 30 – 50 | 1,7 – 2,83 | 1,7 | 13,6 | - 2,82 | - 298,92 | ||
| до 30 | до 1,7 | 1,9 | 15,2 | - 4,42 | - 458,52 |
Где доход (Д) рассчитывается по формуле:
![]() , где
, где
Ц – цена готовой продукции, Е – извлечение, a - содержание полезного компонента.
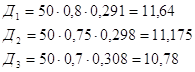
Прибыль (П) рассчитывается по формуле:
П = Д – З , где Д – доход, З – затраты.
Затраты (З) рассчитываются по формуле:
![]() , где С – затраты на добычу, транспортировку и переработку,
, где С – затраты на добычу, транспортировку и переработку, ![]() - коэффициент изменения затрат.
- коэффициент изменения затрат.
1. Пусть x1, x2, x3 принимают свои максимальные значения, тогда
Z1 = 676,8x1 + 459,25x2 + 294,66x3![]() MAX
MAX
Ограничения:
x1 + x2 + x3 =12 – по количеству составов;
x1![]() 6,17 - максимальный объем добычи руды с предприятия 1;
6,17 - максимальный объем добычи руды с предприятия 1;
x2![]() 6,18 - максимальный объем добычи руды с предприятия 2;
6,18 - максимальный объем добычи руды с предприятия 2;
x3![]() 5,66 - максимальный объем добычи руды с предприятия 3;
5,66 - максимальный объем добычи руды с предприятия 3;
0,96x1 + 0,11x2 – 0,95x3![]() 0 – по максимально допустимому содержанию полезного компонента в руде;
0 – по максимально допустимому содержанию полезного компонента в руде;
-0,84x1 + 1,06x3![]() 0 – по минимально допустимому содержанию
0 – по минимально допустимому содержанию
полезного компонента в руде.
Решение 1.

x1 = 6,17 x2 = 0,95 x3=4,88 Z1 = 6048,24
2. Так как x1=6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z2 будет равен 676, 8.
Так как x2=0,95; x2 < 1,87, то коэффициент при x2 в целевой функции Z2 будет равнятся -79,75.
Так как x3=4,88; 3,96 < 4,88 <5,66, следовательно x3 попадает в интервал 3,96 – 5,66, следовательно коэффициент при x3 в целевой функции Z2 будет равен 40,28.
Следовательно Z2 = 676,8x1 – 79,75x2 + 40,28x3
Решение 2.
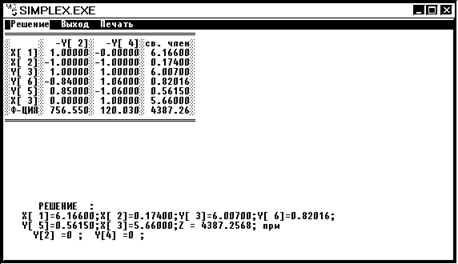
x1 = 6,17 x2 = 0,17 x3 = 5,66 Z2 = 4387,26
3. Так как x1=6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z3 будет равен 676, 8.
Так как x2=0,17; x2 < 1,87, то коэффициент при x2 в целевой функции Z3 будет равнятся -79,75.
Так как x3=5,66 – максимально возможный, то коэффициент при x3 в
целевой функции Z3 будет равен 294,68.
Следовательно Z3 = 676,8x1 – 79,75x2 + 294,68x3
Решение 3.
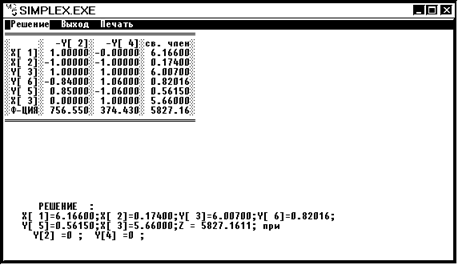
x1 = 6,166 x2 = 0,17 x3 = 5,66 Z3 = 5827,16
Вывод:
Так как на третьем шаге мы получили значения переменных равных значениям переменных на втором шаге, то мы получили искомое решение задачи нелинейного программирования. Третий шаг, за счет того, что значения коэффициента при x3 были увеличены с 40,28 до 294,68, улучшил целевую функцию Z3 на 5827,16 – 4387,26 = 1439,9 у.е.
Плановые задания предприятиям.
![]() , где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.
, где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.
Для предприятия 1:
![]() тыс. тонн;
тыс. тонн;
Для предприятия 2:
![]() тыс. тонн;
тыс. тонн;
Для предприятия 3:
![]() тыс. тонн.
тыс. тонн.
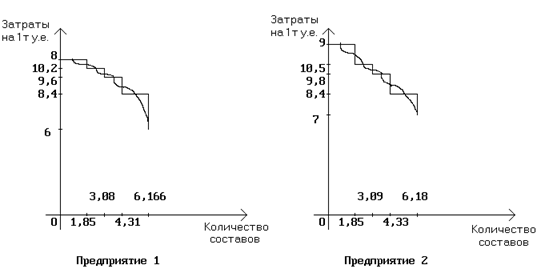
Аппроксимация кривой зависимости затрат от количества составов. Примеры графиков для предприятий 1 и 2.
![]()
Динамическое программирование. (ДП)
Динамическими называются задачи экономики, организации и управления, в которых необходимо распределять ресурсы на каждом этапе какого – либо промежутка (времени). Формулировка задачи ДП:
Имеется некая система S, находящаяся в первоначальном состоянии S. Данная система имеет какие – либо параметры. При переходе системы из одной точки в другую необходимо в каждый момент времени выбирать направление дальнейшего движения из нескольких допустимых направлений при условии, что каждому направлению соответствует своя эффективность (параметры системы изменяются по разному), и необходимо таким образом спланировать маршрут из начальной точки в конечную, чтобы критерий эффективности достигал экстремального значения.
Иными словами из множества допустимых управлений U=(U1, U2, …, Un) необходимо найти оптимальное, при котором система переходит из своего начального состояния в конечное таким образом, что критерий оптимальности W достигает своего максимума.
Динамическое программирование представляет собой метод оптимизации многошаговых процессов по шагам. Локальный оптимум на каждом шаге должен рассчитываться не как оптимальный на данном этапе, а как дающий максимальное значение критерия оптимальности в конце движения. Несоблюдение этого правила приводит к серьезным ошибкам, поэтому при решении задач ДП двигаются обычно из конца пути в начало, рассчитывая затраты при движении в каждом направлении, а затем из начала в конец, находя локальный оптимум из рассчитанных затрат на каждом шаге. Таким образом получаем максимальное значение критерия оптимальности.
В основе расчетов методом динамического программирования лежит принцип Беллмана. Он звучит:
оптимальное управление обладает тем свойством, что какавы бы ни были достигнутые состояния и решения до данного момента, последующее решение должно составлять оптимальное поведение относительно состояния, достигнутого на данный момент.
Решение задачи динамического программирования.
Распределение ресурсов предприятиям.
Данные возьмем из задачи нелинейного программирования: количество составов и прибыль на 1 состав для каждого предприятия:
Предприятие 1.
| Количество составов | Прибыль на 1 состав |
| 6,17 | 676,8 |
| 4,31 – 6,17 | 388,8 |
| 3,08 – 4,31 | 244,8 |
| 1,85 – 3,08 | 172,8 |
| до 1,85 | 100,8 |
Предприятие 2.
| Количество составов | Прибыль на 1 состав |
| 6,18 | 459,25 |
| 4,33 – 6,18 | 305,25 |
| 3,09 – 4,33 | 151,25 |
| 1,85 – 3,09 | 74,25 |
| до 1,85 | -78,75 |
Предприятие 3.
| Количество составов | Прибыль на 1 состав |
| 5,66 | 294,68 |
| 3,96 – 5,66 | 40,28 |
| 2,83 – 3,96 | -214,12 |
| 1,7 – 2,83 | -298,92 |
| до 1,7 | -458,52 |
Количество составов,выделенных всем трем предприятиям (N), равно 14.
Рассчитаем эффективность использования средств предприятиями. Для этого прибыль на один состав умножим на количество составов, при которых достигается эта прибыль на каждом из предприятий.
![]() , где n – количество составов, Pn – прибыль при этом количестве составов.
, где n – количество составов, Pn – прибыль при этом количестве составов.
| Количество составов | Предприятие 1 | Предприятие 2 | Предприятие 3 |
| 1 | 100,8 | -78,15 | -458,52 |
| 2 | 345,6 | 148,5 | -597,94 |
| 3 | 518,4 | 222,75 | -642,36 |
| 4 | 979,2 | 605 | 161,12 |
| 5 | 1944 | 1526,25 | 201,40 |
| 6 | 2332,8 | 1831,5 | 1768,08 |
Рассчитаем ![]() - максимально возможное количество составов для предприятий 1 и 2.
- максимально возможное количество составов для предприятий 1 и 2. ![]() составов. Теперь рассчитаем минимально возможное количество составов для предприятий 1 и 2, исходя из того, что максимально возможное количество составов для предприятия 3 равно
составов. Теперь рассчитаем минимально возможное количество составов для предприятий 1 и 2, исходя из того, что максимально возможное количество составов для предприятия 3 равно ![]() = 6 составов, тогда
= 6 составов, тогда ![]() составов. Составим таблицу выделения средств двум предприятиям (1 и 2). Здесь x - общее количество ресурсов (составов) для двух предприятий; x = x1 + x2; 0
составов. Составим таблицу выделения средств двум предприятиям (1 и 2). Здесь x - общее количество ресурсов (составов) для двух предприятий; x = x1 + x2; 0![]() x1
x1![]() 6 – допустимое количество составов для предприятия 1; 0
6 – допустимое количество составов для предприятия 1; 0 ![]() x2
x2![]() 6 – допустимое количество составов для предприятия 2. Отсюда видно, что 0
6 – допустимое количество составов для предприятия 2. Отсюда видно, что 0 ![]() x
x![]()
![]() , однако количество составов для предприятия 3 не может превышать 6, следовательно x
, однако количество составов для предприятия 3 не может превышать 6, следовательно x![]()
![]() , следовательно
, следовательно ![]()
![]() x
x![]()
![]() ; 8
; 8![]() x
x![]() 12. q1, q2 – эффективность использования средств предприятиями 1 и 2 соответственно взятая из предыдущей таблицы. W2 = q1 + q2 – суммарная эффективность обоих предприятий.
12. q1, q2 – эффективность использования средств предприятиями 1 и 2 соответственно взятая из предыдущей таблицы. W2 = q1 + q2 – суммарная эффективность обоих предприятий.![]() Наибольшую суммарную эффективность для каждого значения x будем подчеркивать.
Наибольшую суммарную эффективность для каждого значения x будем подчеркивать.
| x | x1 | X2 | Эффективность | ||
| q1 | q2 | W2 | |||
| 8 | 2 | 6 | 345,6 | 1831,5 | 2177,1 |
| 3 | 5 | 518,4 | 1526,25 | 2044,65 | |
| 4 | 4 | 979,2 | 605 | 1584,2 | |
| 5 | 3 | 1944 | 222,75 | 2166,75 | |
| 6 | 2 | 2332,8 | 148,5 | 2481,3 | |
| 9 | 3 | 6 | 518,4 | 1831,5 | 2349,9 |
| 4 | 5 | 979,2 | 1526,25 | 2505,45 | |
| 5 | 4 | 1944 | 605 | 2549 | |
| 6 | 3 | 2332,8 | 222,75 | 2555,55 | |
| 10 | 4 | 6 | 979,2 | 1831,5 | 2810,7 |
| 5 | 5 | 1944 | 1526,25 | 3470,25 | |
| 6 | 4 | 2332,8 | 605 | 2937,8 | |
| 11 | 5 | 6 | 1944 | 1831,5 | 3775,5 |
| 6 | 5 | 2332,8 | 1526,25 | 3859,05 | |
| 12 | 6 | 6 | 2332,8 | 1831,5 | 4164,3 |
Теперь составим таблицу выделения средств всем трем предприятиям. Так как N – общее количество составов равно 14, а максимально возможное количество составов для предприятий 1 и 2 ![]() =12, то всем трем предприятиям может быть выделено 13 или 14 составов. W3 – суммарная эффективность всех трех предприятий.
=12, то всем трем предприятиям может быть выделено 13 или 14 составов. W3 – суммарная эффективность всех трех предприятий.
| Количество Составов | x3 | x | Эффективность использования ресурсов | ||
| q3 | W2 | W3 | |||
| 13 | 1 | 12 | -458,52 | 4164,3 | 3705,78 |
| 2 | 11 | -597,94 | 3859,05 | 3261,11 | |
| 3 | 10 | -642,36 | 3470,25 | 2827,89 | |
| 4 | 9 | 161,12 | 2555,55 | 2716,67 | |
| 5 | 8 | 201,4 | 2481,3 | 2682,7 | |
| 14 | 2 | 12 | -597,94 | 4161,3 | 3563,36 |
| 3 | 11 | -642,36 | 3859,05 | 3216,69 | |
| 4 | 10 | 161,12 | 3470,25 | 3631,12 | |
| 5 | 9 | 201,4 | 2555,55 | 2756,95 | |
| 6 | 8 | 1768,08 | 2481,3 | 4249,38 | |
W3 максимальное равно 4249,38, следовательно Z = 4249,38.
x3 = 6; x2 = 2; x3 = 6.
Вывод:
В результате решения задачи динамического программирования я получил, что максимальное значение целевой функции Z = ![]() = 4249,38 получается при количестве составов, выделенных 3 предприятиям N = 14, и количестве составов выделенных предприятию 3 x3 = 6. При этом количество составов для предприятий 1 и 2 равно 8. Максимальная эффективности использования 8 составов предприятиями 1 и 2 достигается при выделении предприятию 1 - 6 составов, а предприятию 2 – 2 состава, и она равна 2481,3. Следовательно x1 = 6, x2 = 2, x3 = 6, Z = 4249,38.
= 4249,38 получается при количестве составов, выделенных 3 предприятиям N = 14, и количестве составов выделенных предприятию 3 x3 = 6. При этом количество составов для предприятий 1 и 2 равно 8. Максимальная эффективности использования 8 составов предприятиями 1 и 2 достигается при выделении предприятию 1 - 6 составов, а предприятию 2 – 2 состава, и она равна 2481,3. Следовательно x1 = 6, x2 = 2, x3 = 6, Z = 4249,38.
Плановые задания предприятиям:
![]() , где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.
, где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.
Для предприятия 1:
![]() тыс. тонн;
тыс. тонн;
![]() тыс. тонн;
тыс. тонн;
![]() тыс. тонн.
тыс. тонн.
Графическая интерпретация решений.
Похожие работы
... , 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные. Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций. Линейное программирование Несмотря на требование линейности целевой функции и ограничений, в рамки линейного ...
... -бухгалтер должен: а) потребовать недостающие материалы у проверяемой организации; б) составить сообщение о невозможности дачи заключения; в) заявить письменное ходатайство о предоставлении ему дополнительных документов. 1. Исследование операций по заработной плате Задачей судебно-бухгалтерской экспертизы при исследовании операций по труду и заработной плате является активизация ...
... и направление ветра, плотность воздуха и др. 4. Эквифинальность. Рано или поздно, самолет вынужден будет приземлится или разобьется. Т.о. скорости, ускорения, моменты и силы будут равны нулю. Исследование операций Задача 1 Авиакомпания «Небесный грузовик», обслуживающая периферийные районы страны, располагает А1 самолетами типа 1, А2 самолетами типа 2, А3 самолетами типа 3, которые она ...
... Лагранжа: L(x,u)=F(x)+u1g1(x)+u2g2(x)=-2x12-x22-4x1x2+6x1+1,5x2+u1 (2,5x1-x2–7)+ u2 (3x1+2,5x2-13). Получим уравнения седловой точки, применяя теорему Куна-Таккера: i=1;2 Объединим неравенства в систему А, а равенства в систему В: Система А: Система В: Перепишем систему А: 6-4x1-4x2+2,5u1+3u2 <0 1,5-4x1-2x2-u1+2,5u2 <0 2,5x1-x2–7³0 3x1+2,5x2–13³0 4)Введем новые ...
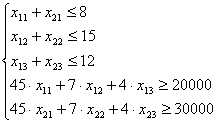
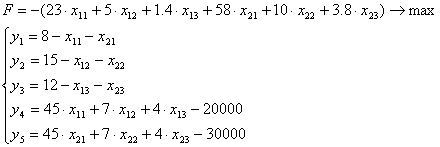
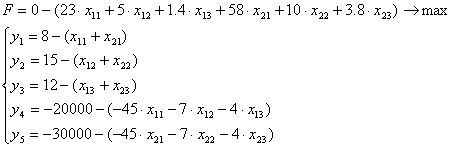
0 комментариев