Навигация
Отечественные методы решения
2.4.2 Отечественные методы решения
Подход, в значительной мере аналогичный работам [45-51] был предложен в работе [41]. Из-за небольшого объема в ней уделено недостсточное внимание вопросам практической реализации, объяснены не все обозначения и не приведены результаты численного моделирования. В целом это значительно снижает практическую ценность статьи. Приведем основные положения этой работы.
Прямая задача
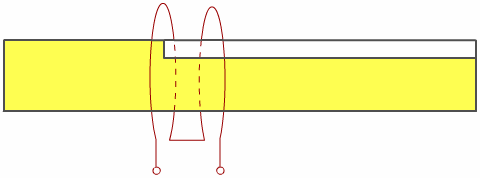
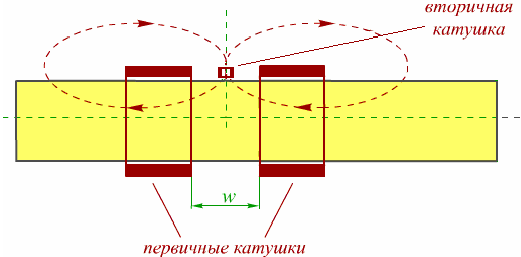
Пусть круговой виток радиусом а с током I находится в точке P=Ps(r,j,z), jО(-p,p) вблизи немагнитного ОК, занимающего область V. Пусть ОК обладает электрической проводимостью s=s0Чs(Р) являющейся произвольной функцией координат. Требуется по N измерениям величины э.д.с. определить s как функцию координат точек PОV. Причем i-ое измерение э.д.с. будем проводить на i-ом измерительном круговом витке с координатами Pi=Pi(r,j,z) i=1,N при неизменных частоте и расположении возбуждающего витка.
В общем случае напряженность электрического поля Е определяется через векторный магнитный потенциал А, причем А = А0 + Авн, где А0 - возбуждающий, а Авн - вносимый потенциалы.
| | (2.4.14) |
Вводя функцию Грина G(p,p0) получим
| | (2.4.15) |
При этом вносимая напряженность электрического поля
| Eвн = -jЧwЧAвн | (2.4.16) |
Вносимая э.д.с., наводимая в i-ом витке
| | (2.4.17) |
где функция Грина G(P,P0) имеет вид
| | (2.4.18) |
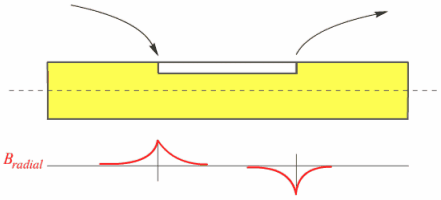
В дальнейшем рассмотрим случай, при котором V-полупространство (r>0,\j\0
(6.2)
Непрерывную функцию y(х) называют штрафом, если y(х)=0 для хО Х и y(х)>0 в противном случае. Функция y(х) должна быть выбрана таким образом, чтобы решение задачи (6.2) сходилось при b®0 к решению исходной задачи (6.1) или, по крайней мере, стремилось к нему.
Приведем часто используемые выражения для штрафа :
| | (6.3) |
| | (6.4) |
| | (6.5) |
Наибольшее применение находит штраф (6.3). Выражение (6.5) гарантирует конечность метода при любом k>0.
При численной реализации метода штрафных функций возникают проблемы выбора начального значения параметра b и способа его изменения. Сложность состоит в том, что выбор достаточно малого b увеличивает вероятность сходимости решения (6.2) к решению (6.1), а скорость сходимости градиентных методов вычисления точек минимума (6.2), как правило, падает с убыванием величины b .
6.2 Релаксационные методы
Релаксационным методом называют процесс построения последовательности точек {хk: хk О X , j( хk+1 ) Ј j( хk ) ; k=0,1... }. Основными представителями этого класса являются методы спуска, алгоритм которых состоит из следующих шагов :
Выбор начального приближения х0
Выбор в точке хk направления спуска -sk
Нахождение очередного приближения хk+1 = хk - akЧsk , где длина шага ak>0
Различия методов состоят в выборе либо направления спуска, либо способа движения вдоль выбранного направления. В последнем случае обычно используют одномерную минимизацию функции хk+1(a) = хk - aЧsk (при этом точность вычисления точки минимума функции хk+1(a) следует согласовывать с точностью вычисления значений функции j(х)) или способ удвоения a(величина шага удваивается пока выполняется условие j(хk+1) Ј j(хk) ).
6.2.1 Метод условного градиента
Идея метода заключается в линеаризации нелинейной функции j(х). В этом методе выбор направления спуска осуществляется следующим образом :
Линеаризируя функцию j(х) в точке хК получаем Ф(х)= j( хk ) + ( j( хk )’ , х - хk )
Минимизируя линейную функцию Ф(х) на множестве Х находим хmin
Направление спуска получаем как -sk = хmin - хk
Таким образом итерация метода имеет вид: xk+1=xk+akЧ(sk+1 - xk) , sk+1=arg min(Сf(xk),x).
Основное преимущество метода проявляется в случае задания допустимого множества с помощью линейных ограничений. В этом случае получаем задачу линейного программирования, решаемую стандартными методами(например симплексным).
Похожие работы
... поверхностной трещины, когда однородное (или неоднородное) поле пересекает поверхностную трещину в ферромагнитной пластине (рис.4). Рисунок 4. Поток магнитного рассеяния для двумерного случая в поперечном сечении ферромагнитной пластины Считается, что однородное магнитное поле распространяется слева направо. Вблизи дефекта поток разделяется на две части. Одна часть потока пытается обогнуть ...
... приборов и визуальные наблюдения за процессом позволяют оперативно реагировать на возможные отклонения, во многом обеспечивает качество сварных соединений. При сварке ответственных конструкций используют системы автоматического управления и регулирования параметров режима с помощью датчиков автоматического контроля, встроенных в сварочное оборудование. В некоторых случаях ведут непрерывную запись ...
... в процесс, были одобрены, спланированы, получили материально-техническую поддержку и управлять в целях заинтересованных сторон. Глава 3. Перспектива автоматизации системы неразрушающего контроля изделий на предприятиях машиностроительного профиля 3.1 Комплексная технология АУЗК В связи с высоким техническим уровнем современного производства методом и средством НК предъявляют высокие ...
... , повысить вероятность выявления дефектов и, с другой стороны, снизить различные технико-экономические затраты на проведение контроля. 2. Проектирование системы контроля знаний 2.1 Общая структура системы По своей логической структуре система состоит из трёх частей: - подсистемы конфигурирования теста; - подсистемы тестирования; - подсистема сервиса. ...
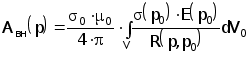
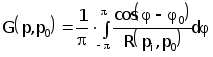
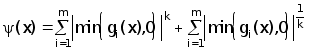




0 комментариев