Навигация
4. Составление нового базиса
4.1 Выбор элемента для введения в базис.
В базис вводится любой столбец, для которого Dk j( dk )
ak =
ak-1
ck-1
bk =
dk-1
bk-1
dk =
ck-1
ck =
dk-1
hk+2 =
hk-hk-1
hk-hk-1
dk =
bk-hk+2
ck =
ak+hk+2
Если ( hk Ј e ) то xmin=min{ j(ck) , j(dk) } иначе k++ и переход к шагу II
Следует отметить, что на каждом шаге кроме первого, производится только одно вычисление значения функции j(x).
Легко показать, что для получения оптимальной последовательности отрезков, стягивающихся к точке минимума, необходимо положить lk = Fk-1/Fk , где F - число Фибоначчи.
8.2 Метод Фибоначчи
Решая вопрос, при каких значениях параметра l за конечное число итераций N мы получим отрезок минимальной длины, получим l = lN = FN-1/FN. Иначе говоря, для поиска минимума первоначально необходимо найти число Фибоначчи N такое, что FN+10000XXXX}
fHypTg:=(( apDT AND apHypTg ) = apHypTg);
if fHypTg then
begin
si0[ 1 ]:=si[ 1 ]; {si1 - conductivity about bottom of slab}
si0[ 2 ]:=par0[ 2 ]; {si2 - conductivity about top of slab}
si0[ 3 ]:=par0[ 3 ]; {Beta - ratio of approx.}
si0[ 4 ]:=par0[ 4 ]; {Gamma- ratio of approx.}
mCur:=4;
end
else
if(( apDT AND apExp ) = 0 ) then {It's not an EXP approx.}
begin
for i:=1 to nPoints do si0[ i ] :=si [ i ]; {SI data from file}
mCur:=nPoints;
end
else
begin
si0[ 1 ]:=si[ 1 ]; {siI - conductivity about bottom of slab}
si0[ 2 ]:=si[ nPoints ]; {siE - conductivity about top of slab}
si0[ 3 ]:=par0[ 1 ]; {Alfa- ratio of approx.}
mCur:=3;
end;
setApproximationType( apDT ); {approx. type for direct problem}
setApproximationData( si0, mCur ); {approx. data for direct problem}
nApprox := ( nApprox AND $0F ); {XXXXYYYY->0000YYYY}
fHypTg := (( nApprox AND apHypTg ) = apHypTg );
fMulti := (( nApprox AND apExp ) = 0 ) AND NOT fHypTg; {It's not an EXP approx.}
if fMulti then
begin
for i:=1 to nPoints do
begin
Gr[ 1,i ]:=SiMax[ i ];
Gr[ 2,i ]:=SiMin[ i ];
Rg[ i ]:=( Gr[ 1,i ] + Gr[ 2,i ] )/2; {zero estimate of SI}
Rgs[ i ]:=1E33; {biggest integer}
end;
mLast:=nPoints; {loop for every node of approx.}
mCur :=1; {to begin from the only node of approx}
end
else
if fHypTg then
begin
Gr[ 1,1 ]:= siMax[ 1 ]; Gr[ 2,1 ]:= siMin[ 1 ]; Rgs[ 1 ]:=1E33;
Gr[ 1,2 ]:=parMax[ 2 ]; Gr[ 2,2 ]:=parMin[ 2 ]; Rgs[ 2 ]:=1E33;
Gr[ 1,3 ]:=parMax[ 3 ]; Gr[ 2,3 ]:=parMin[ 3 ]; Rgs[ 3 ]:=1E33;
Gr[ 1,4 ]:=parMax[ 4 ]; Gr[ 2,4 ]:=parMin[ 4 ]; Rgs[ 4 ]:=1E33;
for i:=1 to 4 do Rg[ i ]:=( Gr[ 1,i ] + Gr[ 2,i ] )/2;
mLast:=1;
mCur:=4;
end
else
begin
Gr[ 1,1 ]:= siMax[1]; Gr[2,1]:= siMin[1]; Rgs[ 1 ]:=1E33;
Gr[ 1,2 ]:= siMax[nPoints]; Gr[2,2]:= siMin[nPoints]; Rgs[ 2 ]:=1E33;
Gr[ 1,3 ]:= parMax[1]; Gr[2,3]:= parMin[1]; Rgs[ 3 ]:=1E33;
for i:=1 to 3 do Rg[ i ]:=( Gr[ 1,i ] + Gr[ 2,i ] )/2;
mLast:=1;
mCur :=3;
end;
initConst( nLayers, parMaxH, parMaxX , parEps, parEqlB );{set probe params}
end;
procedure directTask; {emulate voltage measurements [with error]}
begin
for i:=1 to nFreqs do
begin
getVoltage( freqs[i], Umr[ i ], Umi[ i ] ); {"measured" Uvn*}
if ( epsU > 0 ) then {add measurement error}
begin
randomize; Umr[ i ]:=Umr[ i ]*( 1 + epsU*( random-0.5 ) );
randomize; Umi[ i ]:=Umi[ i ]*( 1 + epsU*( random-0.5 ) );
end;
end;
writeln('* Voltage measurements have been emulated');
setApproximationType( nApprox ); {approx. type for inverse problem}
setApproximationData( Rg, mCur ); {approx. data for inverse problem}
end;
procedure reduceSILimits; {evaluate SI for m+1 points of approx. using aG}
var
x0, x1, xL, dx, Gr1, Gr2 : real;
j, k : byte;
begin
{----------------------------- get SI min/max for m+1 points of approximation}
dx:=1/( nPoints-1 );
for i:=1 to m+1 do
begin
k:=1;
x1:=0;
x0:=( i-1 )/m;
for j:=1 to nPoints-1 do
begin
xL:=( j-1 )/( nPoints-1 );
if( ( xL < x0 ) AND ( x0 Gr[1,i] )then Rg[i]:=Gr[1,i];
if ( Rg[i] < Gr[2,i] )then Rg[i]:=Gr[2,i];
if m > 1 then {There're more than 1 point of approx.}
begin
Gr1:= Rg[i]+( Gr[1,i]-Rg[i] )*aG; {reduce upper bound}
Gr2:= Rg[i]-( Rg[i]-Gr[2,i] )*aG; {reduce lower bound}
if ( Gr1 < Gr[1,i] )then Gr[1,i]:=Gr1; {test overflow}
if ( Gr2 > Gr[2,i] )then Gr[2,i]:=Gr2;
end;
end;
setApproximationData( Rg , m+1 );
end;
procedure resultMessage; {to announce new results}
begin
if fMulti then
begin
writeln(' current nodal values of conductivity');
write(' si : ');for i:=1 to m do write(Rg[i] :6:3,' ');writeln;
write(' max: ');for i:=1 to m do write(Gr[1,i]:6:3,' ');writeln;
write(' min: ');for i:=1 to m do write(Gr[2,i]:6:3,' ');writeln;
end
else
begin
for i:=1 to nPoints do si[i]:=getSiFunction( ( i-1 )/( nPoints-1 ) );
if fHypTg then
saveHypTgResults
else
saveExpResults;
end;
end;
procedure clockMessage; {user-friendly message}
begin
writeln('***********************************************************');
write( '* approximation points number :',m:3,' * Time '); clock;
writeln('***********************************************************');
end;
procedure done; {final message}
begin
Sound(222); Delay(111); Sound(444); Delay(111); NoSound; {beep}
write('* Task processing time '); clock; saveTime;
writeln('* Status: Inverse problem has been successfully evaluated.');
end;
Begin
about;
loadData;
initParameters;
directTask;
for m:=1 to mLast do
begin
if fMulti then
begin
mCur:=m;
clockMessage;
end;
doMinimization; {main part of work}
setApproximationData( Rg, mCur ); {set new approx. data}
resultMessage;
if(( fMulti )AND( m < nPoints ))then reduceSILimits;
end;
done;
End.
П1.5 Модуль глобальных данных EData
Unit EData;
Interface
Uses DOS;
Const
maxPAR = 40; {nodes of approximation max number}
maxFUN = 20; {excitation frequencies max number}
maxSPC = 4; {support approximation values number}
iterImax = 50; {max number of internal iterations}
Const
apSpline = 1; {approximation type identifiers}
apHypTg = 3;
apExp = 2;
apPWCon = 4;
apPWLin = 8;
Type
Parameters = array[ 1..maxPAR ] of real; {Si,Mu data}
Functionals = array[ 1..maxFUN ] of real; {Voltage data}
SpecialPar = array[ 1..maxSPC ] of real; {Special data}
Var
hThick : real; {thickness of slab}
nPoints : integer; {nodes of approximation number within [ 0,H ]}
nLayers : integer; {number of piecewise constant SI layers within[ 0,H ]}
nFreqs : integer; {number of excitation frequencies}
nStab : integer; {required number of true digits in SI estimation}
epsU : real; {relative error of measurement Uvn*}
nApprox : byte; {approximation type identifier}
incVal : real; {step for numerical differ.}
parMaxH : integer; {max number of integration steps}
parMaxX : real; {upper bound of integration}
parEps : real; {error of integration}
derivType: byte; {1 for right; 2 for central}
Var
freqs : Functionals; {frequencies of excitment Uvn*}
Umr, Umi : Functionals; { Re(Uvn*),Im(Uvn*) for "measured" data}
Uer, Uei : Functionals; { Re(Uvn*),Im(Uvn*) for estimated data}
mu : Parameters; {relative permeability nodal values}
si, si0 : Parameters; {conductivity approximation nodal values}
siMin, siMax : Parameters; {conductivity nodal values restrictions}
par0 : SpecialPar; {alfa,si2,beta,gamma - for exp&HypTg}
parMin,parMax: SpecialPar; {-||- min/max}
zLayer : Parameters; {relative borders of slab layers [0,1]}
Var
aG : real; {scale factor for SImin/max}
Ft : real; {current discrepancy functional value}
fMulti : boolean; {TRUE if it isn't an EXP-approximation}
fHypTg : boolean; {TRUE for Hyperbolic tg approximation}
parEqlB : boolean; {TRUE if b[i]=const}
mCur : integer; {current number of approximation nodes}
inFileName : string; {data file name}
outFileName : string; {results file name}
Var
Rg : Parameters; {current SI estimation}
RgS : Parameters; {previous SI estimation}
Gr : array [ 1..2 ,1..maxPAR ] of real; {SI max/min}
Fh : array [ 1..maxPAR , 1..maxFUN ] of real; {current discrepancies}
Type
TTime=record
H, M, S, S100 : word; {hour,min,sec,sec/100}
end;
Var
clk1, clk2 : TTime; {start&finish time}
procedure loadData; {load all user-defined data from file}
Implementation
procedure loadData;
var
i,eqlB : integer;
FF : text;
begin
assign( FF, outFileName ); {clear output file}
rewrite( FF );
close( FF );
assign( FF, inFileName ); {read input file}
reset( FF );
readln( FF );
readln( FF );
readln( FF, hThick, nPoints, nLayers, nFreqs, nStab, epsU, aG, nApprox );
readln( FF );
for i:=1 to nFreqs do read( FF, freqs[i] );
readln( FF );
readln( FF );
readln( FF );
for i:=1 to nPoints do readln( FF, si[i], siMin[i], siMax[i] );
readln( FF );
readln( FF );
readln( FF , incVal, parMaxH, parMaxX, parEps, derivType, eqlB );
readln( FF );
readln( FF );
for i:=1 to maxSPC do readln( FF, par0[i] , parMin[i] , parMax[i] );
readln( FF );
if ( eqlB=0 )then
begin
for i:=1 to nLayers+1 do read( FF, zLayer[i] );
parEqlB:=false;
end
else parEqlB:=true;
close( FF );
for i:=1 to maxPAR do mu[i]:=1;
end;
Var
str : string;
Begin
if( ParamCount = 1 )then str:=ParamStr(1)
else
begin
write('Enter I/O file name, please: ');
readln( str );
end;
inFileName :=str+'.txt';
outFileName:=str+'.lst';
End.
П1.6 Модуль работы с файлами EFile
Unit EFile;
Interface
Uses
DOS, EData;
function isStable( ns : integer; var RG1,RG2 ) : boolean;
function saveResults( ns,iter : integer ) : boolean;
procedure saveExpResults;
procedure saveHypTgResults;
procedure clock;
procedure saveTime;
Implementation
Var
FF : text;
i : byte;
function decimalDegree( n:integer ) : real;{10^n}
var
s:real; i:byte;
begin
s:=1;
for i:=1 to n do s:=s*10;
decimalDegree:=s;
end;
function isStable( ns:integer ; var RG1,RG2 ) : boolean;
var
m : real;
R1 : Parameters absolute RG1;
R2 : Parameters absolute RG2;
begin
isStable:=TRUE;
m:=decimalDegree( ns-1 );
for i:=1 to mCur do
begin
if NOT(( ABS( R2[i]-R1[i] )*m ) dx ) do
begin
i:=i + 1;
dx:=dx + dh;
end;
siPWConst:=appSigma[ i ];
end;
end;
function siPWLinear( x:real ) : real;{Piecewise linear approximation}
var
dx, dh : real;
i : byte;
begin
if( appCount = 1 )then siPWLinear := appSigma[ 1 ]
else
begin
dh:=1/( appCount-1 );
dx:=0;
i:=1;
repeat
i:=i + 1;
dx:=dx + dh;
until( x B[k] then k1:=k;
for k:=1 to mp1 do A[k1,k]:=-A[k1,k];
A[k1,mCur+1+k1]:=0;
B[k1]:=-B[k1];
for i:=1 to n2 do
if ik1 then
begin
B[i]:=B[i]+B[k1];
for k:=1 to mm1 do A[i,k]:=A[i,k]+A[k1,k];
end;
for i:=mp2 to m21 do
begin
Sx[i]:=B[i-mp1];
Nb[i-mp1]:=i;
end;
for i:=1 to mp1 do Sx[i]:=0;
Sx[1]:=B[k1];
Sx[mp1+k1]:=0;
Nb[k1]:=1;
103:
for i:=2 to m21 do N0[i]:=0;
104:
for i:=m21 downto 2 do
if N0[i]=0 then n11:=i;
for k:=2 to m21 do
if ((A[k1,n11]B[i]/A[i,n11] then
begin
Sx[n11]:=B[i]/A[i,n11]; ip:=i;
end;
end;
end
else
if iq=0 then
begin
N0[n11]:=n11;
goto 104;
end;
end;
Sx[Nb[ip]]:=0;
Nb[ip]:=n11;
B[ip]:=B[ip]/A[ip,n11];
apn:=A[ip,n11];
for k:=2 to m21 do A[ip,k]:=A[ip,k]/apn;
for i:=1 to m1 do
if iip then
begin
ain:=A[i,n11];
B[i]:=-B[ip]*ain+B[i];
for j:=1 to m21 do A[i,j]:=-ain*A[ip,j]+A[i,j];
end;
for i:=1 to m1 do Sx[Nb[i]]:=B[i];
goto 103;
105:
for k:=1 to mCur do Sx[k+1]:=Sx[k+1]+Gr[2,k];
a1:=0;
a2:=1.;
dh:=a2-a1;
r:=0.618033;
tl:=a1+r*r*dh;
tp:=a1+r*dh;
j:=1;
108:
if j=1 then tt:=tl else tt:=tp;
106:
for i:=1 to mCur do Rg[i]:=Zt[i]+tt*(Sx[i+1]-Zt[i]);
getFunctional( 0 );
cv:=abs(Fh[1,1]);
if nFreqs>1 then
for k:=2 to nFreqs do
begin
cv1:=abs(Fh[1,k]);
if cv
Похожие работы
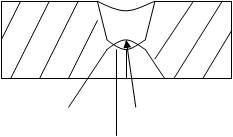
... поверхностной трещины, когда однородное (или неоднородное) поле пересекает поверхностную трещину в ферромагнитной пластине (рис.4). Рисунок 4. Поток магнитного рассеяния для двумерного случая в поперечном сечении ферромагнитной пластины Считается, что однородное магнитное поле распространяется слева направо. Вблизи дефекта поток разделяется на две части. Одна часть потока пытается обогнуть ...
... приборов и визуальные наблюдения за процессом позволяют оперативно реагировать на возможные отклонения, во многом обеспечивает качество сварных соединений. При сварке ответственных конструкций используют системы автоматического управления и регулирования параметров режима с помощью датчиков автоматического контроля, встроенных в сварочное оборудование. В некоторых случаях ведут непрерывную запись ...
... в процесс, были одобрены, спланированы, получили материально-техническую поддержку и управлять в целях заинтересованных сторон. Глава 3. Перспектива автоматизации системы неразрушающего контроля изделий на предприятиях машиностроительного профиля 3.1 Комплексная технология АУЗК В связи с высоким техническим уровнем современного производства методом и средством НК предъявляют высокие ...
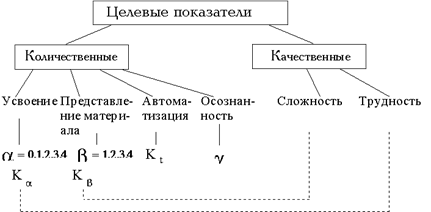
... , повысить вероятность выявления дефектов и, с другой стороны, снизить различные технико-экономические затраты на проведение контроля. 2. Проектирование системы контроля знаний 2.1 Общая структура системы По своей логической структуре система состоит из трёх частей: - подсистемы конфигурирования теста; - подсистемы тестирования; - подсистема сервиса. ...




0 комментариев