Атом водорода. Частица в центрально симметричном поле

10. Атом водорода. Частица в центрально симметричном поле

Пусть , т.е. поле обладает центральной симметрией, тогда . Гамильтониан в координатном представлении имеет вид . Пишем уравнение на собственные векторы:

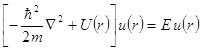
В полярных координатах оператор Лапласа имеет вид

,

где  содержит слагаемые с производными по переменным  и .

Можно показать, что оператор квадрата импульса и гамильтониан коммутируют: 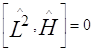. Физически это означает, что L² сохраняется. И  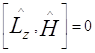тоже, значит операторы  имеют общие собственные векторы.

Положительно заряжённое ядро создаёт поле  или в более общем виде . Вектор , где , , , будет решением уравнения на собственные векторы гамильтониана, при чём

Вектору  в координатном представлении отвечает функция .

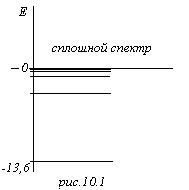
Стационарное состояние электрона в атоме водорода задаётся тремя числами n, l, m, эти числа определяют энергию E_n, момент и проекцию импульса соответствующие этому состоянию, при чём . Это вследствие того, что .

Бор постулировал, что существуют орбиты, на которых электроны не излучают и ещё

1) , где n – номер орбиты,

2) .

Из этих постулатов следует, что

и .

При Z = 1 (водород) и n = 1 .

11. Система тождественных частиц

Пусть система состоит из N частиц, а её состояние задаётся вектором  тогда соответственно

(вероятность обнаружить  частицу в элементе объёма ) = .

,

,

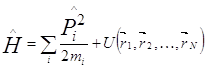где .

В квантовой механике частицы одного сорта тождественны, принципиально неразличимы (рис. 11.1). Пусть у нас имеется две частицы, тогда

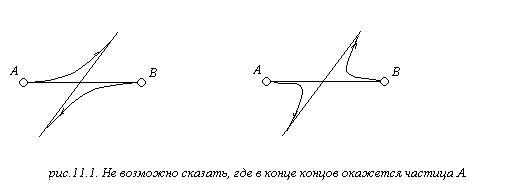
Как это может быть? Так как модуль вектора  постоянен, то вектор может только вращаться вокруг начала координат: . Из условия нормировки следует: , это выполняется только в двух случаях:  и . Так как , возможны две ситуации:

1. , волновая функция симметрична относительно перестановки пары тождественных частиц, такие частицы называются бозоны;

2. , это фермионы.

Принцип Паули гласит, что два фермиона не могут находиться в одном и том же состоянии.

§7. Квантовая статистика

Ели мы при абсолютном нуле температуры будем кидать бозоны в одну энергетическую яму, а фермионы в другую, то картины будут различными: фермионы будут занимать различные энергетические уровни, а бозоны – первый.1)

Если теперь мы будем бозоны трясти, то они как-то распределятся по энергиям, фермионы тоже. Я приведу только результат.