Навигация
Распределение Ферми (для фермионов)
1. Распределение Ферми (для фермионов)
Среднее число частиц при температуре T в определённом состоянии даётся формулой
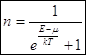
где ![]() – уровень Ферми или химический потенциал. Электроны в металле представляют идеальный фермионный газ.
– уровень Ферми или химический потенциал. Электроны в металле представляют идеальный фермионный газ.
2. Распределение Бозе (для бозонов)
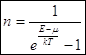
14
Итак, среднее число частиц в состоянии ![]() при температуре T равно:
при температуре T равно:
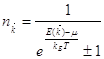 ,
,
где ![]() соответствует фермионам,
соответствует фермионам, ![]() – базонам.
– базонам.
3. Число состояний частицы в определённом интервале энергий. Распределение по энергиям
Число частиц с энергиями в интервале ![]() пропорционально
пропорционально ![]() :
: ![]() . Наша задача найти функцию распределения по энергиям
. Наша задача найти функцию распределения по энергиям ![]() .
.
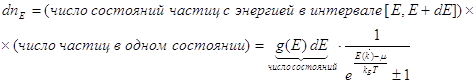
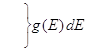
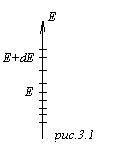 Если мы найдём функцию g(E), тогда автоматически мы найдём и f(E),
Если мы найдём функцию g(E), тогда автоматически мы найдём и f(E), ![]() – число состояний, приходящихся на интервал энергий
– число состояний, приходящихся на интервал энергий ![]() . Это можно условно так изобразить: на шкале энергий отдельные значения энергии (энергия меняется дискретно), число палочек в интервале энергий
. Это можно условно так изобразить: на шкале энергий отдельные значения энергии (энергия меняется дискретно), число палочек в интервале энергий ![]() это как раз будет число состояний
это как раз будет число состояний ![]() . Проблема теперь упирается в нахождение этой функции g(E).
. Проблема теперь упирается в нахождение этой функции g(E).
Мы рассматривали частицу в ящике, и там были найдены возможные состояния, напомню, что любая тройка целых чисел ![]() задаёт состояние с волновой функцией
задаёт состояние с волновой функцией ![]() . Перебирая все тройки чисел, мы получим все возможные состояния. А теперь у нас задача такая: задать интервал энергии и перебрать все возможные состояния, энергия которых попадёт в этот интервал. Задача на первый взгляд страшно трудная, на самом деле решаемая и довольно элементарно. Можно было бы отталкиваться от решения для ящика, но применяется другой трюк более
. Перебирая все тройки чисел, мы получим все возможные состояния. А теперь у нас задача такая: задать интервал энергии и перебрать все возможные состояния, энергия которых попадёт в этот интервал. Задача на первый взгляд страшно трудная, на самом деле решаемая и довольно элементарно. Можно было бы отталкиваться от решения для ящика, но применяется другой трюк более ![]() удобный.
удобный.
Будем считать, что волновая функция частицы не такая, как там было найдено для частицы в ящике, а волновая функция имеет вид ![]() с граничными условиями:1)
с граничными условиями:1)
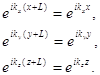
Это означает, что
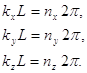
Ну, и
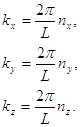
![]() - целые числа
- целые числа
Если б мы рассматривали свободную частицу в пространстве, любой вектор ![]() был бы допустим, когда мы рассматриваем частицу в ящике, то не любые векторы
был бы допустим, когда мы рассматриваем частицу в ящике, то не любые векторы ![]() задают состояния, а каждая компонента вектора
задают состояния, а каждая компонента вектора ![]() должна быть кратной величине
должна быть кратной величине ![]() .
.
![]()
![]()
![]()
![]()
![]()
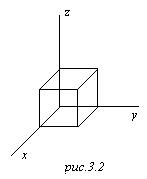
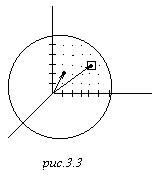 Векторы
Векторы ![]() могут быть такими, как на рис.3.3, они дискретны, проекции вектора
могут быть такими, как на рис.3.3, они дискретны, проекции вектора ![]() должны быть кратны числу
должны быть кратны числу ![]() . Мы имеем дискретный набор точек и теперь мы их можем считать. Мы видим, что на одно состояние в этом пространстве волновых чисел или k-пространстве приходится ячейка с объёмом
. Мы имеем дискретный набор точек и теперь мы их можем считать. Мы видим, что на одно состояние в этом пространстве волновых чисел или k-пространстве приходится ячейка с объёмом ![]() .
.
А теперь мы можем ответить на вопрос о том, сколько состояний приходится на заданный интервал энергии. Для частицы с массой m ![]() . В k-пространстве энергии E отвечает сфера радиуса
. В k-пространстве энергии E отвечает сфера радиуса ![]() , и тогда все точки k-пространства, которые находятся внутри этой сферы, отвечают состояниям, энергия которых меньше E. Тогда число состояний с энергией в интервале [0, E] это будет объём сферы, делённый на объём, приходящийся на одно состояние.
, и тогда все точки k-пространства, которые находятся внутри этой сферы, отвечают состояниям, энергия которых меньше E. Тогда число состояний с энергией в интервале [0, E] это будет объём сферы, делённый на объём, приходящийся на одно состояние.
Число состояний NE с энергиями в интервале [0, E], будет равняться
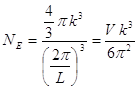 , где V = L3
, где V = L3
А тогда число состояний в интервале ![]() мы получим просто дифференцированием:
мы получим просто дифференцированием:
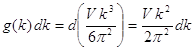
Тогда число частиц, для которых ![]() , равно
, равно
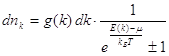
Это не то, что нас интересует. Это не распределение по энергиям – это распределение по волновым числам. А теперь мы вернёмся к распределению по энергиям.
Фермионы с массой m.
![]() , нам теперь надо просто перейти от k к E.
, нам теперь надо просто перейти от k к E.
![]()
![]() .
.
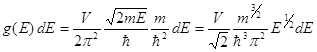
На самом деле, мы это учли движение частицы в целом, частица может иметь ещё внутренние состояния, связанные с её спином, тогда эта формула подправится, и мы напишем так:
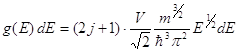
Этот множитель 2(j+1) – это число проекций спина на выбранную ось. Для электронов ![]() и 2j+1 = 2, то есть число состояний удваивается, тогда для идеального фермионного газа распределение по энергиям выглядит так:
и 2j+1 = 2, то есть число состояний удваивается, тогда для идеального фермионного газа распределение по энергиям выглядит так:
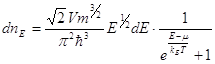
Такой множитель запоминать это безумие, важно, что функция распределения (что вы должны помнить, придя на экзамен)
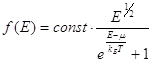
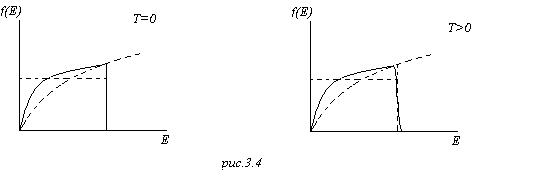 |
На что похожа эта функция?
![]()
Интеграл 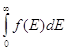 должен равняться полному числу частиц N. Для фермионного газа
должен равняться полному числу частиц N. Для фермионного газа 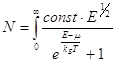 , если этот интеграл взять, можно определить
, если этот интеграл взять, можно определить ![]() .
.
0 комментариев