Твёрдое тело. Решётка Браве. Обратная решётка

3. Твёрдое тело. Решётка Браве. Обратная решётка

Чем замечателен идеальный кристалл? Тем, что в нём возможны сдвиги, при которых вся эта структура переходит в себя (в узлах могут быть сложные группы атомов, они тоже переходят в себя).

Кристалл – это трёхмерная структура, три вектора , не лежащих, естественно, в одной плоскости, такие, что при сдвиге на вектор , где n₁, n₂, n₃ – любые целые числа, структура переходит в себя, задают элементарную ячейку кристалла, объём этой ячейки равен

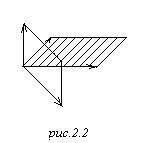Данной решётке ставится в соответствие обратная решётка  с такими условиями: . Объём ячейки обратной решётки из геометрических соображений будет равен .

Симметрия кристалла позволяет получить важную теорему Блоха: волновые функции стационарных состояний электронов в твёрдом теле имеют вид , при этом пространственная функция  обладает таким свойством периодичности: .

Что эта волновая функция из себя представляет в одномерном случае? Функция  для частицы в пустом пространстве это плоская волна, её амплитуда промодулирована вот такой пространственной функцией  с периодом решётки , амплитуда должна быть больше в местах нахождения атомов и меньше там, где их нет, то есть в промежутках.

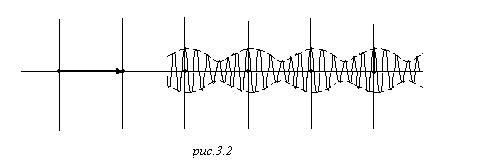
Вот примерно такая волновая функция электронов, она максимальна в окрестности атома, там плотность вероятности обнаружить электрон больше, но в общем-то она не равна нулю в межатомных промежутках. Это просто означает, что электроны в твёрдом теле уже не принадлежат атомам, каждый электрон – житель всей этой решётки, волновая функция электрона размазана по всему образцу. Понятно почему: атомы это соседние потенциальные ямы, разделённые потенциальным барьером, но есть туннельный эффект.

4. Зоны энергии

Электрон в твёрдом теле заведомо находится в связанном состоянии, согласно общим положениям квантовой теории его энергия должна квантоваться, то есть собственные значения гамильтониана должны быть дискретны. Мы увидим сейчас, как она квантуется. Напишем гамильтониан:

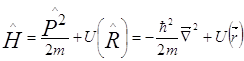
Потенциальная энергия выглядит, конечно, сложным образом: это потенциальные ямы в окрестности атомов, и её не только ядра создают, там и все электроны. Выражение для гамильтониана задать очень сложно, надо учитывать взаимодействие электронов между собой, взаимодействия с ядрами, взаимодействие ядер между собой…, но нам это не важно, нам важно одно – эта функция периодическая. Напишем уравнение на собственные значения гамильтониана, где функция имеет такой вид :

 или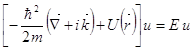

Для каждого  имеются значения , при которых это уравнение имеет решение, и тогда каждому  будут соответствовать собственные функции . Таким образом, стационарные состояния электронов в металле задаются двумя переменными вектором  и числом n, им отвечает функция  и энергия . Напишем окончательно так:

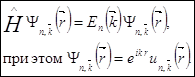
Вот главный результат от всей этой науки, и всё это добыто как следствие трансляционной инвариантности решётки (вся физика переходит в себя при сдвигах с определённым вектором ). Что мы получаем? Вот у нас энергетическая шкала E, возможные значения энергии определяются величинами . Фиксируем n, получаем какую-то функцию от , которая имеет минимальное значение и максимальное. n = 2, мы опять имеем полосу энергий, при каком-то значении  она минимальна, при каком-то значении  она максимальна. И в результате мы получаем, что энергия электронов в металле может лежать в пределах, так называемых, энергетических зон.

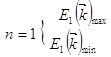
Для малых значений n эти зоны не перекрываются, но при больших значениях n они начинают перекрываться. Ещё более детальный анализ показывает, что имеются уровни энергий для электрона в атоме, когда эти атомы построятся в решётку, то эти уровни энергий расщепляются на зоны (рис. 4.2). Число уровней, на которые расщепляется начальный, равно 2N, где N – число атомов.

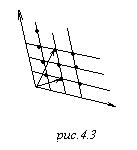Чтоб с этим кончить, какие значения принимает вектор ? В прошлый раз мы обсуждали понятие обратной решётки, вектор  имеет размерность обратной длины, значит вектор  это вектор, принадлежащий обратной решётке. Все значения вектора  в пределах элементарной ячейки отвечают определённым состоянию, если мы переходим в соседнюю ячейку, то там все состояния повторяются. Поэтому, если  – трансляционный вектор обратной решётки, то выполняются условия: , .