Функция f(x) имеет при x= с минимум, если ее значение при х=с меньше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с

2. Функция f(x) имеет при x= с минимум, если ее значение при х=с меньше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с.

Термины "максимум" и "минимум" объединяются в один общий для них термин "экстремум".

Значение аргумента, которое дает максимум (или минимум) функции, называется точкой максимума (минимума), или точкой экстремума.

Функция может иметь только максимум, например функция y = 60x— 2х2 (черт. 111), или только минимум, например функция у = 2х+72/x (черт. 112), или иметь

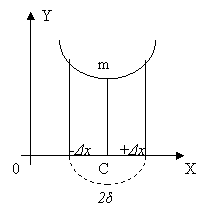
максимум и минимум, как, например, функция у = х3— — х2 — 8х+2 (черт. 108). Функция может иметь несколько максимумов и минимумов (черт. 113), причем в этом случае максимумы и минимумы чередуются. Функция может не иметь ни максимума, ни минимума. Например, функции у = х3, y = ctgx, y = ax не имеют ни максимума, ни минимума, так как при возрастании х от — ∞ до +∞ первая и третья функции возрастают, а вторая только убывает.

Максимум (минимум) функции может не быть наибольшим (наименьшим) значением ее. Так, изображенная на черт. 113 функция имеет в точке с. значение, большее максимумов с1М1 и с3М2, а в точке с0 значение, меньшее минимума c2m1, и c4m2, минимум c4m2 больше максимума с1М1. Максимум (минимум) функции в данной точке вообще есть наибольшее (наименьшее) значение функции по сравнению с ее значениями в точках, лежащих слева и справа от точки экстремума лишь в достаточной близости к ней.

Признаки существования экстремума

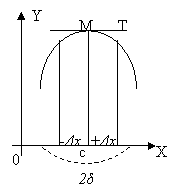
1°. Теорема (необходимый признак). Если в окрестности 2δ точки х=с:

1) функция f(х) дифференцируема, 2) значение х=с есть точка экстремума функции f(x), то ее производная в точке с равна нулю, m. e. f '(c) = 0.

Доказательство. Пусть для определенности х=c есть точка максимума (черт. 111). Представим значения независимого переменного х левой полуокрестности точки с в виде с — Δx:, а правой в виде с+ Δx, где 0< Δx < δ. Значение функции f(x) в точке с есть f(c), в левой полуокрестности оно равно f(с — Δx), а в правой f(c + Δx). Значения f(x) в окрестности 2δ точки с поставлены, таким образом, в зависимость от значений Δx, причем значение х = с -/+ Δx неограниченно приближается к числу с, если Δx стремится к нулю.

По определению максимума функции:

f(c- Δx)<f(c) и f(c + Δx)<f(c).

Отсюда:

f(c-Δx)-f(c)<0 и f(c + Δx)-f(с)<0.

Левые части неравенств выражают приращение функции в точке х = с при изменении аргумента соответственно на — Δx и + Δx. Составив отношение приращения функции к приращению аргумента, получаем:

lim ((f(c - Δx)-f(c))/(—Δx)) = f‘(c) и lim ((f(c + Δx)-f(c))/(+Δx)) = f‘(c).  - Δx→0 + Δx→0

(f(c —Δx)—f(с))/(-Δx))>0 (1); (f(с + Δx)—f(с)/(+Δx))<0 (2) Оба отношения (1) и (2) имеют один и тот же предел при Δx → 0, так как по условно функция f(x) имеет в точке с определенную произвольную:

Из неравенства (1) следует, что f '(с) либо положительна, либо равна нулю, а неравенство (2) показывает, что f '(с) не может быть положительной. Следовательно,

f‘(c) = 0,

что и требовалось доказать.

2°. Теорема (достаточный признак). Если в окрестности 2δ точки x = с:

1) функция f(x) непрерывна,

2) ее производная, f '(х), слева от точки х = с положительна, а справа отрицательна, то значение х = с есть точка максимума функции.

lim f(c - Δx) = f(c) и lim f(c + Δx) = f(c).  - Δx→0 + Δx→0

Доказательство. Данная функция непрерывна в точке c, поэтому число f(с) есть общий предел для f(c — Δx) и f(c+Δx) при Δx → 0 (как и в предыдущей теореме, здесь и в последующем 0 < Δx< δ):

Данная функция f(x) в левой полуокрестности точки с — возрастающая, так как ее производная слева от точки с положительна, а в правой полуокрестности — убывающая, так как ее производная справа от точки с отрицательна (черт.), и вследствие этого ее значения

f(c —Δx) и f(c+Δx)

возрастают при стремлении Δx к нулю (по определению убывающей функции, меньшему значению аргумента отвечает большее значение функции, т. е. при x1>x2 f(x1)<f(x2)).

Другими словами, как f(c — Δx), так и f(c+Δx) приближаются к своему пределу f(с) так, что для каждого значения Δx ≠ 0:

f(c - Δx) < f(c) и f(c + Δx) < f(c).

Но в таком случае f(c) есть максимум функции f(x) в точке х = с.

3°. Так же можно доказать, что если в окрестности 2δ точки х = с:

1) функция f(x) непрерывна, 2) производная f '(x) слева от точки х = с отрицательна, а справа положительна, то значение х = с есть точка минимума функции (черт.).

4°. Как в точке максимума, так и в точке минимума производная равна нулю (1°). Обратное неверно. Функция может не иметь ни максимума, ни минимума в точке, в которой производная равна нулю.

Например, функция у = х3 имеет в точке x =0 производную, равную нулю. Однако в точке х = 0 нет ни максимума, ни минимума, функция у = х3 при всех значениях х, в том числе и при x = 0, возрастает. Отсюда, в точке х=с функция f(x) не имеет на максимума, ни минимума, если при х = с ее производная равна нулю и имеет один и тот же знак как слева, так и справа от точки х = с.

5°. Определение. Значения аргумента х, при которых производная f '(х) равна нулю, называются стационарными точками.

Касательная в стационарных точках параллельна оси Ох. В окрестности точки максимума касательная составляет с осью абсцисс острый угол, если точка лежит слева от точки максимума, и тупой угол, если справа от нее (черт.). В случае минимума, напротив, касательная составляет с осью абсцисс тупой угол, если точка находится слева от точки минимума, и острый, если справа от нее (черт.).

Правило нахождения экстремума

1°. Чтобы найти экстремум функции, надо:

1) найти производную данной функции;

2) приравнять производную нулю и решить полученное уравнение; из полученных корней отобрать действительные и расположить их (для удобства) по их величине от меньшего к большему; в том случае, когда все корни оказываются мнимыми, данная функция не имеет экстремума;

3) определить знак производной в каждом из промежутков, отграниченных стационарными точками;

4) если производная положительна в промежутке, лежащем слева от данной стационарной точки, и отрицательна в промежутке, лежащем справа от нес, то данная точка есть точка максимума функции, если же производная отрицательна слева и положительна справа от данной стационарной точки, то данная точка есть точка минимума функции; если производная имеет один и тот же знак как слева, так и справа от стационарной тонки, то в этой точке нет ни максимума, ни минимума, функции;

5) затенить в данном выражении функции аргумент значением, которое дает максимум или минимум функции; получим значение соответственно максимума или минимума функции.

Если функция имеет точки разрыва, то эти точки должны быть включены в число стационарных точек, разбивающих Ох на промежутки, в которых определяется знак производной.

Нахождение экстремума при помощи второй производной

1°. Лемма. Если при х = с производная положительна (или отрицательна), то в достаточно малой окрестности точки х = с приращение функции и приращение аргумента в точке с имеют одинаковые (или разные) знаки.

lim (∆y/∆x)>0. ∆x→0

Доказательство от противного. Пусть для определенности f '(c)>0, т. е.

Предположим, что при стремлении ∆x к нулю приращения ∆y и ∆x имеют разные знаки. Тогда отношение ∆y/∆x отрицательно и его предел

f '(c) ≤ 0,

что противоречит условию.

Так же доказывается и вторая часть леммы.

2°. Теорема. Если при х = с первая производная функции f(x) равна нулю, f '(c)=0, а вторая производная положительна, f "(c)>0, то в точке х = с функция f(x) имеет минимум;

если же вторая производная отрицательна, f "(с) < 0, то в точке х = с функция f(x) имеет максимум.

f ’’(c) = lim ((f’(c + ∆x)-f ’(c))/∆x)>0. ∆x→0

Доказательство. Вторая производная по отношению к первой производной является тем же, чем первая производная по отношению к данной функции, т. е.

Согласно лемме, если при х = с производная (в данном случае вторая) положительна, то в достаточно малой окрестности 2δ точки с приращение функции (в данном случае первой производной) имеет тот же знак, что и приращение аргумента. Слева от точки с приращение аргумента отрицательно, значит, и приращение функции отрицательно, т.е.

f '(c — ∆x)—f(c)<0, (0 < ∆x < δ).

Отсюда:

f '(c-∆x)<f '(c) = 0. (1).

Справа от точки с приращение аргумента положительно, т. е.

f '(c +∆x)-f '(c)>0.

Отсюда:

f '(c + ∆x)>f '(c) = 0. (2)

Получили: первая производная функции f(x) слева от точки с отрицательна (1), а справа положительна (2). Значит, в точке х = с функция f(x) имеет минимум, как это и требовалось доказать.

Так же доказывается теорема и в случае f "(с)<0.

3°. Доказанная теорема определяет второй способ нахождения экстремума. Он отличается от первого тем, что третья и четвертая операции первого способа заменяются: а) нахождением второй производной и б) определением ее знака в стационарной точке. Результат исследования можно выразить так:

Если знак числа f "(с),	то при х = с f(x) имеет
плюс минус	минимум максимум

Если f '(с) = 0, то исследование функции на максимум и минимум надо провести первым способом.

4°. Пример 1. Исследовать вторым способом на максимум и минимум функцию: у = 5 — х2 — х3 — x4/4.

Решение. 1. Находим первую производную:

y ' = - 2х - Зx2 — x3

2. Приравниваем первую производную нулю и решаем полученное уравнение:

— 2x — Зx2 — x3 = 0, или x(x2+3х+2) = 0,

отсюда x = 0 или x2+ 3х + 2 = 0.

Решая квадратное уравнение x2 + 3х + 2 = 0, получаем:

x = (-3 + 1)/2.

Стационарных точек три: x1 = — 2, x2 = — 1 и х3 = 0.

3. Находим вторую производную:

у" = — 2 - бx — Зx2.

4. Определяем знак второй производной, заменяя х его значением сначала в первой, затем во второй и потом в третьей стационарной

точке:

при х = — 2 у'' = — 2 — 6(— 2) — 3(— 2)2 = — 2, при х = — 1 у" = — 2 — 6(— 1) — 3(— l)2 = + 1, при x = 0 у" = — 2.

Следовательно, данная функция имеет минимум при х = —1 и максимум при х = — 2 и при х =0,

Пример 2, Исследовать на максимум и минимум функцию: у = х4.

Решение: 1) y' = 4x3;

2) 4х3 = 0; х = 0;

3) y" = 12x2;

4) при х = 0 y" = 0.

Так как оказалось, что вторая производная равна нулю, то исследование ведем первым способом: при х < 0 у' = 4x3 < 0, а при х > 0 у' = 4x3 > 0. Следовательно, функция у = х4 имеет минимум в точке x = 0.

5°. Второй способ нахождения экстремума имеет смысл применять в том случае, когда вторая производная отыскивается просто; если же дифференцирование сопровождается трудными преобразованиями и не упрощает выражение первой производной, то первый способ может быстрее привести к цели.

Направление вогнутости кривой

Пусть две точки M1 и M2 имеют одну и ту же абсциссу. Если при этом ордината точки M1 более (менее) ординаты точки M2, то говорят, что точка M1 лежит выше (ниже) точки M2. Говорят также, что в промежутке а<х<b линия y = f(x) лежит выше (ниже) линии у=φ(х), если в этом промежутке каждая точка первой линии лежит выше (ниже) соответствующей ей точки второй линии, т. е. если

f(x)> φ(x) [или f(x)< φ(x)].

Определение. В промежутке а < х < b кривая— график дифференцируемой функции y=f(x) — называется вогнутой вверх (вниз), если она лежит выше (ниже) касательной в любой точке данного промежутка.

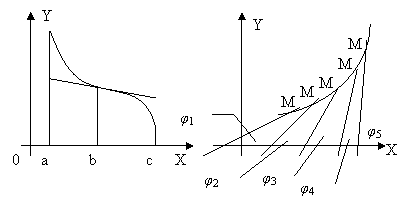Кривая, изображенная на черт., является вогнутой, вверх в промежутке а < х < b и вогнутой вниз в промежутке b < х < с.

2°. В более подробных курсах анализа доказывается, что если производная f '(х) — возрастающая (убывающая) функция в промежутке а < х < b, то кривая y=f(х) является вогнутой вверх (вниз) в этом промежутке.

Чтобы уяснить эту теорему, наметим на оси Ох (черт.)

произвольно ряд точек и проведем через каждую из них

прямую так, чтоб и угловом коэффициент прямой возрастал с возрастанием абсциссы намеченных точек; затем, приняв эти прямые за касательные к некоторой кривой линии [tgφ = f '(x)], построим эту кривую линию. Мы видим, что она может лежать только выше каждой из проведенных касательных.

3°. Достаточный признак вогнутости вверх (вниз). Если в промежутке а<х<b вторая производная f ''(x) положительна (отрицательна), за исключением отдельных точек, в которых она равна нулю, то кривая у=f(х) в этом промежутке вогнута вверх (вниз).

Действительно, если в промежутке а<х<b вторая производная f "(x), например, положительна, за исключением отдельных точек, в которых она равна нулю, то первая производная f '(х)—возрастающая функция, а кривая y = f(x), согласно предыдущему, является вогнутой вверх.

Если f "(x) = 0 не в отдельных точках, а в некотором промежутке, то в этом промежутке f '(x) — постоянная функция, a f(x) — линейная функция, график ее — прямая линия, и говорить о вогнутости не имеет смысла.

Точки перегиба

1°. Определение, Если в некоторой окрестности точки х = с кривая —график дифференцируемой функции y = f(x) — имеет слева и справа от точки х = с вогнутости противоположного направления, то значение х = с называется точкой перегиба.

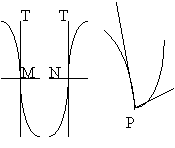Точку М кривой (черт.), абсцисса которой х = с, называют также точкой перегиба, она отделяет дугу кривой, вогнутую вверх, от дуги, вогнутой вниз. Точкой перегиба может быть только та точка, в которой к кривой имеется касательная. В окрестности точки перегиба кривая лежит по обе стороны от касательной: выше и ниже ее. Заметим, что она расположена также по обе стороны от нормали. Но такая точка, как Р (черт.), в которой единственной касательной не имеется, точкой перегиба не является.

2°. Так как слева и справа от точки перегиба х = с вогнутости кривой y=f(x) разного направления, то вторая производная f "(x) имеет слева и справа от точки х = с разные знаки или равна нулю. Полагая вторую производную непрерывной и окрестности точки х = с, заключаем, что в точке перегиба она равна нулю, т. е.

f(c) = 0.

3°. Отсюда следует правило нахождения точек перегиба:

1) найти вторую производную данной функции;

2) приравнять ее нулю и решить полученное уравнение (или найти те значения х, при которых производная теряет числовой смысл), из полученных корней отобрать действительные и расположить их no величине от меньшего к большему;

3) определить знак второй производной в каждом, из промежутков, отграниченных полученными корнями;

4) если при этом в двух промежутках, отграниченных исследуемой точкой, знаки второй производной окажутся разными, то имеется точка перегиба, если одинаковыми, то точки перегиба нет.

4°. Примеры. Найти точки перегиба и определить промежутки вогнутости вверх и вниз кривых:

1) у = lп х.

Р е ш е н и е. Находим вторую производную:

y '=1/x; y ''= -1/x2.

При всяком значении x = (0 < х <+∞) у" отрицательна. Значит, логарифмика точек перегиба не имеет и обращена вогнутостью вниз.

2) у = sin x.

Решение. Находим вторую производную:

y' =cos x, y'' = -sin x.

Полагая - sin x = 0, находим, что x = kπ, где k - целое число.

Если 0 < x< π, то sin x положителен и y '' отрицательна, если же π < x< 2π, то sin x отрицателен и y'' положительна и т. д. Значит, синусоида имеет точки перегиба 0, π, 2π,...

В первом промежутке 0 < x< π она обращена вогнутостью вниз, во втором - вогнутостью вверх и т. д.

Механическое значение второй производной

Предположим, что точка движется прямолинейно и пройденный ею путь определяется уравнением s = f(t), где t время. Скорость v в момент времени t есть производная от пути по времени, т. е.

v=ds/dt.

Скорость изменения скорости в момент времени t есть ускорение а,

a=(v)' = (ds/dt)' = (d2s/dt2).

Вторая производная от пути по времени есть ускорение прямолинейного движения в данный момент времени.

Пример. Прямолинейное движение точки совершается по закону:

s = (t3 — 2) м.

Определить ускорение в момент t = 10 сек.

Решение. Ускорение а = d2s/dt2.

Дифференцируя функцию s=t3 — 2, находим d2s/dt2 =6t

Следовательно,

a = 6t = 6*10 = 60; a = 60 мсек2.

2°. Если движение неравномерное, то сила F, производящая его, непостоянна, каждому моменту времени t соответствует определенное значение действующей силы F, и сила, таким образом, есть функция времени t, F=f(t).

По закону Ньютона, в каждый момент времени действующая сила F равна произведению массы т на ускорение а, т. е.

F=ma, или f(t) = ma.

При прямолинейном движении a =d2s/dt2, поэтому

f(t) = m*d2s/dt2.

Зная уравнение прямолинейного движения, можно дифференцированием найти значение действующей силы в каждый момент времени.

Пример. Определить силу, под действием которой материальная точка совершает прямолинейные колебания по закону

s = А*sin(ωt + ω0).

Решение. f(f) = m*d2s/dt2, поэтому находим вторую производную функции:

s = А*sin(ωt + ω0), ds/dt = А*cos(ωt+ω0)* ω,

d2s/dt2=— А*sin (ωt + ω0)* ω2 = — s*ω2 = — ω2s; f(t) = — mω2s,

т. е. рассматриваемые колебания совершаются под действием силы, пропорциональной перемещению s и направленной в противоположную сторону.

Дифференциал Сравнение бесконечно малых

1°. Составим отношение бесконечно малых, приближающихся к нулю по различным законам, так что каждому рассматриваемому моменту приближения к нулю одной из бесконечно малых отвечает определенное значение каждой из рассматриваемых бесконечно малых. Например, пусть в те моменты приближения к нулю, когда значения α = 10;1; 0.1; 0,01 и т.д.;

значения β =1000; 1; 0,001; 0,000001 и т.д.

Отношение β/α =100; 1; 0, 01; 0, 0001 и т.д., т.е.

значение отношения бесконечно малых не остается неизменным в процессе приближения их к нулю. Отношение бесконечно малых, таким образом,—величина переменная, и у нее может существовать предел, конечный (равный нулю, как в примере, или отличный от нуля) или бесконечный, а может предела и не существовать.

2°. Определения: 1) β называется бесконечно малой высшего порядка малости, чем α, если предел отношения β/α равен нулю, т. е. если

limβ/α =0;

2) β называется бесконечно малой низшего порядка малости, чем α, если

limβ/α = ∞;

3) β и α называются бесконечно малыми одинакового порядка малости, если предел их отношения есть число k, отличное от нуля, т. е. если

limβ/α = k, где k ≠ 0 и k ≠ ∞

4) β и α называются несравнимыми бесконечно малыми, если предела их отношения не существует.

3°. Примеры. 1. В рассмотренном выше примере limβ/α = 0, β высшего порядка малости, чем α, a limα/β = ∞ и α низшего порядка, чем β.

lim (β/α) = lim (1+x) =2. х→1

2. α =1—х и β=1— x2 —бесконечно малые, если х→1. Отношение β/α=(1- x2)/(1-x) = 1+x.

Значит, 1—х и 1—x2 —бесконечно малые одинакового порядка малости при х→1.