Навигация
2. О числе решений ЛДУ.
Теорема 1. При взаимно простых коэффициентах 
диофантово уравнение
имеет решение в целых числах.
Доказательство. Обозначим через 
множество тех положительных чисел 
, для которых уравнение
имеет решение в целых числах. , очевидно, не пусто, так как при заданных , можно подобрать целые значения 
, такие, чтобы 
было положительным числом.
В множестве существует наименьшее число ( – подмножество натуральных чисел), которое мы обозначим через 
Обозначим через 
- целые числа, такие, что
.
Пусть 
, где 
; тогда
.
Мы подобрали целые значения: 
, 
,…, 
, такие, что 
, но , а - наименьшее положительное число в , т. е. 
не может быть положительным, 
, 
, 
.
Аналогично получаем: 
,…,
.
Мы видим, что – общий делитель чисел , следовательно, поскольку 
, 
, 
, 
, то уравнение разрешимо в целых числах.
Теорема 2. Пусть - наибольший общий делитель коэффициентов . Диофантово уравнение имеет решение тогда и только тогда, когда 
. Число решений такого уравнения равно либо нулю, либо бесконечности.
Докажем последовательно все три утверждения теоремы.
1). Пусть . Для уравнения
,
где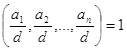 
, существуют целые числа: 
удовлетворяющие ему. Т.е. такие, что
.
Тогда
т. е. 
- решение уравнения.
2). Пусть теперь не делит . Тогда левая часть уравнения при любых целых делится на , а правая на не делиться, так что равенство при целых значениях невозможно.
3). Если 
- упорядоченная n-ка чисел, удовлетворяющий уравнению, то например, все n-ки
при 
также удовлетворяют этому уравнению и, таким образом, у нас либо совсем не будет решений, либо их будет бесконечное множество.
Если хоть одна пара коэффициентов взаимно простая, то , и уравнение имеет бесчисленное множество решений.
3. Нахождение решений для некоторых частных случаев ЛДУ.
3.1. ЛДУ c одной неизвестной.
Рассмотрим линейное уравнение с одной неизвестной, т.е. уравнение вида
Ясно, что решением данного уравнения будет 
, и решение будет целым числом только в том случае, когда 
.
Похожие работы
... . Общая теория решения Диофантовых уравнений 1-й степени была создана в 17 веке. К началу 19 века трудами П. Ферма , Дж. Виллса, Л. Эйлера, Ж. Лагранжа и К. Гауса в основном было исследовано Диофантово уравнение вида ax²+bxy+cy²+dx+ey+f=0, где а,b,c,d,e,f- целые числа, то есть общее неоднородное уравнение 2-й степени с двумя неизвестными. Перейдем теперь к одной из самых ...
... этом промежутке неравенство (11) также не имеет решений. Итак, неравенство (11) решений не имеет. Ответ: Ø. 3 НЕКОТОРЫЕ ИСКУССТВЕННЫЕ СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ Существуют и другие нестандартные методы решения уравнений и неравенств, помимо использования свойств функции. Данная глава посвящена дополнительным методам решения. 3.1 Умножение уравнения на функцию Иногда решение ...
... Z 12 30 (15) При рассмотрении вопроса о Пифагоровых тройках не было целью составление таблиц этих троек. Ибо целью этой статьи является показ возможностей алгоритма решения Диофантовых уравнений. Решение уравнения Каталана Уравнение данного вида получается при попытке решения гипотезы Биля. Поэтому решение данного уравнения является как бы леммой гипотезы Биля. Ответ будет ...
... из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна. Следствие 3. . Доказательство. Пусть . Тогда, по лемме 1 пункта 13 имеем: . 5 Китайская теорема об остатках В этом пункте детально рассмотрим только сравнения первой степени вида ax b(mod m), оставив более высокие степени на съедение следующим ...
0 комментариев