Навигация
3.2. ЛДУ с двумя неизвестными.
Рассмотрим теперь линейное уравнение с двумя неизвестными
, 
.
Покажем несколько алгоритмов для нахождения решения.
Способ 1.
Пусть 
Рассмотрим два случая:
а). 
не делится на 
. В этом случае решений нет по теореме 2.
б). делится на , поделим на .
;
.
Таким образом получили новое ЛДУ, с тем же множеством решений, но уже со взаимно-простыми коэффициентами. Поэтому далее мы будем рассматривать именно такие уравнения.
Рассмотрим , 
.
, перейдем к сравнению,
.
Т.к. , то сравнение имеет единственное решение 
.
; подставим в уравнение.
;
;
, причем 
.
Обозначим 
.
Тогда общее решение можно найти по формулам: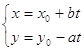 
, где 
.
Пример. 
, 
.
Найдем решение сравнения 
;
;
, т.е. 
.
;
Получили общее решение: 
, где .
Способ 2.
Рассмотрим еще один способ нахождения решения ЛДУ с двумя неизвестными, а для этого рассмотрим уравнение вида 
. Уравнения такого вида называются линейными однородными диофантовыми уравнениями (ЛОДУ). Выражая неизвестную 
, через неизвестную 
приходим к 
. Так как x должен быть целым числом, то
, где 
- произвольное целое число. Значит
. Решениями ЛОДУ являются n-ки вида 
, где . Множество всех таких n-ок называется общим решением ЛОДУ, любая же конкретная пара из этого множества называется частным решением.
Рассмотрим теперь уравнение , . Пусть n-ка
его частное решение, а множество n-ок общее решение соответствующего ЛОДУ. Докажем предложение.
Общее решение ЛДУ , задается уравнениями 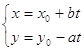, где .
Доказательство. То, что правые части указанных в формулировке теоремы равенств действительно являются решениями, проверяется их непосредственной подстановкой в исходное уравнение. Покажем, что любое решение уравнения имеет именно такой вид, какой указан в формулировке предложения. Пусть 
- какое-нибудь решение уравнения . Тогда 
, но ведь и 
. Вычтем из первого равенства второе и получим:
- однородное уравнение. Пишем сразу общее решение: 
, откуда получаем:
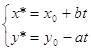. Доказательство завершено.
Встает вопрос о нахождении частного решения ЛДУ.
По теореме о линейном разложении НОД, это означает, что найдутся такие 
и 
из множества целых чисел, что 
, причем эти и мы легко умеем находить с помощью алгоритма Евклида. Умножим теперь равенство на и получим: 
, т.е.
, 
.
Таким образом, для нахождения общего решения находим общее решение ЛОДУ, частное решение ЛДУ и их складываем.
Замечание: особенно этот способ удобен, когда 
или 
. Если, например, , 
, тогда n-ка 
, очевидно, будет частным решением ЛДУ. Можно сразу выписывать общее решение.
Пример. , .
Найдем частное решение. Используем алгоритм Евклида.
;
Получаем линейное разложение НОД:
, т.е 
.
, 
Получили общее решени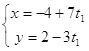е: 
, где 
.
Как видим, получили решение, не совпадающее с решением, найденным первым способом.
Обозначим 
и получим , т.е эти решения равносильны.
Способ 3.
Еще один способ опирается на теорему:
Пусть - произвольное решение диофантова уравнения
, , тогда
множество решений уравнения в целых числах совпадает с множеством пар 
, где 
, 
, где t – любое целое число.
Доказательство этого несложного факта можно найти, например, в книге Бухштаба [2, стр. 114].
Опять же частное решение можно легко отыскать с помощью алгоритма Евклида.
Похожие работы
... . Общая теория решения Диофантовых уравнений 1-й степени была создана в 17 веке. К началу 19 века трудами П. Ферма , Дж. Виллса, Л. Эйлера, Ж. Лагранжа и К. Гауса в основном было исследовано Диофантово уравнение вида ax²+bxy+cy²+dx+ey+f=0, где а,b,c,d,e,f- целые числа, то есть общее неоднородное уравнение 2-й степени с двумя неизвестными. Перейдем теперь к одной из самых ...
... этом промежутке неравенство (11) также не имеет решений. Итак, неравенство (11) решений не имеет. Ответ: Ø. 3 НЕКОТОРЫЕ ИСКУССТВЕННЫЕ СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ Существуют и другие нестандартные методы решения уравнений и неравенств, помимо использования свойств функции. Данная глава посвящена дополнительным методам решения. 3.1 Умножение уравнения на функцию Иногда решение ...
... Z 12 30 (15) При рассмотрении вопроса о Пифагоровых тройках не было целью составление таблиц этих троек. Ибо целью этой статьи является показ возможностей алгоритма решения Диофантовых уравнений. Решение уравнения Каталана Уравнение данного вида получается при попытке решения гипотезы Биля. Поэтому решение данного уравнения является как бы леммой гипотезы Биля. Ответ будет ...
... из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна. Следствие 3. . Доказательство. Пусть . Тогда, по лемме 1 пункта 13 имеем: . 5 Китайская теорема об остатках В этом пункте детально рассмотрим только сравнения первой степени вида ax b(mod m), оставив более высокие степени на съедение следующим ...
0 комментариев