Навигация
Нахождение решений произвольного ЛДУ
14606
знаков
0
таблиц
1
изображение
4. Нахождение решений произвольного ЛДУ.
Перейдем теперь к решению ЛДУ с 
неизвестных, т. е. уравнений вида
где все коэффициенты и неизвестные – целые числа и хотя бы одно 
. Для существования решения по теореме 2, необходимо, чтобы
Положив
перейдем к равносильному уравнению
(*),
где
. Пусть
, 
- два ненулевых числа, таких, что 
Для определенности предположим, что
, 
Разделив с остатком на , получим представление 
. Заменив на 
в уравнении (*), приведем его к виду
Перепишем это уравнение в виде
(**)
где
, 
.
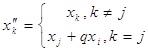Очевидно, что решения уравнения (*) и (**) связаны между собой взаимно однозначным соответствием и, таким образом, решив уравнение (**), несложно найти все решения уравнения (*). С другой стороны отметим, что
Отметим также, что
Следовательно, за конечное число шагов уравнение (*) приведется к виду
(***)
где числа 
(i = 1,...,n), которые не равны нулю, равны между собой по абсолютной величине. Из соотношения 
следует, что числа могут принимать только значения 0,±1, причем не все из них равны нулю. Предположим, для определенности, 
. Тогда уравнение (***) имеет следующее решение:
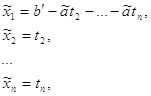
где t2, t3, ..., tn - произвольные целые числа. Отсюда, учитывая проведенные замены, получается и решение уравнения (*). Отметим, что при получении решения уравнения (***) использовался лишь факт, что 
, поэтому, при выполнении алгоритма можно остановиться на том шаге, когда хотя бы один из коэффициентов станет равным ±1.
5. Примеры решений задач.
1). Решить в целых числах уравнение
4x - 6y + 11z = 7, (4,6,11)=1.
Разделив с остатком -6 на 4, получим -6 = 4(-2) + 2. Представим исходное уравнение в виде
4(x - 2y) + 2y + 11z = 7.
После замены x = x - 2y это уравнение запишется следующим образом
4x + 2y + 11z = 7.
Учитывая, что 11 = 2·5 + 1, преобразуем последнее уравнение:
4x + 2(y + 5z) + z = 7.
Положив y = y + 5z, получим
4x + 2y + z = 7.
Это уравнение имеет следующее решение: x, y - произвольные целые числа, z = 7 - 4x - 2y.
Следовательно y = y - 5z = 20x + 11y - 35, x = x + 2y = 41x + 22y - 70.
Таким образом, решение исходного уравнения имеет вид
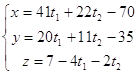, где
, 
- произвольные целые числа.
2). Решить в целых числах уравнение
Разделим 5 на -4 с «остатком», 
, преобразуем исходное уравнение к виду
.
Заменив 
получим 
, следовательно
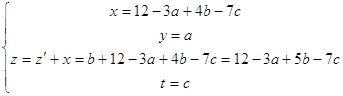, является решением данного ЛДУ.
Список литературы
Башмакова, И.Г. Диофант и диофантовы уравнения [Текст]. – М.: «Наука», 1972 г. - 68 с.
Бухштаб, А. А. Теория чисел [Текст]. - М.: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1960. - 378 с.
Виноградов, И.М. Основы теории чисел: Учебное пособие. 11-е изд. [Текст]. – СПб.: Издательство «Лань», 2006. - 176 с.
Гаусс, Карл Фридрих Труды по теории чисел. Под общей ред. Виноградова И.М. [Текст] – М.: Изд. академических наук СССР, 1959 г. - 980 с.
Гельфонд, А.О. Решение уравнений в целых числах. Популярные лекции по математике, вып. [Текст]. М.: «Гостехиздат», 1957 г. - 66 с.
Давенпорт, Г. Введение в теорию чисел [Текст]: Пер. с английского Мороза Б.З. под ред. Линника Ю.В. – М.: «Наука», 1965 г. - 176 с.
Матисеевич, Ю.В. Десятая проблема Гильберта [Текст]. - М.: «Физматлит», 1973 г. - 224 с.
Михелович, Ш.Х. Теория чисел [Текст]. – М.: «Высшая школа», 1962 г. - 260 с.
Соловьев, Ю. Неопределенные уравнения первой степени [Текст]: Квант, 1992 г., №4.
Стройк, Д.Я. Краткий очерк истории математики [Текст]. – М.: «Наука», 1990 г. - 256 с.
Для подготовки данной работы были использованы материалы с сайта http://revolution./
Похожие работы
... . Общая теория решения Диофантовых уравнений 1-й степени была создана в 17 веке. К началу 19 века трудами П. Ферма , Дж. Виллса, Л. Эйлера, Ж. Лагранжа и К. Гауса в основном было исследовано Диофантово уравнение вида ax²+bxy+cy²+dx+ey+f=0, где а,b,c,d,e,f- целые числа, то есть общее неоднородное уравнение 2-й степени с двумя неизвестными. Перейдем теперь к одной из самых ...
... этом промежутке неравенство (11) также не имеет решений. Итак, неравенство (11) решений не имеет. Ответ: Ø. 3 НЕКОТОРЫЕ ИСКУССТВЕННЫЕ СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ Существуют и другие нестандартные методы решения уравнений и неравенств, помимо использования свойств функции. Данная глава посвящена дополнительным методам решения. 3.1 Умножение уравнения на функцию Иногда решение ...
... Z 12 30 (15) При рассмотрении вопроса о Пифагоровых тройках не было целью составление таблиц этих троек. Ибо целью этой статьи является показ возможностей алгоритма решения Диофантовых уравнений. Решение уравнения Каталана Уравнение данного вида получается при попытке решения гипотезы Биля. Поэтому решение данного уравнения является как бы леммой гипотезы Биля. Ответ будет ...
... из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна. Следствие 3. . Доказательство. Пусть . Тогда, по лемме 1 пункта 13 имеем: . 5 Китайская теорема об остатках В этом пункте детально рассмотрим только сравнения первой степени вида ax b(mod m), оставив более высокие степени на съедение следующим ...
0 комментариев