Навигация
Докажите, что в результате второго преобразования получается разбиение с различными частями
3. Докажите, что в результате второго преобразования получается разбиение с различными частями.
4. Докажите, что если сначала выполнить преобразование Глэйшера, а затем обратное, то получится исходное разбиение.
Существует другое, не менее интересное и совершенно неожиданное доказательство теоремы Эйлера, принадлежащее американскому математику XIX века Дж. Сильвестру. Вот конструкция Сильвестра: пусть имеется разбиение числа n на нечётные части: (2k1+1, 2k2+1, ..., (2kq+1), где k1 ≥ k2 ≥ ... ≥ kq. На листе клетчатой бумаги в некотором её узле поставим точку x1. Справа от x1, поставим в узлах k1 точек и столько же точек поставим в узлах, расположенных под точкой x1. Затем проделаем то же самое с числом k2, взяв в качестве исходной точку x2, расположенную в следующем за точкой x1 по диагонали направо вниз узле, и т.д., пока не дойдём до числа kq.
Например, разбиению на нечётные части (9, 9, 5, 1, 1) числа 25 будет отвечать картинка, изображённая на рис. 1.
|
Рис. 1. |
Рис. 2. |
Она состоит из симметричных относительно диагонали уголков, так что в самом верхнем уголке 2k1+1 точек, в следующем 2k2+1 точек и т.д., а всего точек будет n. Теперь проведём на той же картинке линии так, как показано на рис. 2, подсчитаем количество точек на каждой из этих линий и образуем из полученных таким образом чисел разбиение. Оказывается, все части этого разбиения различны.
Упражнение 5. Докажите это утверждение.
В нашем примере получится разбиение (9, 6, 5, 4, 1). Подумайте, как построить по разбиению на различные части разбиение на нечётные, т.е. восстановить по такому разбиению исходную симметричную картинку.
Отступление: решение задачи М1065
В этом разделе используется более сложная техника, чем в остальной части статьи. При желании вы можете пробежать его, не вникая в детали, и продолжить чтение со следующего раздела. Итак, займёмся решением задачи М1065 из «Задачника «Кванта» (1987, № 9). Напомним её формулировку.
Будем рассматривать векторы (x, y) с целыми неотрицательными координатами, причём хотя бы одна из координат отлична от 0. Назовём такой вектор образующим, если |x–y| = 1.
а) Докажите, что рассматриваемый вектор (x, y) можно представить в виде суммы различных образующих (или он сам — образующий) тогда и только тогда, когда величина k(x, y) = x + y – (x–y)2 неотрицательна.
б) Докажите, что число N(x, y) различных (с точностью до порядка) представлений вектора (x, y) в виде суммы различных образующих зависит только от числа k = k(x, y). Найдите N(13, 18).
Решение задачи начнём с того, что найдём общий вид целочисленных решений неравенства k(x, y) ≥ 0. Числа x+y и x–y имеют одинаковую чётность, поэтому k(x, y) является чётным при любых целых x, y. Следовательно, для любого целого m≥0 достаточно найти целочисленные решения уравнения x + y – (x–y)2 = 2m. Положим x–y = q. Тогда x+y = 2m+q2. Из этих двух равенств немедленно получаем:
| (3) |
где q — любое целое число, а m ≥ 0.
Смысл чисел m и q станет более наглядным, если представлять себе векторы вида (3) при m=0 как точки с целыми координатами параболы k(x, y) = 0, лежащей в плоскости (x, y). (Вы понимаете, почему это парабола?) Тогда полученные нами целочисленные решения неравенства k(x, y) ≥ 0. показывают, что все точки с целыми координатами, лежащие на параболе k(x, y) = 0 и внутри неё, получаются сдвигами целых точек этой параболы на векторы (m, m) (рис. 3). Удобно считать, что число m (m=0, 1, 2, ...) — номер параболы, на которой лежит точка (x, y), a q = x–y = 0, ±1, ±2, ... — номер точки на этой параболе.
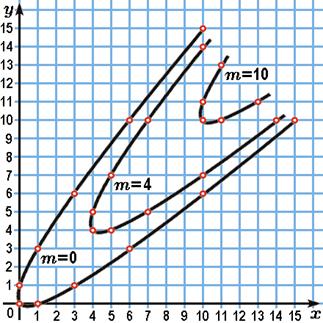
Рис. 3.
Поскольку условия задачи симметричны относительно перестановки координат векторов, достаточно доказать все утверждения для таких векторов (x, y), что x ≥ y, т.е. для векторов вида (3) с q ≥ 0.
Докажем достаточность условия в пункте а) задачи. По формуле суммы арифметической прогрессии
| 1 + 2 + ... + (q–1) + m + q = m + | q(q + 1) 2 | ; |
| 0 + 1 + ... + (q–2) + m + (q–1) = m + | q(q – 1) 2 | . |
Поэтому формулы
(x, y) = (1, 0) + (2, 1) + ... + (q–1, q–2) + (m+q, m+q–1) при q>0
и
(m, m) = (1, 0) + (m–1, m) при q=0, m>0
дают представления (x, y) в виде суммы различных образующих.
Доказать необходимость условия тоже несложно. Пусть
(x, y) = (r1, r1–1) + ... + (ra, ra–1) + (s1, s1+1) + ... + (sb, sb+1)
— представление вектора (x, y) с x ≥ y в виде суммы различных образующих, где
| r1 > r2 > ... > ra > 0, s1 > s2 > ... > sb ≥ 0. | (4) |
Для такого вектора
x = r1 + ... + ra + s1 + ... + sb,
y = r1 + ... + ra – a + s1 + ... + sb + b,
поэтому x–y = a–b. Положим q = x–y и
m = (r1–q) + (r2–(q–1)) + ... + (rq–1) + rq+1 + ... + ra + s1 + ... + sb =
| = x – | q(q + 1) 2 | = | x + y 2 | + | x – y 2 | – | q(q + 1) 2 | = | x + y 2 | – | q² 2 |
(здесь мы снова воспользовались формулой суммы арифметической прогрессии). Из неравенств (4) следует, что rq ≥ ra ≥ 1, rq–1 ≥ 2, rq–2 ≥ 3, ... и вообще rk ≥ q–k+1. Поэтому m ≥ 0, т.е. (x, y) — вектор вида (3), что и требовалось доказать.
В геометрических терминах утверждение б) означает, что число N(x, y) зависит лишь от номера m параболы и не зависит от номера q точки на параболе.
Пусть T(m, q) — множество представлений вектора (3) в виде суммы различных образующих и t(m, q) — число таких представлений. Задача будет решена, если мы докажем, что для любого целого q имеет место равенство t(m, q) = t(m, q–1) (это и значит, что t(m, q), а вместе с ним N(x, y), не зависит от q). Мы отождествили выше множество T(m, q) с множеством таких пар последовательностей, удовлетворяющих неравенствам (4), что
| r1 + ... + ra + s1 + ... + sb = m + | q(q + 1) 2 | при q = a–b. |
Такую пару мы будем записывать в виде (r1, ..., ra | s1, ..., sb).
Рассмотрим отображение φ множества T(m, q) в множество T(m, q–1), заданной формулой
| φ(r1, ..., ra | s1, ..., sb) = |
|
|
Упражнение 6. Проверьте, что φ(r1, ..., ra | s1, ..., sb) T(m, q–1).
Чтобы доказать, что φ — взаимно однозначное отображение, построим обратное отображение ψ: T(m, q–1) → T(m, q), прочитав правило, задающее φ, слева направо:
| ψ(r1, ..., ra | s1, ..., sb) = |
|
|
Построенные отображения взаимно обратны, поэтому φ — взаимно однозначное соответствие. Значит, t(m, q) = t(m, q–1), что и утверждалось.
Чтобы научиться вычислять значения N(x, y), установим связь между числами t(m, q) и p(m).
Утверждение: t(m, q) = p(m).
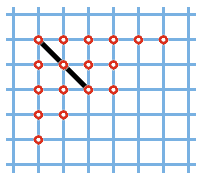
Рис. 4.
Мы уже знаем, что t(m, q) = t(m, 0), поэтому достаточно доказать, что t(m, 0) = p(m). Воспользуемся простым и полезным графическим средством, называемым диаграммой Юнга разбиения. Рассмотрим, например, разбиение (6, 4, 4, 2, 1). Его диаграмма Юнга изображена на рис. 4 (в первой строчке стоят 6 точек, во второй — 4, в третьей — 4, в четвёртой — 2, в пятой — 1). Всякое разбиение можно изобразить в виде диаграммы Юнга и по всякой диаграмме Юнга — записать разбиение.
Проведём на диаграмме Юнга диагональ — чёрная линия на рис. 4. Пусть r1 — число точек в первой строке, лежащих на диагонали и справа от неё, r2 — число точек второй строки, лежащих на диагонали и справа от неё, и т.д.; s1 — число точек первого столбца под диагональю, s2 — число точек второго столбца под диагональю и т.д. Поставим в соответствие диаграмме Юнга, изображающей разбиение числа m, пару последовательностей
(r1, r2, ... | s1, s2, ...),
r1 + r2 + ... + s1 + s2 + ... = m,
т.е. элемент множества T(m, 0). Например, диаграмме на рис. 4 соответствует пара (6, 3, 2 | 4, 2, 0). Зная пару последовательностей, можно легко восстановить диаграмму Юнга. Следовательно, мы установили взаимно однозначное соответствие между множеством разбиений и множеством T(m, 0). Утверждение доказано.
Теперь ничего не стоит ответить и на последний вопрос задачи — о значении N(13, 18). Поскольку 13 = 3+5·4/2, 18 = 3+6·5/2, точка (13, 18) лежит на третьей параболе. Значит, N(13, 18) = t(3, 0) = p(3) = 3.
Следующие упражнения — на применение диаграмм Юнга.
Упражнения
7. Число разбиений n не более чем с k частями, равно числу разбиений n с частями, не превосходящими k. Подсказка: отразите диаграмму Юнга относительно диагонали.
8. Число разбиений n с различными нечётными частями равно числу разбиений n, диаграмма Юнга которых симметрична относительно диагонали. Подсказка: вспомните соответствие Сильвестра.
Формула Гаусса–Якоби
Решая задачу М1065, мы проделали большую работу. Нельзя ли снова воспользоваться производящими функциями и извлечь из равенства t(m, q) = p(m) какое-нибудь красивое тождество?
N(x, y) — это число способов, которыми можно представить вектор (x, y) как сумму различных образующих вида (k, k–1) и (k–1, k). Рассуждая так же, как при выводе формулы производящей функции числа разбиений с различными частями, мы запишем производящую функцию для N(x, y) (это ряд от двух переменных u и v):
| ∞ | ∞ | ||
| ∏ | (1 + uk–1 vk)(1 + uk vk–1) = | ∑ | N(x, y)ux vy. |
| k=1 | x,y=0 |
Поскольку N(x, y) = t(m, q), где x = m + q(q+1)/2, y = m + q(q–1)/2, равенство можно продолжить:
| ∞ | ∞ | |||||
| = | ∑ | ∑ | t(m, q)um vm | uq(q+1)/2 vq(q–1)/2. | ||
| q=–∞ | m=0 |
Воспользуемся теперь тем, что t(m, q) = p(m) и продолжим равенство:
| ∞ | ∞ | |||||
| = | ∑ | ∑ | p(m)um vm | uq(q+1)/2 vq(q–1)/2. | ||
| q=–∞ | m=0 |
Ряд, стоящий в скобках, — производящая функция чисел разбиения p(m), которую мы знаем (формула (1)), поэтому продолжаем:
| ∞ | ∞ | |||
| = | ∏ | (1 – uk vk)–1 | ∑ | uq(q+1)/2 vq(q–1)/2. |
| k=1 | q=–∞ |
Теперь приравняем левую часть первого и правую часть последнего равенства, умножив обе части на ∏ (1–uk vk). Получим окончательный результат:
| ∞ | ∞ | ||
| ∏ | (1 + uk–1 vk)(1 + uk vk–1)(1 – uk vk) = | ∑ | uq(q+1)/2 vq(q–1)/2. |
| k=1 | q=–∞ |
Это тождество — цель наших преобразований. Оно называется формулой Гаусса–Якоби. Из этого замечательного тождества с двумя переменными можно получить много разных тождеств с одной переменной.
Упражнение 9. Подставьте в формулу Гаусса–Якоби u = –t, v = –t2 и получите пентагональную теорему Эйлера.
Теперь подставим в формулу Гаусса–Якоби u = v = – t. В левой части получится:
| ∞ | ∞ | ∞ | |||
| ∏ | (1 – t2k–1)2 (1 – t2k) = | ∏ | (1 – t2k–1) | ∏ | (1 – tk). |
| k=1 | k=1 | k=1 |
Заменяя произведение ∏ (1 – t2k–1) на ∏ (1 + tk)–1 по формуле (2), мы преобразуем левую часть в
| (1 – t)(1 – t2)(1 – t3) ... (1 + t)(1 + t2)(1 + t3) ... | . |
Правая часть формулы Гаусса–Якоби при подстановке u = v = – t превращается в
| ∞ | |
| ∑ | (–1)q² tq², |
| q=–∞ |
и мы получаем следующую формулу:
| (1 – t)(1 – t2)(1 – t3) ... (1 + t)(1 + t2)(1 + t3) ... | = 1 – 2t + 2t4 – 2t9 + 2t16 – ... |
Подстановка u = t, v = 1 в формулу Гаусса–Якоби аналогичным образом приводит к формуле:
| (1 – t2)(1 – t4)(1 – t6) ... (1 – t)(1 – t3)(1 – t5) ... | = 1 + t + t3 + t6 + t10 + ... |
Эти две формулы получены Гауссом. Нечего и говорить, что это удивительно красивые формулы!
Тождества Роджерса–РамануджанаВ заключение я хочу познакомить вас с двумя знаменитыми тождествами теории разбиений, для которых до сих пор не найдено прозрачных доказательств, хотя эта задача и по сей день остаётся в сфере интересов многих математиков.
Первое тождество. Число разбиений натурального числа п, в которых разность между любыми двумя частями превосходит единицу, равно числу разбиений числа п на части, дающие при делении на 5 остаток 1 или 4.
Второе тождество. Число разбиений натурального числа п, в которых разность между любыми двумя частями и каждая часть превосходят единицу, равно числу разбиений числа п на части, дающие при делении на 5 остаток 2 или 3.
Конечно, закономерность, утверждаемая этими тождествами, в высшей степени красива и нетривиальна, и неудивительно, что крупнейший английский математик начала XX века Г. Харди, узнавший о них из письма Рамануджана, датированного 16 января 1913 года, пришёл в восхищение. *)
При чтении этой статьи у вас, может быть, сложилось впечатление, будто теория разбиений напоминает кунсткамеру, в которую заботливо собраны различные экзотические экспонаты, никак или почти никак между собой не связанные. До недавнего времени так оно и было. Ситуация коренным образом изменилась лишь в 70-х годах XX века, когда английскому математику Яну Макдональду удалось найти единый подход к доказательству большого класса тождеств теории разбиений и открыть много новых, объединив их в стройную теорию (тождество Гаусса–Якоби включается в неё). **) Для тождеств Роджерса–Рамануджана и многих аналогичных тождеств общего подхода не найдено, хотя в последнее время и появились алгебраические методы их доказательств. Так что, понимание истинной природы этих тождеств, вероятно, ещё впер
Похожие работы
... и k+1<m+n+2 m+n<k и m+n>k-1 Такого для натуральных чисел тоже не может быть. Получаем противоречие, следовательно, теорема доказана. В следующем параграфе рассмотрены упражнения о разбиениях натурального ряда, при решении которых используются результаты данного параграфа. §3. Упражнения Упражнение 1 Пусть последовательность задана формулой .Найти . 1 … 28 29 30 31 ...
... , края отрезков сливаются в точку, оставаясь при этом рациональными числами. Логический вывод гласит, что исходный отрезок оказывается заполненным одними лишь рациональными числами, иными словами ни для какой "иррациональности" места не остается. Другое доказательство наоборот приводит к тому, что некоторые точки на прямой не могут быть заданы ни целыми, ни дробными числами, т.е. не являются ...
... осознать ключевые преимущества мультимедиа и стремиться максимально использовать именно их. Глава 2. Практическое применение мультимедиа на уроках математики 2.1. Конспект урока по математике в 6 «а» классе школы №16 (приложение 2) Тема: Деление положительных и отрицательных чисел Цели: (слайд 1) 1. научить делить положительные и отрицательные числа 2. закрепить ...
... не равных одновременно нулю; здесь D = 3/4. Конечно, случай положительно определённых бинарных квадратичных форм крайне прост, и результат задачи был известен задолго до возникновения геометрии чисел. Однако на положительно определённых бинарных квадратичных формах относительно просто проводятся некоторые рассуждения геометрии чисел, так что эти формы удобно использовать в качестве иллюстрации ...


0 комментариев