Навигация
Логарифмом числа b наз-ся показатель степени в к-рую нужно возвести основание а чтобы получить число b
2. Логарифмом числа b наз-ся показатель степени в к-рую нужно возвести основание а чтобы получить число b.
Из опр-ия имеем: a^ logab =b (осн-ое лог-ое тождесто)
Св-ва логарифмов: При любом а>0(а¹1), и любых пол-ных х и у выполняются следующие св-ва:
loga1=0
logaа=1
loga(ху)= logaХ+ logaУ
Док-во: Воспользуемся осн-ным лог-им тождеством
a ^ logab =b и св-ом показат-ной ф-ции
а^ х+у =а^x * а^y имеем
а^ loga(xy)=xy= a^ logax *a^ logay =a ^logax +logay
loga(Х/У)= logaХ- logaУ
logaХ^Р= рlogaХ
Формула перехода:
logaХ= logbX/ logbA
Билет №10.
1. Ф-ция F наз-ся первообразной ф-ции f на промежутке I, если для всех значений аргумента из этого промежутка F¢(x)=f(x). Например ф-ция F(x)=4x^2+3x-1 явл-ся первообразной ф-ции f(x)=12x^3 на множестве всех действительных чисел. Действительно F¢(x)=12X^2+3 , т.е. F¢(x)=f(x).
2. Если каждому действительному числу поставлен в соответствие его тангенс , то говорят , что задана ф-ция тангенс. Обозначается это так: y=tg x.
Св-ва:1) Областью опр-ния ф-ции явл-ся все действительные числа, кроме чисел вида
X=пи/2 +пи k, kÎZ.
Это следует из опред-ия тангенса (tg x=sin x/cos x). Нужно искл-ть числа, при к-рых знаменатель cos x=0 т.е. х= пи/2+пи k, kÎZ.
2) Множеством значений ф-ции явл-ся все действительные числа:Е(у)=(-¥;+¥).
3) Ф-ция явл-ся нечетной ф-цией, т.е. для любого хÎD(y) выполняется нер-во tg(-x)=-tg x . покажем это, tg (-x)=sin (-x)/cos (-x)= -sin x/cos x= -tg x
4) Ф-ция явл-ся периодической с периодом пи k ,где k-целое кроме 0.Наименьшим положительным периодом тангенса явл-ся число пи.
5) Ф-ция тангенс принимает значения 0 при х=пи k, kÎZ. Решением ур-ия tg x=0 явл-ся числа х=пи k, kÎZ
6) Ф-ция tg принимает положительные значения при пи k<x<пи/2+ пи k, kÎZ.
Ф-ция tg принимает отрицательные значения при
-пи/2+пи k<x<пи k, kÎZ . Промежутки знакопостоянства следуют из опр-ия tg x=sin x/cos x.
7) Ф-ция tg возрастает на всей области опр-ия т.е. на промежутках (-пи/2+пи k; пи/2 +пи k) kÎZ
Билет №13
1) Для того чтобы найти наибольшее(наименьшее) значение ф-ции y=f(x) имеющее на отрезке [a;b] конечное число критических точек, нужно:1. Найти критические точки, принадлежащие отрезку[a;b] ; 2.найти значения ф-ции в критических точках принадлежащих отрезку [a;b] ;3. Найти значение ф-ции на концах отрезка;4. Из полученных чисел (значения ф-ции в критических точках и на концах промежутка ) выбрать наиболее наибольшее (наименьшее) .Пример: Найти наибольшее и наименьшее значение ф-ции y=x^3 –3x на отрезке [-1,5;3] . 1)D(y)=R; 2) найдем критические точки
y’ =3x^2 –3; А)y’ = 0 если 3x^2 -3=0; 3(x^2 –1)=0; x=0 или x=1. Б) точек в к-рых производная не существует нет. 3) y(-1)=-1+3=2; y(1)=1-3=2; y-(-1.5)=(1.5)^3-3* (-1.5)=(-1.5)^3+2*1.5^2=1.5^2(-1.5+2)=2.25*.5=1.125
y(3)=27-9=18; -2<1.125<2<18
y(1)<y(-1.5)<y(-1)<y(3).
Min [-1,5;3] y(x)=y(1)=-2
Max [-1,5;3] y(x)=y(3)=18
2) 1.sin a+ sin b = 2 sin (a+b)/2 *cos(a-b)/2,
2. sin a- sin b=2 sin(a-b)/2 *cos(a+b)/2,
3. cos a+ cos b=2 cos (a+b)/2*cos (a-b)/2
4. cos a- cos b=-2 sin (a+b)/2*sin (a-b)/2
1)Пусть a=x+y и b=x-y из этих равенств находим:
x=(a+b)/2 и y=(a-b)/2
2) выведем ф-лы для суммы и разности синусов.
Докажем формулу 1: Воспользовавшись формулами синуса суммы и синуса разности имеем sin a+sin b = =sin(x+y)+ sin(x-y)= sin x cos y+ sin y cos x+ sin x* cos y-sin y*cos x= 2sin x*cos y= 2 sin(a+b)/2*cos(a-b)/2. Таким образом sin a+ sin b=2sin(a+b)/2*cos(a-b)/2
Докажем формулу 2:
Sin a-sin b= sin (x+y)- sin(x-y)=sin x cos y+ sin y*cos x –sin x*cos y+sin y*cos x= 2 sin y*cos x=2 sin(a-b)/ 2 * cos(a+b)/2. Таким образом sin a- sin b=2 sin(a-b)/2 *cos(a+b)/2,
3) выведем ф-лы для суммы и разности косинусов.
Докажем формулу 4:
Cos a- cos b=cos(x+y)-cos(x-y)=cos x* cos y-sin x* sin y-cos x*cos y-sin x*sin y=-2sin x*sin y=-2sin(a+b)/2*sin(a-b)/2 Таким образом
cos a- cos b=-2 sin (a+b)/2*sin (a-b)/2
Билет №14
1) Пусть задана ф-ция y=f(x) ее график изображен на рис 49. Точка х1 является точкой максимума , х2 является точкой минимума, т.е. точки х1 и х2- точки экстремума. Значения ф-ции в точках экстремума наз-ся экстремумами ф-ции. Например, значения ф-ции y=cos x в точках x= 2 пи k,где k Î Z, явл-ся экстремумами (максимумами)ф-ции,т.е. Ymax=1
2) 1.Cos (a-b)=cos a*cos b +sin a*sin b;
2.cos (a+b)=cos a*cos b- sin a*sin b;
3. sin(a-b)=sin a*sin b- sin b*cos a
4. sin (a+b)=sin a*cos b+sin b*cos a
Докажем ф-лу (1): 1) проведем радиуо ОА, равный R, вокруг точки О на угол a и b (рис50). Получим радиус ОВ и радиус ОС. 2)Пусть В(х1;у1) С(х2;у2). 3) Введем векторы ОВ(х1;у1) , ОС(х2;у2)
4)По опр-ию скалярного произведения ОВ*ОС=х1*х2+у1*у2 (*) 5) по опр-ию синуса и косинуса х1=R*cos a, y1=R*sin a, x2=R* cos b, y2=R*sin b 6) заменяя в равенстве(*) х1,х2,у1,у2, получим ОВ*ОС=R^2*cos a*cos b+R^2*sin a*sin b (**). 7) По теореме о скалярном произведении векторов ОВ*ОС=|OB|*|OC|*cosÐ BOC=R^2 cosÐBOC,
ÐBOC= a-b(см. рис. 50) или ÐBOC= 2 пи-(a-b) (см. рис. 51) cos(2 пи-(a-b))=cos(a-b) следовательно ОВ*ОС=R^2*cos (a-b) (***) 8) Из неравенств (**) и (***) получим: R^2*cos(a-b)=R^2* cos a*cos b+R^2*sin a*sin b. Разделив левую и правую части на R^2¹0 получим формулу (1) косинуса разности Cos (a-b)=cos a*cos b +sin a*sin b;
С помощью этой формулы легко вывести формулу (2) косинуса суммы и (4) синуса суммы:
Cos (a+b)=cos(a-(-b))=cos a*cos(-b)+sin a*sin (-b)= cos a*cos b-sin a*sin b значит cos(a+b)=cos a*cos b- sin a*sin b. Докажем формулу (4): sin (a+b)=cos(пи/2-(a+b))=cos((пи/2-a)-b)=cos(пи/2-a)cos b+sin(пи/2-a)sin b=sin a*cos b+cos a*sin b Значит sin (a+b)=sin a*cos b+sin b*cos a
Докажем формулу (3) Применяя последнюю формулу имеем sin(a-b)=sin(a+(-b))=sin a*cos (-b)+sin(-b)*cos a=sin a*cos b-sin b*cos a. Значит sin(a-b)=sin a*cos b-sin b*cos a. При док-ве формул (1)-(4) были использованы следующие факты:1) формулы приведения 2)ф-ция y=sin x-нечетная, ф-ция y=cos x-четная. Из формул сложения пологая b=пи n/2, где n ÎN, можно вывести формулы привидения для преобразований выражений вида cos(пи*n/2 ±a), sin(пи*n/2 ±a). Например cos(пи*n/2 -a)= cos пи/2*cos a+sin пи/2*sin a=0+sin a=sin a. Аналогично выводятся следующие формулы:
Sin (пи-а)=sin a
Sin (пи+а)=-sin a
Sin (3 пи/2-а)=-cos a и т.п. Из формул сложения следуют формулы двойного аргумента:
Sin 2a=2sin a*cos a
Cos 2a=cos^2 a-sin^2 a
Билет №11
1)Пусть на отрезке [a;b] задана непрерывная и неотрицательная функция y=f(x); S-площадь соответствующей криволинейной трапеции (рис42). Для вычисления площади S разобьём отрезок [a;b] на n равных отрезков, длинна каждого отрезка [Xj;Xj+1] равна b-a / n; на каждом из отрезков построим прямоугольник, высота которого равна значению функции f(Xj); площадь такого прямоугольника равна f(Xj)* DX=f(Xj) * b-a / n. При увеличении числа промежутков, на которые разбивается отрезок [a;b], ступенчатая фигура, состоящяя из прямоугольников, будет «мало отличатся» от криволинейной трапеции, и если Sn-сумма площадей всех прямоугольников, то Sn~=S. В курсе математического анализа показывается, что для любой непрерывной на отрезке [a;b] функции y=f(x) существует число, к которому стремится сумма площадей прямоугольников при неограниченном увеличении n(n ® ¥)). Это число называют интегралом, т.е. Sn ® integral (a;b) f(x) dx при n® ¥
2)Если каждому действительному числу поставлен в соответствие его синус, то говорят, что задана функция синус (обозначение y=sin x). Свойства функции синус 1) Область определения функции синус является множество всех действительных чисел, т.е. D(y)=R. Каждому действительному числу х соответствует единственная точка единичной окружности Px, получаемая поворотом точки P0(1;0) на угол, равный х радиан. Точка Рх имеет ординату, равную sinx. Следовательно, для любого х определено значение функции синус. 2) Множеством значений функции синус является промежуток [-1;1], т.е. E(y)=[-1;1]. Это следует из определения синуса: ордината любой точки единичной окружности удовлетворяет условию –1 <= Ypx<=1, т.е. –1<=sin x<=1 3)Функция синус является нечётной, т.е. для любого х принадлежащего R выполняется равенство sin(-x)=-sinx. Пусть точка Рх получена при повороте точки Р0 на х радиан, а точка Р-х получена при повороте точки Р0 на –х радиан (рис 43). Треугольник ОрхР-х является равнобедренным; ON-биссектриса угла РхОР-х, значит, ON является медианой и высотой, проведённой к стороне РхР-х. Следовательно, PxN = P-xN, т.е. ординаты точек Рх и Р-х одинаковы по модулю и противоположны по знаку. Это означает, что sin(-x)=-sinx. 4) Функция синус является периодической с периодом 2ПиR, где R- целое. Кроме 0. Наименьшим положительным периодом синуса является число 2Пи. Каждому действительному числу вида x+2ПиR, где R принадлежит Z, соответствует единственная точка единичной окружности Рх + 2ПиR, получаемая поворотом точки Р0(1;0) на угол x+2ПиR имеет ординату, равную sinx или sin(x+2ПиR). Таким образом, sin(x+2ПиR)=sinx. Этим показано, что числа вида 2ПиR, где R- целое, кроме 0, являются периодом функции. При R=1 имеем sin(x+2Пи)=sinx, следовательно, число 2Пи также является периодом функции синус. Покажем, что 2Пи-наименьшее положительное число, являющееся периодом функции синус. Пусть Т – положительный период функции синус; тогда sin(x+T)=sinx при любом х. Это равенство верно и при x= Пи.2, т.е. sin(пи/2 + T)=sin Пи/2 = 1. Но sinx=1,если x= Пи/2 + 2Пиn, где n принадлежит Z. Наименьшее положительное число вида 2Пиn есть 2Пи. 5) Функция синус принимает значение нуль при x=ПиR, где R принадлежит Z. Решением уравнения sinx=0 являются числа x=ПиR, где R принадлежит Z. 6) Функция синус принимает положительные значения при 2ПиR<x<Пи+2ПиR, где R принадлежит Z. Функция синус принимает отрицательные значения при Пи+2ПиR<x<2Пи+2ПиR, где R принадлежит Z. Промежутки знакопостоянства (рис44) следует из определения синуса. 7) Функция синус возрастает на промежутках [-Пи/2 + 2ПиR; Пи/2 + 2ПиR], где R принадлежит Z, и убывает на промежутках [Пи/2 + 2ПиR; 3Пи/2 + ПиR], где R принадлежит Z Докажем, что функция синус возрастает на промежутке [-Пи/2; Пи/2]. Пусть х1принадлежит [-Пи /2; Пи /2] и х2>x1. Сравним два значения функции: sinx2 – sinx1 = 2cos x1+x2/2 * sin x2-x1/2; 0< x2-x1/2 <= Пи/2, -Пи/2 < x1+x2/2< Пи/2, поэтому, учитывая промежутки знакопостоянства синуса и косинуса, имеем sin x2-x1/2 > 0, cos x1+x2/2>0. Таким образом, sinx2-sinx1>0, значит, большему значению аргумента соответствует большее значение функции, т.е. функция синус возрастает на промежутке [-Пи/2; Пи/2]. В силу периодичности синуса можно утверждать, что синус возрастает на промежутках [-Пи/2 + 2ПиR; Пи/2 + 2ПиR], где R принадлежит Z. 8) Функция синус имеет максимумы , равные 1, в точках Пи/2 + 2ПиR, где где R принадлежит Z. Функция Синус имеет минимумы, равные –1, в точках 3Пи/2 + 2ПиR, где R принадлежит Z. Покажем, что точка х0=Пи/2 является точкой максимума. Функция синус возрастает на промежутке [-Пи/2; Пи/2], т.е. sinx<sinПи/2 для любого х принадлежащего [-Пи/2 ; пи/2]. Функция синус убывает на промежутке [Пи/2; 3Пи/2], т.е. sin x < sin Пи/2 для любого х принадлежащего [Пи/2; 3Пи/2]. Ледовательно, х0+Пи/2 является точкой максимума (по определению), а значение sinx=1 является максимумом. В силу периодичности функции синус можно утверждать, что в точках Пи/2 + 2ПиR, где R принадлежит Z, функция имеет максимум, равный 1. 9) Функции арксинус дифференцируема в каждой точке области определения; производная вычисляется по формуле (sin x)’=cosx. (рис 45)
Билет №12
1)Пусть функция y=f(x) непрерывна на отрезке [a;b]; F-первообразная функции. В этом случае интеграл (a;b) f(x)dx = F(b) – F(a). Пример Вычислить : Интеграл (0;Пи)cos(2x – Пи/4) dx = ½sin(2x – Пи/4)|(0;Пи)= ½sin(2Пи - Пи/4) – ½sin(-Пи/4)=½sin(-Пи/4) + ½sin(Пи/4)=-SQR2/4 + SQR2/4 = 0.
2)Если каждому действительному числу поставить в соответствие его косинус, то говорят, что задана функция косинус. Свойства функции косинус 1)D(y)=R Каждому действительному числу х соответствует единственная точка единичной окружности Рх, получаемая поворотом точки Р0 (1;0) на угол х радиан. Точка Рх имеет абсциссу, равную cos x. Следовательно, для любого х определено значение функции y=cosx. 2)Множеством значений функции косинус является промежуток [-1;1], т.е. E(y)=[-1;1]. Это следует из определения косинуса: абцисса любой точки единичной окружности удовлетворяет условию –1<=Xpx <=1, т.е. –1<= cosx<=1. 3)Функция косинус является чётной, т.е. для любого x Î R выполняется равенство cos(-x)=cosx. Пусть точка Рх получина при повороте точки Ро на х радиан, а точка Р-хполучина при повороте точки Р0 на –х радиан(рис46). Треугольник ОрхР-х является равнобедренным; ON – биссектриса угла РхР-х, значит, является и высокой, проведённой к стороне РхР-х. Из этого следует, что точки Рх и Р-х имеют одну и ту же абсциссу ON, т.е. cos(-x)=cosx. 4)Функция косинус является периодической с периодом 2ПиR, где R-целое, кроме 0. Наименьшим положительным периодом косинуса являеися число 2Пи. Каждому действительному числу вида x+2ПиR, где RÎZ,соответствует единственная точка единичной окружности Рх+2ПиR, получаемая поворотом точки Р0 (1;0) на угол (x+2ПиR) радиан. Точка Рх+2ПиR имеет абсциссу, равную cosx или cos(x+2ПиR), где RÎZ. Таким образом, cosx=cos(x+2ПиR). При R=1 имеем cosx=cos(x+2Пи), следовательно, число 2Пи является периодом функции косинус. Покажем, что 2Пи – наименьший положительный период. Пусть Т-положительный период косинуса; тогда cos(x+T) = cosx при любом значении х. Это равенство должно быть верно и при х=0, т.е. cosT = cos0=0, следовательно, cosT=0. Но cosT=0, если T=2ПиR, где RÎZ. Наименьшее положительное число вида 2ПиR есть 2Пи. 5)Функция косинус принимает значение нуль при х=Пи/2 + ПиR, где RÎZ. Решением уравнения cosx=0 являются числа х+Пи/2+ПиR, где RÎZ. 6)Функция косинус принимает положительные значения при –Пи/2 + 2ПиR<x<Пи/2 + 2ПиR, где RÎZ. Функция косинус принимает отрицательные значения при Пи/2 + 2ПиR<x<3Пи/2 + 2ПиR, где RÎZ. Промежутки знакопостоянства (рис47) следуют из определения косинуса. 7)Функция косинус возрастает на промежутках [-Пи + 2ПиR; 2ПиR], где RÎZ, и убывает на промежутках [2ПиR; Пи+2ПиR], где RÎZ. Чтобы доказать утверждение о промежутках возрастания функции косинус, заметим, что cosx=sin(Пи/2+х). Функция y+sin(Пи/2 + х) возрастает, если –Пи/2 + 2ПиR<=Пи/2 + x<=Пи/2 + 2ПиR, где RÎZ; т.е. если –Пи + 2ПиR, где RÎZ; т.е. если –Пи+2ПиR<=x<=2ПиR, где RÎZ. Поскольку sin(Пи/2 + х)=cosx, функция y=cosx возрастает, если –Пи+2ПиRR<=x<=2ПиR, где RÎZ. Аналогично обосновывается утверждение о промежутках убывания функции. 8)Функция косинус имеет максимумы, равные 1, в точках 2ПиR, где RÎZ. Функция косинус имеет минимумы, равные –1, в точках Пи+2ПиR, где RÎZ. Покажем, что функция y=cosx имеет максимумы в точках 2ПиR, где RÎZ. Замечая, что cosx=sin(Пи/2 + х), найдём точки максимума функции y=sin(Пи/2+x). Её точки максимума Пи/2 + х=Пи/2+2ПиR, где RÎZ, т.е. x=2ПиR, где RÎZ. Максимум функции косинус равен 1. Аналогично проводятся рассуждения о точках минимума. 9)Функция косинус непрерывна на всей области определения.10) Функция косинус дифференцируема в каждой точке области определения; производная функции косинус вычисляется по формуле (cosx)’=-sinx.
Билет №15
1.Если производная функции равна 0 на некотором промежутке, то эта функция постоянна на этом промежутке.
Если g¢(x)=0 на некотором промежутке то касательная к графику функции y=g(x), например g(x)=6 в каждой точке данного промежутка параллельна оси ОХ.
2.Если f- непрерывная и неотрицательная функция на отрезке[а;b], то площадь соответствующей криволинейной трапеции можно выч-ть по формуле
S=F(b)-F(a)
Док-во:
Пусть y=S(x) –площадь криволинейной трапеции, имеющей основание [a;x] где xÎ[а;b], заметим что S(a)= 0 S(b)=S
Покажем что y=S(x)-первообразная ф-ция y=f(x)
т.е. S¢(x)=f(x) что бы найти производную ф-ции y=S(x),
воспользуемся опр-ем производной:
а) зададим преращение ∆x (пусть ∆x >0)
б) найдем приращение ф-ции
∆S=S(x+∆x)-S(x)
в) составим соотношение
∆S/∆x=S(x+∆x)-S(x)/ ∆x
г) выясним чему равен предел отношения при ∆x®0Разность S(x+∆x)-S(x) равна площади криволинейной трапеции с основанием [x; x+∆x]
Если ∆x®0 то эта площадь приблизительно равна площади прямоугольника f(x)* ∆x т.е.
S(x+∆x)-S(x) »f(x) * ∆x
Имеем
S(x+∆x)-S(x)/ ∆x »f(x)
При ∆x®0. Этим показано что S¢(x)=f(x)
3)Равенство S¢(x) =f(x) означает что S- первообразная функцииf на заданном промежутке.
3)По основному св-ву первообразной имеем F(x)=S(x)+C, где F- какая-либо первообразная для f.
При x=a получим ,что
F(a)=S(a)+C т.е. C=F(a).
При x=b имеем
F(b)=S(b)+F(a)
Следовательно
S=S(b)=F(b)-F(a)
Билет №16
1)Пусть задана функция y=f(x), дифференцируемая в каждой точке промежутка I, точки a и b принадлежат этому промежутку. На интервале (a;b) найдётся такая точка с, для которой выполняется равенство f’(x)= f(b)-f(a)/b-a. Геометрически этот факт можно истолковать следующим образом. Пусть функция y=f(x) дифференцируема на некотором промежутке. Точки a и b принадлежат этому промежутку; через точки A(a;f(a)) и B(b;f(b)) проведена секущая. Тогда на интервале (a;b) найдётся такая точка с, что угловой коэффициент касательной, проведённой через точку (с; f(c)), будет равен угловому коэффициенту секущей АВ (рис 55).
2)Функция заданная формулой f(x)=x^a, называется степенной. Свойства степенной функции при а>1 1)D(f)=[0;+¥], если а не является натуральным числом. Это следует из определения степени с рациональным показателем. Если а натуральное число, то D(f)=(-¥;+¥) по определению степени с натуральным показателем. 2)E(f)=[0;+¥) для всех а>1, кроме а= 2R+1. Где RÎN. Это следует из определения степени с рациональным показателем. E(f)=(-¥;+¥) для нечётных а,т.е. а=2R+1, где RÎN. 3)Если а-чётное натуральное число, то данная функция является чётной. Т.к. f(-x)=(-x)^2R = ((-x)^2)^R= (x^2)^R = x^2R = f(x). Если а-нечётное натуральное число. то данная функция является нечётной, так как f(-x)=(-x)^2R+1 + (-x)^2R (-x)= x^2R * (-x)=-x^2R * x+ -x^2R+1 + -f(x). 4)При х=0 функция f(x)=0, так как 0^a = 0 при а>0. 5)При x>0 функция f(x)>0. Это следует из определения степени с рациональным показателем. При нечётных а(а=2R+1, RÎN), если х<0, функция принимает отрицательные значения. Так как x^2R+1+x^2R, x^2R>0, но x<0, следовательно, произведение x^2R x<0, т.е. f(x)<0 при x<0. 6) Функция является возрастающей на промежутке [0;+¥) для любого a>1. Из свойства степени с рациональным показателем (r-рациональное число и 0<a<b, тогда a^r<b^r при r>0) следует, что x1^a<x2^a. Таким образом, меньшему значению аргумента соответствует меньшее значение функции, т.е. функция y=f(x) возрастает на промежутке [0;¥). Докажем, что если ф- нечётное число, то функция возрастает и на промежутке (-¥;0] (рис56б). Пусть x1<x2<0, тогда x1^a< x2^a по определению степени с целым отрицательным показателем. Т.е. данная функция возрастает по определению возрастающей на промежутке функции. Аналогично можно доказать, что функция y=f(x) на промежутке (-¥;0] убывает, если а – чётное целое (рис56а).
Билет №17
Пусть задана сложная ф-ция g(x)=f(kx+b).
Если ф-ция f имеет производную в точке kx0+b, то производную ф-ции g можно найти по формуле g¢(x0)=kf¢(kx0+b).
Например найдем производную ф-ции g(x)=(7x-9)^19
g¢(x)=7*19(7x-9)^18=133(7x-9)^18
Похожие работы
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
... данным, n=20 Найти матрицу А-1, обратную к матрице А и с ее помощью решить систему А =, где , = , = . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИКА (углубленный курс) Билет № 12 Что называется характеристическим уравнением дифференциального уравнения II порядка с постоянными коэффициентами? По какой ...
... быть выведены на печать. На экране рисунки могут быть статическими (неподвижными) или динамическими (движущимися). В последнее время машинная графика выделилась в самостоятельный раздел информатики с многочисленными приложениями. Средствами машинной графики создается не только печатная продукция, но и рекламные ролики на телевидении, мультфильмы. Объясним, как кодируется изображение в памяти ...
... уроки сказки, веселые задачи в стихах, математические загадки, сказочные задачи, математические сказки, задачи занимательного характера, головоломки, кроссворды и логические задачи способствуют активизации мыслительной деятельности учащихся на уроках математики, подтвердилась. Для себя лично я усвоила правило: "Не бери игру на урок, для того чтобы развлечься. Все на уроке должно быть логически ...




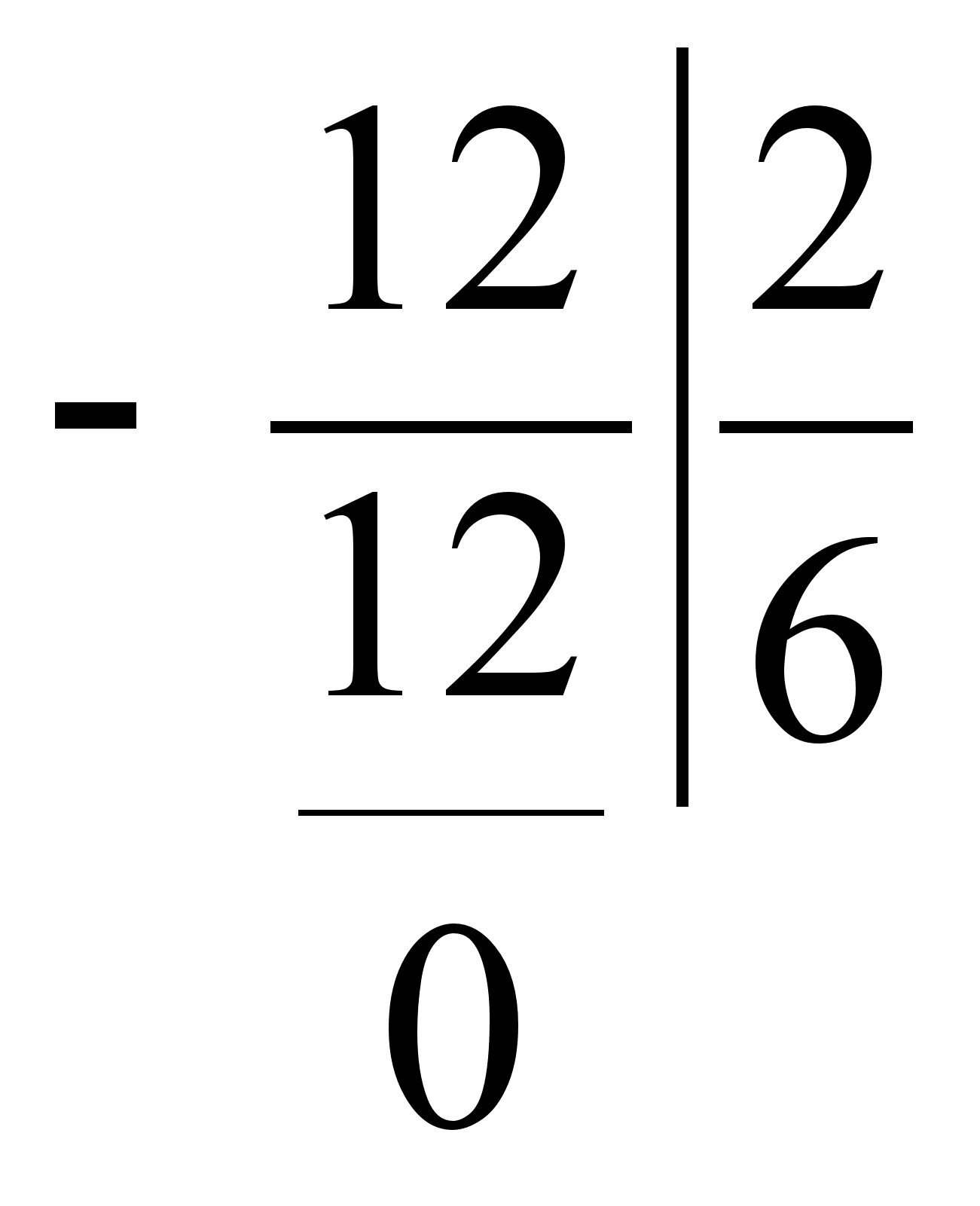

0 комментариев