Навигация
Проверка гипотезы о равенстве генеральных средних при известных дисперсиях. Признак x и h распределены нормально с известными дисперсиями
37. Проверка гипотезы о равенстве генеральных средних при известных дисперсиях. Признак x и h распределены нормально с известными дисперсиями.
Пусть по выборкам x1, x2, ... , xn объема n, h1, h2, ... , hm объема m, получены выборочные средние значения (![]() ;
; ![]() ). Выдвигается гипотеза о равенстве генеральных средних: H0: M(x) = M(h); При конкурирующей гипотезе:
). Выдвигается гипотеза о равенстве генеральных средних: H0: M(x) = M(h); При конкурирующей гипотезе:
![]() - СВ:
- СВ:
Д(Z)- дисперсия Д((![]() -
- ![]() )/s(
)/s(![]() -
-![]() )) =
)) = ![]()
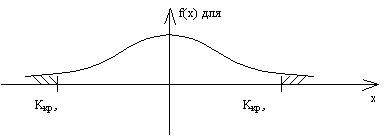
M(Z) = 0; Д(Z) = 1. Для того, чтобы выбрать Zкр. и при заданном уровне значимости a, определить принимается или не принимается основная гипотеза, найти вероятности.
P(0 < Z < Zкр.) + P(Z > Zкр. прав.) = ½ Ф(Zкр.) + a/2 = ½ Ф(Zкр. прав.) = ½ - a/2
Zнабл. = 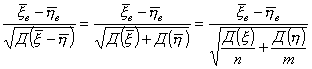
|Zнабл.| < Zкр.прав. Þ Н0 |Zнабл.| > Zкр.прав. Þ Н0 отвергается.
38. Проверка гипотезы о равенстве генеральных средних при неизвестных дисперсиях.
Пусть x и h нормально распределенные СВ, предполагается, что неизвестны, но равны между собой дисперсии. x1, x2, ... , xn h1, h2, ... , hm
![]() ;
; ![]() : Н0: М(x) = М(h) Н1: М(x) ¹ М(h)
: Н0: М(x) = М(h) Н1: М(x) ¹ М(h)
Для проверки гипотезы Н0, вводится СВ t, которая представляет собой
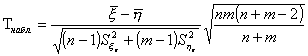
Теоретическое обозначение признака; СВ Т распределена по закону Стъюдента, зависит от первого параметра, который называется числом степеней свободы (k).
k = n + m – 2 (по таблице для распределения Стъюдента при заданном значении k и уровне значимости a в зависимости от вида альтернативной и конкурирующей гипотезы, находятся либо односторонние tкр., либо двухсторонние tкр.).
Ткр. прав. = - Ткр. лев. | Тнабл. | < Ткр. двуст. Þ Н0 | Тнабл. | > Ткр. двуст. Þ Н0 отвергается.
42. Марковские случайные процессы. Размеченный граф состояний.
Предположим, что дана система S. Предп., что состояние этой сис-мы хар-ся параметрами состояний. Если состояние системы меняется во времени случайно, то говорят, что в сис-ме протекает случайный процесс. Сис-ма —аудитория. Для хар-ки состояния используется параметр—число студентов, тогда эта система с дискретными состояниями. Будем рассматривать системы с дискретными состояниями и непрерывным t: сис-ма мгновенно в произвольные сегменты t скачками меняет состояние. Если параметр t принимает дискретные значения (t=1,2,3,...), то происходит процесс с дискретным временем (случайная последовательность), если же t изменяется на некотором интервале, то процесс с непрерывным временем. Если случайные величины семейства принимают дискретные значения, то имеет место процесс с дискретными значениями, если же непрерывное, то с непрерывными значениями. Предположим, что рассматривается система с дискретными состояниями и непрерывным t. Пусть S1, S2,...,Sn —возможные состояния сис-мы. Для описания процесса, происх. в сис-ме, надо знать вер-ти каждого состояния на произвольный момент t. Р1(t)—вер-ть того, что в момент t сис-ма находится в 1-ом состоянии. Процесс, протекающий в системе, наз. марковским, если для него вероятность попасть в состояние Xi=Si в момент ti зависит не от всего прошлого, а лишь от состояния Xi-1=Si, в котором процесс был в предыдущий момент времени ti-1. Графом называется совокупность вершин и дуг, соединяющих эти вершины. Для описания процесса, протекающего в системе, удобно использовать размеченный граф состояний, в котором в кач-ве вершин исп-ся различные состояния системы, а в кач-ве дуг—стрелки, показ. возможные переходы за 1 шаг из состояния в состояние. При этом над каждой стрелкой указ. Плотность вероятности соответствующего перехода.
Похожие работы
... вокруг своей оси и вокруг Солнца Земля - лишь ничтожная пылинка в беспредельном мироздании. Идеи Николая Кузанского и Джордано Бруно зало-жили основы для развития философии и естествознания Нового времени. 17.Формування філософського мислення нового часу. Ф.Бекон і його роль у розробці емпіризму та індуктивного методу пі ...
... и коммуникационных технологий при обучении школьников, в том числе, при обучении математике?». Поэтому методическая проблема, над которой я работаю последнее время, это – «Использование информационно-коммуникационных технологий на уроках математики, как средство повышения мотивации учения». Задачей школы является не только сообщение определенной суммы знаний учащимся, но и развитие у них ...
... и это также под контролем, так как внеклассные интересы якобы отвлекали детей от занятий, и учащихся окружали всевозможные запреты. Таким образом, культурно-бытовой облик учащихся начальной и средней школы в XIX – начале XX века отличали две его специфические черты: возраст учащихся (они постоянно находились в стадии развития) и попытки непрерывного контроля над этим развитием самого учебного ...
... не различают (94,4%) разницы между «оценкой» и «отметкой». Анкетирование родителей (методика незаконченных предложений) Методика незаконченных предложений для родителей проводилась с целью выяснения влияния оценочной деятельности учителя на взаимоотношения ученика и его семьи. Было опрошено 9 родителей, которым закончить 9 предложений. а) Фразы №№1 и 4 позволяют определить место школы в жизни ...
0 комментариев