Проверка гипотезы о равенстве генеральных средних при известных дисперсиях. Признак x и h распределены нормально с известными дисперсиями
Система дифф. уравнений Колмогорова для вероятностей состояний
Закон распределения числа событий за фиксированный промежуток времени и закон распределения интервала времени между событиями в простейшем потоке
Навигация
Закон распределения числа событий за фиксированный промежуток времени и закон распределения интервала времени между событиями в простейшем потоке
Математика (шпаргалка для экзамена)
44583
знака
0
таблиц
6
изображений
47. Закон распределения числа событий за фиксированный промежуток времени и закон распределения интервала времени между событиями в простейшем потоке.
Пусть рассматривается какой-то поток событий. С ним всегда можно связать дискретную СВ – число событий, происходящих за интервал длины t. Эта СВ дискретна. С этим же потоком можно связать НСВ – интервал времени между событиями. Т – интервал времени между событиями в потоке. Для простейшего потока доказано, что число событий, попадающих на интервал длины t является ДСВ, распределенной по закону Пуассона. Вероятность того, что за время t произойдет ровно k событий.
(a > 0)
a = t l, l - интенсивность простейшего потока
 |
при t = 1
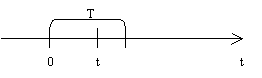Найдем закон распределения интервала времени между событиями простейшего потока. Выведем закон распределения интервала времени между событиями в потоке.
F(t) = ?
Fт(t) = P(T<t) = 1 – P(T ³ t) = 1 – Pt(k=0) = 1 - 
= 1 – e-lt, t ³ 0
Fт(t) = le-lt
Всякий простейший поток можно задать интенсивностью, либо задать среднее значение времени между событиями в потоке (Т).
Средняя продолжительность интервала времени 
; М(Т) = 
= 
Þ l = 
Многоканальная СМО с отказами.
СМО— система, предназначенная для обслуживания какого-то потока поступающих на вход в систему заявок. Система характеризуется наличием того или иного числа каналов обслуживания. Если в системе несколько каналов, то мы считаем эти каналы равноправными, и они имеют одинаковые хар-ки (среднее число заявок, обслуж. 1-им каналом при непрерывной работе за единицу времени—одно и то же для всех каналов). Пусть СМО имеет n каналов обслуживания и на вход в систему поступает простейший поток заявок с интенсивностью l. Будем считать, что среднее время обслуживания одной заявки одним каналом Тоб=1/m; продолж. Обслуж. Тоб—СВ, распределенная по показательному закону с параметром m. Тогда при непрерывной работе канала он может обслужить m заявок в единицу времени (технич., профес. Хар-ка каналов).
Пусть в случае, когда заявка, поступившая в систему, застает свободный хотя бы один канал, то она поступает сразу под обслуживание каким-то одним каналом. Если же заявка поступает в момент занятости всех каналов, то она получает отказ в обслуживании и покидает систему необслуженной. Нарисуем граф состояний таких СМО, при этом нумерацию состояний будем вести по числу заявок, находящихся в системе: S0—заявок нет S1—одна заявка, один канал занят, n-1 каналов свободно ,,, Sn—n заявок, n каналов занято, нет свободных.
l l l l
S0
S1
S2
Sn-1
Sn
2m 3m (n-1)m nm
Вероятности состояний:
Р0=(1+
)-1
P1=
; P2=(l2/(2!m2))*P0;....;Рr=(lk/k!mk)*P0
Ротказа=Рn ( все каналы заняты).
Относительная пропускная способность системы (вер-ть обслуживания) q=1—Pотказа=1—Рn
Абсолютная пропускная способность(ср. число заявок, обслуж. за единицу времени) A=lq
Среднее число занятых каналов 
=Aq/m
Можно найти двумя способами:
кзан—число занятых каанлов—СВ . 
зан=М(кзан)=
зан=A/m
5. 
незан=n—
зан 7. Степень загруженности каналов s=
зан/n
Многоканальная СМО с ограниченным числом мест в очереди.
СМО— система, предназначенная для обслуживания какого-то потока поступающих на вход в систему заявок. Система характеризуется наличием того или иного числа каналов обслуживания. Если в системе несколько каналов, то мы считаем эти каналы равноправными, и они имеют одинаковые хар-ки (среднее число заявок, обслуж. 1-им каналом при непрерывной работе за единицу времени—одно и то же для всех каналов). Пусть дана сис-ма с простейшим потоком, инт-ть которого l, один канал в среднем может обслужить m заявок в единицу времени. Пусть в сис-ме имеется m мест для постановки заявок в очередь. Предположим, что заявка, заставшая в момент своего поступления один канал свободным, тут же обслуж. Если же в момент поступления заявки все каналы заняты, но имеется хотя бы одно свободное место в очереди, то заявка становится в очередь на обслуживание, при этом как только один из каналов освобождается, одна заявка из очереди поступает на обслуживание. Если заявка, поступившая в систему, застает занятыми все каналы и места в очереди, то она получает отказ в обслуживании и покидает систему. Возможные состояния системы: S0—заявок нет S1—одна заявка, n-1 канал свободен, все места в очереди свободны Sn—n заявок, все каналы заняты, все места в очереди свободны Sn+1—все каналы заняты, 1 заявка в очереди, m-1 мест в очереди свободны Sn+m—все каналы заняты, m мест (все) в очереди заняты.
l l l l l
S0
S1
S2
Sn-1
Sn
Sn+1
Sn+m
 |  |  |  |  |
2m 3m nm nm nm
Предельные вероятности состояний:
Р0=(1+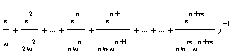
1.Ротказа=Рn+m=
=
2.Относительная пропускная сп-ть q=1—Pn+m 3.Абсолютная пропускная сп-ть A=lq 4.Среднее число заявок в очереди
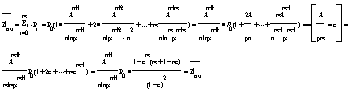
5. 
. 6.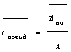 
Многоканальная СМО с неограниченным числом мест в очереди.
Многоканальная СМО с отказами.
СМО— система, предназначенная для обслуживания какого-то потока поступающих на вход в систему заявок. Система характеризуется наличием того или иного числа каналов обслуживания.
Если в системе несколько каналов, то мы считаем эти каналы равноправными, и они имеют одинаковые хар-ки (среднее число заявок, обслуж. 1-им каналом при непрерывной работе за единицу времени—одно и то же для всех каналов).
Пусть число мест в очереди не ограничено. Хар-ки этой СМО получим из характеристик СМО с ограниченным количеством мест в очереди, предполагая, что m—>¥. Тогда в выражении для Р0 имеем
Р0=
=
При m —>¥ å1+e+e2+...+em-1 сходится только в том случае, если 0<e<1; если e>=1 сумма расходится, т.е. для этой СМО процесс не является транзитивным. Следовательно, предельные вер-ти состояний не существенны.
Будем считать, что при m—>¥, e<1 . Следовательно предельн. вер-ти сост-й сущ. и хар-ки СМО след.:
Ротказа=0
q=1 каждая заявка будет обслужена
.
Среднее время ожидания 
. 6.A=lq=l. 7.
Похожие работы
... вокруг своей оси и вокруг Солнца Земля - лишь ничтожная пылинка в беспредельном мироздании. Идеи Николая Кузанского и Джордано Бруно зало-жили основы для развития философии и естествознания Нового времени. 17.Формування філософського мислення нового часу. Ф.Бекон і його роль у розробці емпіризму та індуктивного методу пі ...
... и коммуникационных технологий при обучении школьников, в том числе, при обучении математике?». Поэтому методическая проблема, над которой я работаю последнее время, это – «Использование информационно-коммуникационных технологий на уроках математики, как средство повышения мотивации учения». Задачей школы является не только сообщение определенной суммы знаний учащимся, но и развитие у них ...
... и это также под контролем, так как внеклассные интересы якобы отвлекали детей от занятий, и учащихся окружали всевозможные запреты. Таким образом, культурно-бытовой облик учащихся начальной и средней школы в XIX – начале XX века отличали две его специфические черты: возраст учащихся (они постоянно находились в стадии развития) и попытки непрерывного контроля над этим развитием самого учебного ...
... не различают (94,4%) разницы между «оценкой» и «отметкой». Анкетирование родителей (методика незаконченных предложений) Методика незаконченных предложений для родителей проводилась с целью выяснения влияния оценочной деятельности учителя на взаимоотношения ученика и его семьи. Было опрошено 9 родителей, которым закончить 9 предложений. а) Фразы №№1 и 4 позволяют определить место школы в жизни ...
0 комментариев