Навигация
Система дифф. уравнений Колмогорова для вероятностей состояний
43. Система дифф. уравнений Колмогорова для вероятностей состояний.
Пусть дан марковский случайный процесс. Рi(t)—вер-ти состояний: i=1,n(все с чертой), тогда для Рi(t) выполняется следующее дифференциальное уравнение
d Рi(t)/dt=å( от i<>k,k=1 до n) lki* Рi(t)—å( от j<>1,j=i до n) lij*Pi(t); i=1,n(все с чертой) (1) Система из n уравнений , т.к. для любого момента t å( от i=1 до n) Pi(t), то в системе (1) одно любое уравнение м-но отбросить. И, задав начальное условие на момент t=t0, P1(t0)=1, Pi(t0)=0, i=1,n( все с чертой).
В итоге м-но решить сис-му дифф. ур-ний и найти все вер-ти состояний Pi(t), i=1,n(все с чертой).
44. Предельные вероятности состояний. Нахождение предельных вероятностей.
Предположим, что дан марковский случайный процесс, тогда, используя уравнение Колмогорова, можно найти Рi(t); i = ![]()
Предельными или финальными вероятностями называют пределы
![]() , если эти вероятности существуют, т.е.
, если эти вероятности существуют, т.е. ![]() = Рi.
= Рi.
Если эти предельные вероятности существуют, то в системе устанавливается стационарный режим, при котором состояние системы меняется случайным образом, но вероятность каждого состояния остается неизменной.
Предельная вероятность в марковском случайном процессе существует, если этот процесс удовлетворяет свойству транзитивности. Процесс в протекающей системе называется транзитивным, если существует интервал времени t, в течение которого система может перейти из любого состояния Si в любое другое состояние Sj.
 Алгебраические уравнения для предельной вероятности состояний
Алгебраические уравнения для предельной вероятности состояний
Пусть марковский случайный процесс удовлетворяет свойству транзитивности, тогда для него при t ® ¥ существуют предельные вероятности состояний Pi=const.
![]()
![]() , Þ, в этом случае вместо дифференциального уравнения Колмогорова получили систему линейных уравнений относительно вероятности состояний
, Þ, в этом случае вместо дифференциального уравнения Колмогорова получили систему линейных уравнений относительно вероятности состояний
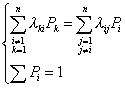
Одно уравнение отбрасывается, остается n уравнений, решая эту систему получаем Р1, Р2, ... , Рn.
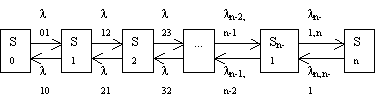 |
45. Процессы гибели и размножения. Формулы для нахождения предельных вероятностей.
![]() Мы предполагаем, что все потоки, переводящие систему из любого Si в Si+1 и из Si в Si-1 являются простейшими.
Мы предполагаем, что все потоки, переводящие систему из любого Si в Si+1 и из Si в Si-1 являются простейшими.
li, i+1
li, i-1
Процессы такого типа называются процессами гибели и размножения.
Составим систему уравнений для нахождения предельной вероятности состояний:
S0: l01P0 = l10P1 S1: l10P1 + l12P1 = l01P0 + l21P2 S2: l21P2 + l23P2 = l12P1 + l32P3 ... Sn: ln, n-1 Pn = ln-1, n Pn-1 P0 + P1 + P2 + ... + Pn = 1
![]() Из первого уравнения выражаем P1 =
Из первого уравнения выражаем P1 =
l01P0 + l12P1 = l01P0 + l21P2
P2 = ![]()
P3 = ![]() Pn =
Pn = ![]() ...
...
P0 + ![]()
![]() ... +
... + ![]() = 1
= 1
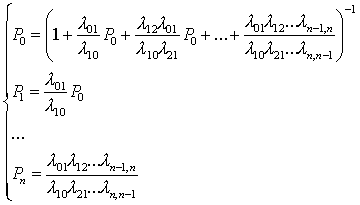
46. Потоки событий. Простейший поток и его свойства.
![]() Потоком событий называется последовательность каких-то однородных событий, следующих друг за другом через случайные интервалы времени, т.е. в произвольные моменты времени.
Потоком событий называется последовательность каких-то однородных событий, следующих друг за другом через случайные интервалы времени, т.е. в произвольные моменты времени.
Потоки избираются на числовой оси, представляющей ось времени, точками, соответствующими моменту наступления событий.
Например: - поток вызовов, поступающих на станцию скорой помощи;
- поток автомобилей, пересекающих перекресток.
Среднее число событий, происходящих в единицу времени называется интенсивностью потока. l - среднее число событий в потоке, происходящее за единицу времени. Свойства потока:
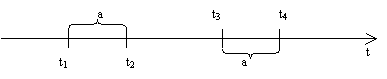
Поток называется стационарным, если вероятность наступления того или иного числа событий за интервал времени длины а зависит от длины этого интервала и не зависит от того, в какой момент времени начинается отсчет этого интервала.
t2 – t1 = a
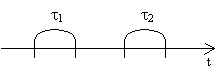 |
Поток событий называется потоком без последействия (без последствия), если для любых непересекающихся интервалов времени длины t1 и t2.
Вероятность появления того или иного числа событий в интервале t2 не зависит от того, какое число событий произошло в интервале t1.
Иначе, отсутствие последствия означает независимость наступления событий во времени.
3. Поток называется ординарным, если вероятность наступления двух и более событий за некоторый достаточно малый интервал времени ![]() t пренебрежимо мала по сравнению с вероятностью наступления одного события за этот интервал.
t пренебрежимо мала по сравнению с вероятностью наступления одного события за этот интервал.
Поток, обладающий всеми тремя перечисленными свойствами называется простейшим.
Похожие работы
... вокруг своей оси и вокруг Солнца Земля - лишь ничтожная пылинка в беспредельном мироздании. Идеи Николая Кузанского и Джордано Бруно зало-жили основы для развития философии и естествознания Нового времени. 17.Формування філософського мислення нового часу. Ф.Бекон і його роль у розробці емпіризму та індуктивного методу пі ...
... и коммуникационных технологий при обучении школьников, в том числе, при обучении математике?». Поэтому методическая проблема, над которой я работаю последнее время, это – «Использование информационно-коммуникационных технологий на уроках математики, как средство повышения мотивации учения». Задачей школы является не только сообщение определенной суммы знаний учащимся, но и развитие у них ...
... и это также под контролем, так как внеклассные интересы якобы отвлекали детей от занятий, и учащихся окружали всевозможные запреты. Таким образом, культурно-бытовой облик учащихся начальной и средней школы в XIX – начале XX века отличали две его специфические черты: возраст учащихся (они постоянно находились в стадии развития) и попытки непрерывного контроля над этим развитием самого учебного ...
... не различают (94,4%) разницы между «оценкой» и «отметкой». Анкетирование родителей (методика незаконченных предложений) Методика незаконченных предложений для родителей проводилась с целью выяснения влияния оценочной деятельности учителя на взаимоотношения ученика и его семьи. Было опрошено 9 родителей, которым закончить 9 предложений. а) Фразы №№1 и 4 позволяют определить место школы в жизни ...
0 комментариев