Министерство образования России
Специальные главы математики
Пояснительная записка
по теме: “ Теория вероятностей
и случайных процессов”
Студент: Ёлгин Д.Ю.
Куратор: Хоменко В.М.
НГТУ - 97
Случайныи образом выберем семейство кривых: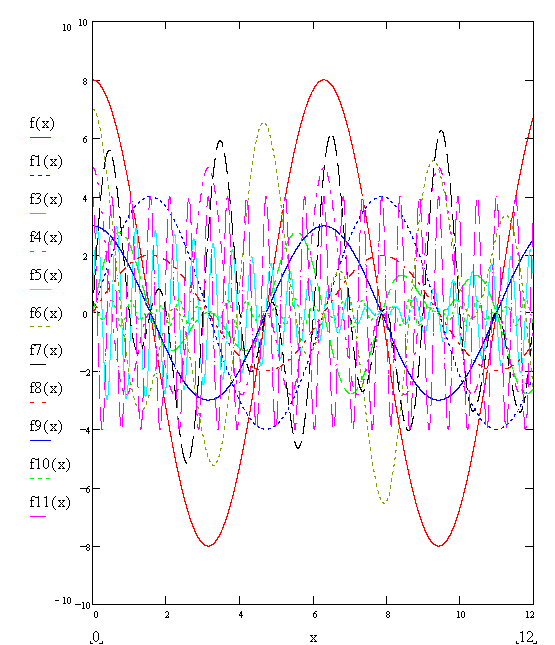
Примечание:
Наугад выбираются 14 кривых. Все кривые имеют синусоидальную форму. Область значений не привышает интервал [ -12; 12 ]. Для каждой функции вычисляем значения в точках 0, 2, 4, 6, 8, 10, 12 и составляем матрицу М1.
Составим матрицу рабочих значений М1:
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | |
| x1 | 8 | -3,329 | -5,229 | 7,681 | -1,164 | -6,713 | 6,751 |
| x2 | 0 | 3,637 | -3,027 | -1,118 | 3,957 | -2,176 | -2,146 |
| x3 | 0 | -1,227 | -1,235 | 1,594 | 0,565 | 0,777 | -2,609 |
| x4 | 5 | -1,998 | -2,758 | 3,17 | -0,309 | -0,647 | -0,54 |
| x5 | 0 | -2,502 | -1,606 | 0,276 | -0,086 | -0,725 | 1,086 |
| x6 | 7 | -0,324 | 1,008 | -1,245 | -6,437 | 0,99 | -2,705 |
| x7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| x8 | 0 | 1,819 | -1,514 | -0,559 | 1,979 | -1,088 | -1,073 |
| x9 | 3 | -1,248 | -1,961 | 2,881 | -0,437 | -2,517 | 2,532 |
| x10 | 0 | -0,161 | -0,317 | 0,26 | 0,026 | 0,372 | -0,394 |
| x11 | 4 | 1,697 | -2,561 | -3,869 | -0,722 | 3,257 | 3,485 |
| x12 | 0 | -2,377 | 0,44 | -0,943 | -3,79 | -0,888 | -0,91 |
| x13 | 2 | -0,832 | -1,307 | 1,92 | -0,291 | -1,678 | 1,688 |
| x14 | 0 | 0,909 | -0,757 | -0,279 | 0,989 | -0,544 | -0,537 |
4. Вычислим m[t]:
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| m[t] | 2,071429 | -0,424 | -1,48743 | 0,697786 | -0,40857 | -0,82714 | 0,330571 |
| Корелляционная матрица | |||||||
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | |
| 0 | 162,7092 | -36,6317 | -64,2259 | 64,14459 | -59,8507 | -46,1746 | 56,60024 |
| 2 | 50,93338 | 11,23673 | -48,7464 | 33,38392 | 25,55703 | -26,5632 | |
| 4 | 62,29164 | -45,8419 | -15,0293 | 43,78402 | -42,4137 | ||
| 6 | 102,2796 | -1,99387 | -72,1782 | 50,37741 | |||
| 8 | 78,75916 | -6,8851 | -3,53313 | ||||
| 10 | 73,80887 | -41,2532 | |||||
| 12 | 89,49557 | ||||||
Составим таблицу дисперсий и сигм:
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | |
| Дисперс | 162,7092 | 50,93338 | 62,29164 | 102,2796 | 78,75916 | 73,80887 | 89,49557 |
| Сигма | 12,75575 | 7,136762 | 7,892505 | 10,11334 | 8,874636 | 8,591209 | 9,46021 |
| Нормированная кор-матрица | |||||||
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | |
| 0 | 1 | -0,40239 | -0,63795 | 0,497232 | -0,5287 | -0,42135 | 0,469042 |
| 2 | 1 | 0,199491 | -0,67538 | 0,527091 | 0,416826 | -0,39344 | |
| 4 | 1 | -0,57432 | -0,21457 | 0,645723 | -0,56805 | ||
| 6 | 1 | -0,02222 | -0,83073 | 0,526551 | |||
| 8 | 1 | -0,0903 | -0,04208 | ||||
| 10 | 1 | -0,50758 | |||||
| 12 | 1 | ||||||
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| p[t] | 1 | -0,23289 | -0,48014 | 0,549149 | -0,22664 | -0,4074 | 0,469042 |
коэффициенты a1 и a1 графика y = a0 + a1x и выберем её в силу оптимальности:
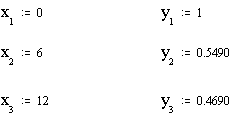
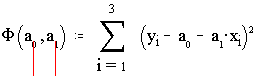
Составим систему уравнений:
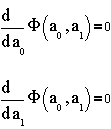
Из них вычислим a0 и a1 и запишем уравнение оптимальной прямой:
![]()
Построим график функции p[t]:
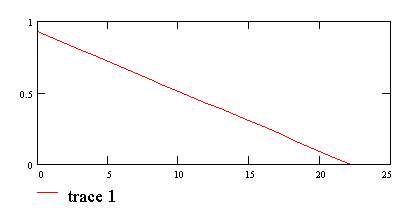
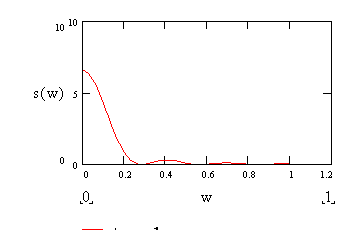
10. Вычислим нормированную спектральную плотность S(w):
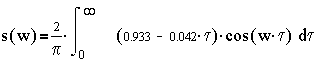
![]()
Похожие работы
... математического ожидания. Таким образом, (72.6) принимает вид . (72.7) 72.2. Функции вида , (72.8) где целые числа , называются начальными моментами порядка случайного процесса . Аналогично центральные моменты определяются соотношениями: . (72.9) Для функций (72.8), (72.9) используется общее название - моментные функции. Наиболее простые ...
... ≠ j) X(t) = mx(t) + ∑ Viφi(t) (t ? T) Следует: K(t, t’) = ∑ Diφi(t)φi(t’) Эту формулу называют каноническим разложением корреляционной функции случайного процесса. В случае уравнения X(t) = mx(t) + ∑ Viφi(t) (t ? T) Имеют место формулы: X(t) = mx(t) + ∑ Viφ(t) ∫ x(τ)dt = ∫ mx(τ)dτ + ∑ Vi ...
... и реализация оптимальных в определенном смысле свойств системы по заданным статистическим свойствам входных сигналов. Статистическая динамика является разделом теории управления и базируется на теории вероятности и, в частности, на ее разделе теории случайных процессов. 1.1 Основные понятия теории вероятности Рассмотрим случайные величины и их характеристики. Случайное событие – это событие ...
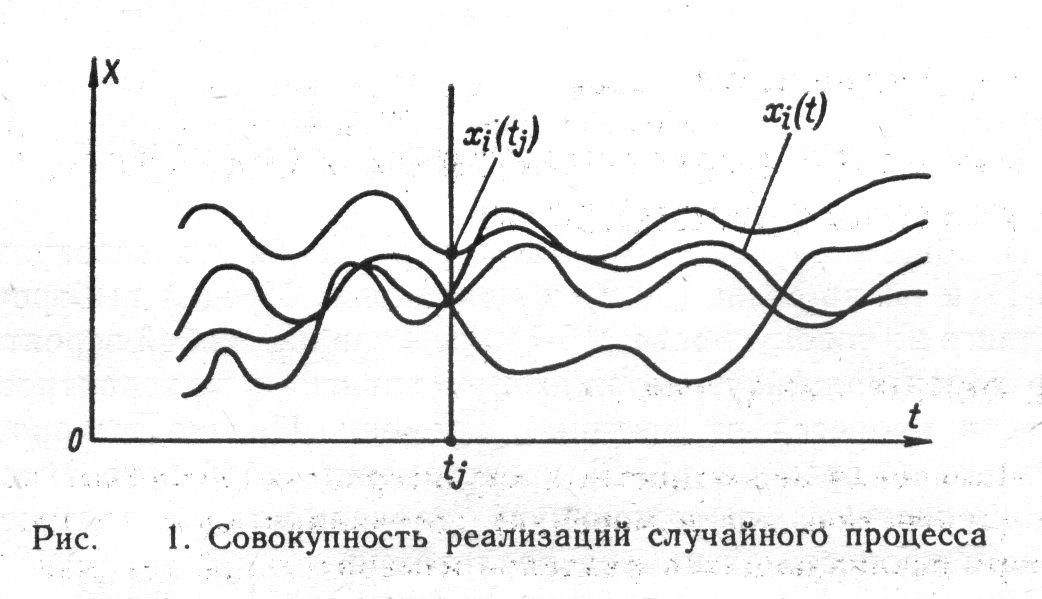
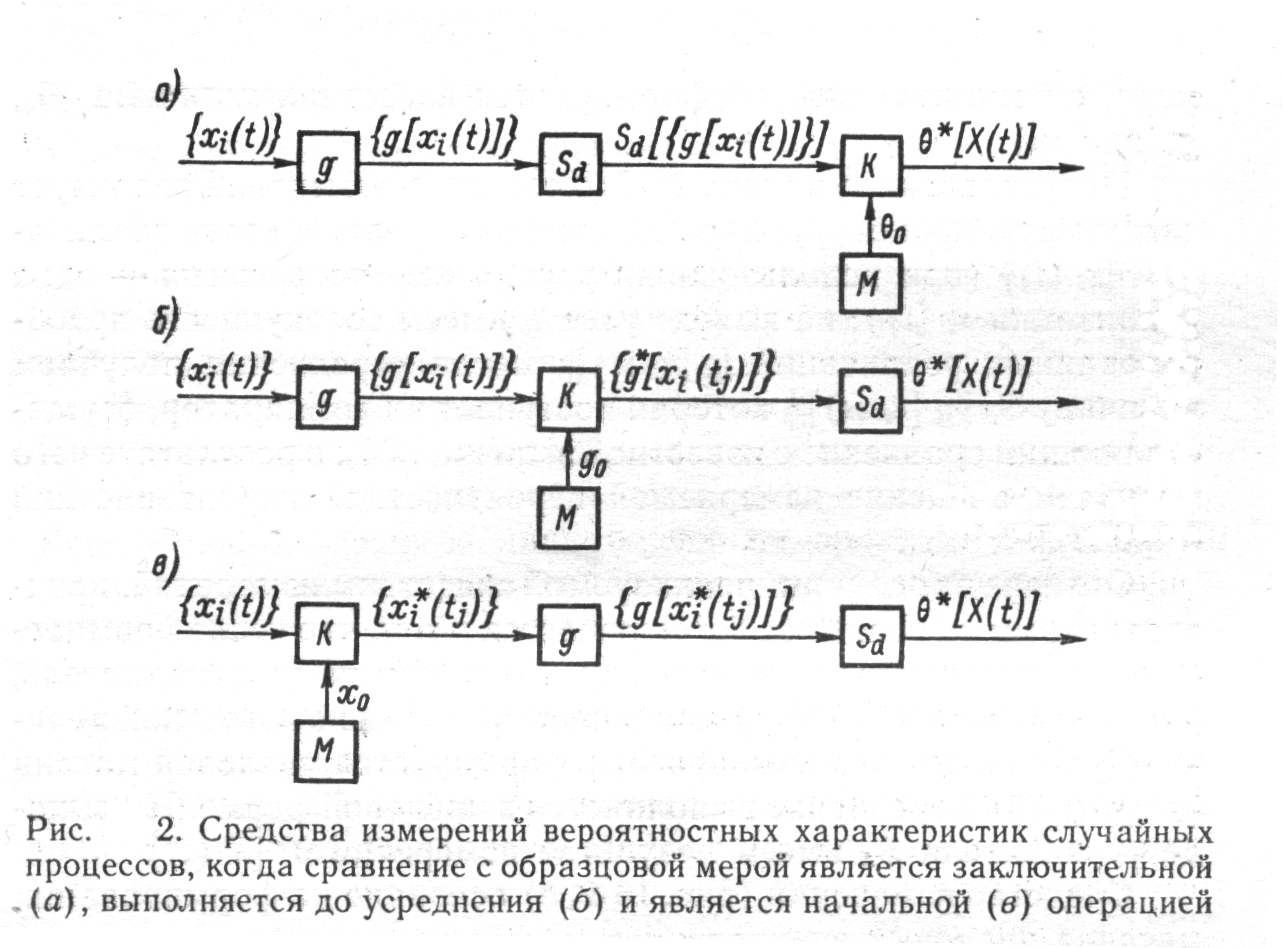
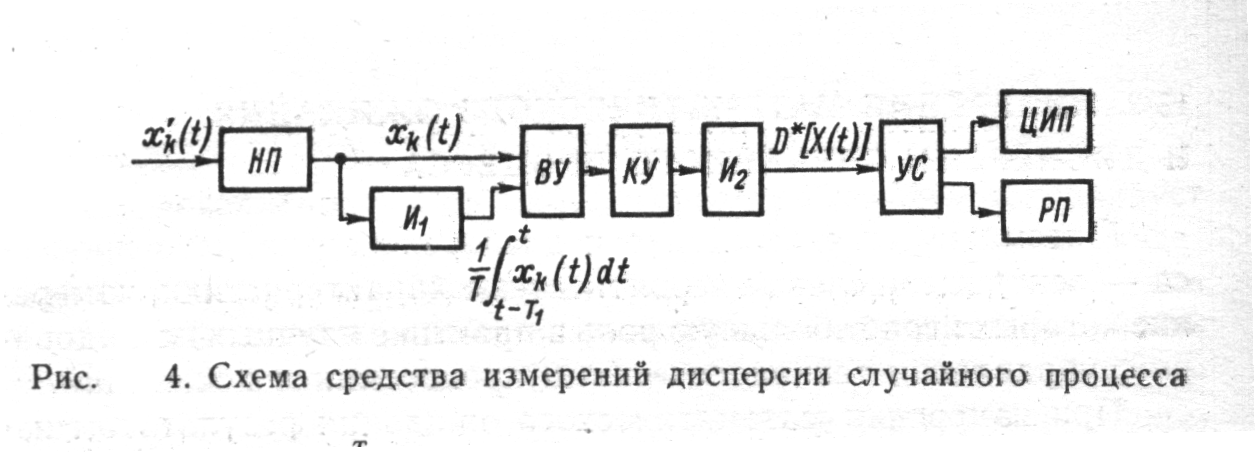
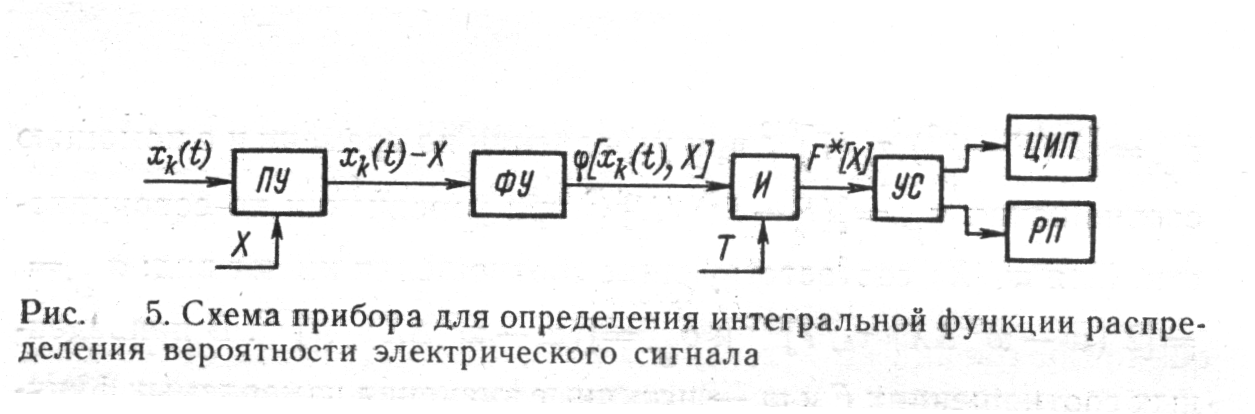
... описание производится с помощью систем вероятностных характеристик: многомерных функций распределения вероятности, моментных функций, характеристических функций и т. п. В теории статистических измерений исследуемый случайный процесс представляется своими реализациями, причем полное представление осуществляется с помощью так называемого ансамбля, т. е. бесконечной совокупностью реализаций. ...
0 комментариев