Навигация
2. ПРИНЦИП СИММЕТРИИ
“Насколько я могу судить, все априорные утверждения физики имеют своим источником симметрию”
Weyl H. Symmetry–Princeton: Princeton Universal Press,1952
2.1. Методология естествознания. В качестве методологической основы анализа геометрических идей в современном естествознании (в плане их применения в теориях пропорций) могут быть принципы, на которые Э.Шмутцер (21) указывает как на основные, для создания физической теории: принцип простоты (максимально полное описание с помощью минимального числа законов); принцип ковариантности (независимость законов, наполненных физическим содержанием от субъекта и произвольно выбираемых параметров системы отсчета); геометрические основы (возможен переход к геометрии с кручениями); квантовый характер (выход за рамки классических представлений); правила перестановок и динамические законы; симметрия; причинность; принцип непрерывности познания (законы на более высоком уровне включают нижние, как частные случаи). Исследование геометрических моделей в физике с позиции соблюдения принципа симметрии, и его преемственности при переходе с одних уровней на другие, может быть принято для анализа проблем геометрии архитектурных пропорций.
2.2. Принцип непрерывности познания. Принцип непрерывности познания предполагает естественный переход от старой теорий к новой, корректный ввод новых представлений и процедур преобразований, связанных с математическим переоформлением прошлого знания. Анализируя проблемы геометрии релятивистской физики ХХ века и следуя принципу непрерывности в познании, мы должны: 1) вернуться к той исторической ситуации, когда была создана теория относительности; 2) к причинам отрицания СТО и разработки ОТО; 3) к тому фундаментальному открытию, которое привело к отрицанию абсолютной системы отсчета Ньютона - к открытию конечной величины скорости света.
2.3. Принцип симметрии. Принцип симметрии один из ведущих принципов познания. Он лежит в фундаменте диалектики. Законы единства и борьбы противоположностей по существу отражают основной закон симметрии связанный с различием и тождеством диалектических сторон явления, составляющих сущность его движения, развития.
Пьер Кюри рассматривал симметрию как результат диалектического взаимодействия объекта со средой. Он придавал симметрии огромную роль в исследовании физических явлений: “Думаю, что представляет интерес ввести в изучение физических явлений понятие о симметрии, столь привычной кристаллографам” (Пьер Кюри, 1894г. “О симметрии физических явлений; симметрии электрического и магнитного поля”). По Кюри, симметрия порождающей среды накладывается на симметрию тела, образующегося в этой среде. Получившаяся в результате форма тела сохраняет только те элементы собственной симметрии, которые совпадают с наложенными на него элементами среды, т.е. сохраняются только тождественные свойства (среда, тело–диалектические противоположности, порожденный объект - их единство).
Понятие симметрии, развиваемое Пьером Кюри, шире обыденного понимания симметрии как, например, зеркальное равновесие масс, и предполагает, прежде всего, симметрию как движение, как развитие, как отношение отрицания единичных свойств тела и среды и утверждения их общих свойств в форме особенного, порожденного ими нового тела (2,10,18). Другим примером динамической симметрии является процесс метаболизма, свойственный органическим формам, как единство синтеза и распада. При очевидном различии (жизнь и смерть), эти процессы находятся в отношении симметрии.
В научной методологии, смысл симметрии (отношений) так же предполагает, что фундаментальный закон должен быть инвариантным по отношению к действию некоторой операции симметрии (преобразования координат, функциональные преобразования и т.п.).
3. СИММЕТРИЯ В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
3.1. Геометрия специальной теории относительности. Соответствует ли принципам симметрии модель пространства-времени, разработанная специальной теорией относительности с целью органичного включения открытой физической постоянной – скорости света в физическую теорию, взамен представлениям Ньютона, об отсутствии ограничений на скорость?
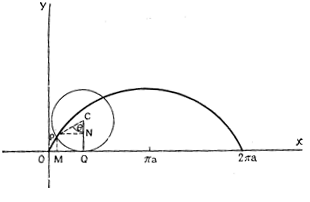
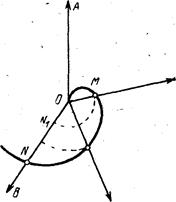
Геометрическим способом введения в физику световой константы и светоподобного интервала является псевдоевклидова геометрия (теорема Пифагора, связывающая в псевдоевклидовой метрике абсолютный и относительные интервалы пространства и времени). Пространство-время представлено ортогональными координатами и разделено образующими, для которых x = t (это взаимно-перпендикулярные, развернутые вокруг центра системы отсчета (x,t) под углом ![]() образующие (ct,-ct). Они разделяют ИСО на две области: область до световых скоростей и область сверхсветовых скоростей. Область до световых скоростей, в свою очередь, состоит из области прошлого и области будущего (Рис.1). Квадрат абсолютного интервала равен разности квадратов относительных интервалов пространства и времени:
образующие (ct,-ct). Они разделяют ИСО на две области: область до световых скоростей и область сверхсветовых скоростей. Область до световых скоростей, в свою очередь, состоит из области прошлого и области будущего (Рис.1). Квадрат абсолютного интервала равен разности квадратов относительных интервалов пространства и времени: ,
,![]() .
.
3.2. Нарушение принципа симметрии специальной теорией относительности. Отметим следующие нарушения принципа симметрии в модели ИСО СТО:
1. Кроме скорости v (абсолютной скорости пробной частицы), и скорости с (абсолютной скорости света), в уравнениях присутствует скорость![]() , физический смысл которой не ясен, кроме того, что она входит в выражение коэффициента Лоренцева сокращения (расширения)
, физический смысл которой не ясен, кроме того, что она входит в выражение коэффициента Лоренцева сокращения (расширения) . Как производная абсолютных скоростей v и c, она должна иметь аналогичный смысл и указывает на существование некоторого реального физического объекта, с движением которого она связана.
. Как производная абсолютных скоростей v и c, она должна иметь аналогичный смысл и указывает на существование некоторого реального физического объекта, с движением которого она связана.
2. При ![]() равноправной v и c, отношения c/c = 1/1 = 1 и c/v = 1/
равноправной v и c, отношения c/c = 1/1 = 1 и c/v = 1/ так же должны иметь смысл адекватный смыслу
так же должны иметь смысл адекватный смыслу![]() . Иначе, предположительно, в световой модели Вселенной должны существовать три типа равноправных ИСО, со своими коэффициентами сокращения (расширения).
. Иначе, предположительно, в световой модели Вселенной должны существовать три типа равноправных ИСО, со своими коэффициентами сокращения (расширения).
3. Введение понятия светоподобного интервала, в связи с открытием в природе предельной скорости света (граничные параметры скоростей v=0, v=c), предполагает два типа равноправных ИСО, для которых состояние покоя формулируется относительно граничных параметров скорости света: , состояние покоя которой соответствует скорости v=0 (система отсчета Лоренца-Минковского в СТО) и
, состояние покоя которой соответствует скорости v=0 (система отсчета Лоренца-Минковского в СТО) и![]() , состояние покоя которой соответствует скорости света (фотон, как покоящаяся система). СТО не рассматривает такую равноправную
, состояние покоя которой соответствует скорости света (фотон, как покоящаяся система). СТО не рассматривает такую равноправную![]() . При заданном условии покоя v=c),
. При заданном условии покоя v=c),  покоится на образующих светоподобного конуса (сt ,-ct) на таких же законных основаниях как
покоится на образующих светоподобного конуса (сt ,-ct) на таких же законных основаниях как ![]() покоится при v=0.
покоится при v=0.  зеркальна
зеркальна![]() . Если
. Если  расширяется, то
расширяется, то![]() – сокращается. Скорость частицы в
– сокращается. Скорость частицы в  -
-![]() ,
,  = c/v=
= c/v=![]() . Так как - v в
. Так как - v в  и
и ![]() в
в  связаны скоростью света (или светоподобным интервалом),
связаны скоростью света (или светоподобным интервалом),  и
и ![]() являются относительными, связанными между собой светоподобным интервалом, подсистемами одной и той же системы отсчета. Иначе, светоподобный интервал это не только предельная величина скорости, что утверждает СТО, но, прежде всего, скорость, связывающая две равноправные, но качественно различные ИСО покоя в движении одной и той же “пробной массы”, т.е. системы отсчета присущих ей различных форм движения, например, как частицы - v и как излучения -
являются относительными, связанными между собой светоподобным интервалом, подсистемами одной и той же системы отсчета. Иначе, светоподобный интервал это не только предельная величина скорости, что утверждает СТО, но, прежде всего, скорость, связывающая две равноправные, но качественно различные ИСО покоя в движении одной и той же “пробной массы”, т.е. системы отсчета присущих ей различных форм движения, например, как частицы - v и как излучения - . Эти скорости могут быть связаны с различной плотностью массы пробной частицы (например, v – скорость положительной плотности +p и
. Эти скорости могут быть связаны с различной плотностью массы пробной частицы (например, v – скорость положительной плотности +p и ![]() - скорость отрицательной плотности -p).
- скорость отрицательной плотности -p).
4. В связи с тем, что в ИСО Минковского часть пространства-времени связана с досветовыми скоростями (конуса будущего и прошлого), а часть - со сверхсветовыми скоростями, она не только полностью не определена, но допускает нарушение исходного принципа своей конструкции – движение со сверхсветовой скоростью. Если допустить существование сверхсветовых скоростей, мы, при конструировании ИСО, должны отказаться от скорости света, связанного с ней  и определяться в новом геометрическом принципе ИСО. Но это уже будет совершенно другая система отсчета.
и определяться в новом геометрическом принципе ИСО. Но это уже будет совершенно другая система отсчета.
5. В уравнении закона сохранения (например, для абсолютного интервала массы покоя ):
):
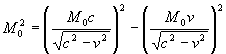 1)
1)
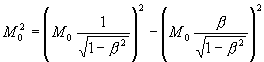
![]() 2)
2)
Где ![]() - абсолютный интервал t-подобной массы покоя
- абсолютный интервал t-подобной массы покоя
![]() - относительный интервал t-подобной энергии;
- относительный интервал t-подобной энергии;
![]() - относительный интервал x-подобного импульса
- относительный интервал x-подобного импульса
об абсолютной природе интервала ![]() можно говорить лишь в относительном смысле, в связи с применением
можно говорить лишь в относительном смысле, в связи с применением![]() , так как по аналогии с правой частью равенств 1) и 2), абсолютный интервал в левой части равенства, может быть выражен в форме
, так как по аналогии с правой частью равенств 1) и 2), абсолютный интервал в левой части равенства, может быть выражен в форме . Интервал абсолютен только при
. Интервал абсолютен только при![]() .
.
Поскольку 1/1, 1/![]() не могут рассматриваться иначе, как равноправные
не могут рассматриваться иначе, как равноправные  (наравне с
(наравне с![]() ), ясно, что масса покоя 1),2) теряет свой абсолютный смысл, если ее рассматривать относительно
), ясно, что масса покоя 1),2) теряет свой абсолютный смысл, если ее рассматривать относительно  = 1/
= 1/![]() или
или  = 1/1, т.е. представление абсолютности интервала 2) справедливо лишь при
= 1/1, т.е. представление абсолютности интервала 2) справедливо лишь при .
.
3.3. Незавершенность геометрии ИСО в СТО. Внутренние (нарушение симметрии в уравнении скоростей, наличие несистемных областей пространства-времени) и внешние (независимость системы отсчета от материи, неточность отражения движения в связи с гравитационными эффектами) противоречия ИСО в СТО, необоснованность выражения пространственно-временного континуума теоремой Пифагора в связи с принципиально различной природой пространства (как протяженной характеристики) и времени (как длительной характеристики), позволяют сделать вывод, что ограниченность ИСО в СТО связана, прежде всего, с незавершенностью, неразвернутостью геометрии ее координатного пространства.
Похожие работы
... различных видах деятельности; • развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; • формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; • ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и ...
... философия (основные положения, проблемы, понятия).} 21. ФИЛОСОФИЯ ЭКЗИСТЕНЦИАЛИСТОВ. (Камю. "Миф и Сизифе. Эссе об абсурде", Сартр. "Экзистенциализм - это гуманизм"). Экзистенциализм - Философия существования. Иррационалистическая фил. Наиболее крупные представители: М. Хейдеггер, религиозный( К Ясперс, Г.Марсель, ) атеистический (Ж.П.Сартр, А.Камю), Н.Аббаньяно. В Герм э. ...
... методология исследования биологических циклов. В этой связи можно указать на работы ученого из Ставрополя профессора Гневушева В.В. В своих работах Гневушев В.В. активно использует общую теорию циклов и выходит на совершенно оригинальные и неожиданные результаты. Исследования хронобиологов не могут не использоваться в современной медицине. Процесс циклизации медицины в самом широком смысле уже ...
... и более живой. Хотя простейший из изучаемых уровней самоорганизации - это уровень диссипативных структур, образованных в самообновляющихся химических реакциях, применение этих принципов к биологическим, психологическим и социологическим явлениям нельзя назвать редукционистским мышлением. В отличие от редукционизма в механистической науке такие интерпретации основаны на фундаментальной гомологии, ...

0 комментариев