Навигация
ОСНОВНЫЕ СВОЙСТВА АБСОЛЮТНОЙ СИСТЕМЫ ОТСЧЕТА
89841
знак
0
таблиц
6
изображений
5. ОСНОВНЫЕ СВОЙСТВА АБСОЛЮТНОЙ СИСТЕМЫ ОТСЧЕТА.
5.1. Абсолютная система отсчета (
) является следствием соединения принятой в СТО 
(покой при v=0) и не выявленной в СТО 
(покой при v=c). Каждая ИСО представлена одной осью (нормалью или касательной) в соприкасающейся плоскости трехгранника Френе. Обе ИСО взаимно ортогональны. Результирующая 
представлена на бинормали и является следствием векторного произведения на. С другой стороны, мнимые и действительные, положительные и отрицательные моменты в соприкасающейся плоскости трехгранника Френе являются следствием квадратичного разложения бинормальных моментов. С мнимыми моментами могут быть связаны различные "виртуальные" эффекты (например, когда действительный бинормальный момент распадается на два мнимых момента). Координатные оси имеют переменную сигнатуру в зависимости от знака направления оси. В связи с вышесказанным, результирующая система отсчета может рассматриваться или как бинормаль, или как эквивалентная ей соприкасающаяся плоскость, что, безусловно, определяет ее специфику (т.е. дуализм) и может быть связано с различными, существенными в физике, эффектами.
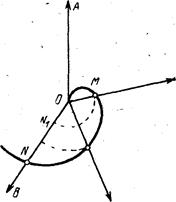
5.2. имеет ортогональную 6-мерную систему пространства кручений. Мнимый и действительный трехгранники Френе, по положительным и отрицательным направлениям касательной и нормали, связаны абсолютными осевыми интервалами (принятым в СТО уравнением 4-мерного пространственно-временного континуума, но не для трансляций, а для 3-мерных, x-подобных и 1-мерных, t-подобных, противоположных по направлению, моментов инерции. О пространстве-времени мы говорим условно, имея в виду различие в метрике (как между 3-мерной касательной скоростью и 1-мерной нормальной скоростью).
5.3. Геометрия включает три взаимосвязанных на афинной плоскости геометрии: геометрия Минковского (М-геометрия), геометрия Евклида (Е-геометрия), геометрия Галилея (Г-геометрия). Для этих геометрий действительны: аксиома о параллельных прямых, определение координатного пространства (ортогональная система), определение расстояний (теорема Пифагора). Можно говорить о том, чтосинтезирует три А-геометрии в целостную геометрическую систему - МЕГа – геометрию (4). В частности, положительные и отрицательные осевые моменты в соприкасающейся плоскости связаны абсолютными светоподобными моментами в М-геометрии; относительные, нормальные и касательные “левые” моменты связаны абсолютным x-подобным моментом в Е-геометрии; нормальные и касательные “правые” моменты связаны абсолютным t-подобным моментом в Е-геометрии; положительные и отрицательные бинормальные моменты связаны абсолютным бинормальным моментом в Г-геометрии. Е-геометрия и М-геометрия являются следствием векторного разложением Г-геометрии.
5.4. Система координат остается ортогональной для всех состояний инерциального движения 
(в отличии от координат пространства-времени ИСО ОТО, где действительные кручения массы пробной частицы перенесены на мнимые преобразования (повороты) координатных осей при изменении скорости. В связи с отсутствием гравитационных эффектов (пробная частица адекватна всей области координатного пространства) и отсутствием ограничений на величину пробной массы частицы (сняты ограничения гравитации), предполагает принципиально новое и отличное от ИСО СТО определение инерциального движения (например, в отличии от 14). В частности, в геометрии кручений теряет смысл трансляционная метрика, а движение (изменение скорости) связывается с изменением состояния (плотности, размера) пробной частицы, без ограничений на ее массу.
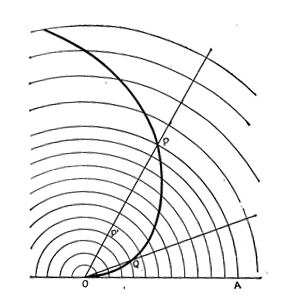
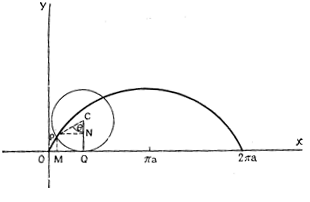
5.5. Инерциальное самодвижение в является следствием противодействия положительной и отрицательной плотности (экстремум при = 1 и 
= 0 в I и III четвертях единичной окружности, рис.2), с одной стороны, и противодействия результирующих x-подобного (левого) и t-подобного (правого) моментов инерции (экстремум при = 
во II и IV четвертях рис.2). Поскольку состояние покоя плотности связано с максимальной энергией кручений (энергия - как скалярное произведение x-подобных на t-подобные моменты) и, наоборот, состояние покоя кручений связано с максимальной энергией плотности (энергия - как векторное произведение x-подобных и t-подобных моментов), самодвижение в - результат противодействия энергии плотности и энергии кручений.
5.6. Включение в ИСО мнимых величин позволяет приблизиться к новому пониманию природы сил инерции и по новому ставит диалектику отношений внутреннего и внешнего. В частности, действительный, но отрицательный бинормальный момент, распадающийся на два мнимых момента в соприкасающейся плоскости, по форме является “внешней силой”, по отношению к действительным моментам в соприкасающейся плоскости, как “внутренним силам”. В связи с этим, законы сохранения интервалов в замкнутой, связывающие мнимые и действительные моменты, могут рассматриваться как уравнения внешних и внутренних сил инерции изолированной системы. Самодвижение есть следствие взаимодействия собственных “внешних” и “внутренних” сил изолированной пробной массы. Отношения равновесия (сохранения количества движения) самодвижения, могут рассматриваться в форме столкновения энергий (масс) положительной и отрицательной плотности.
5.7. Инерциальное самодвижение может быть связано, как с представлениями Ньютона (21), который утверждал, что центробежная сила, в отличии от прочих сил, берет свое начало в абсолютно пустом пространстве, так и с представлениями Э.Маха (“принцип Маха”), который считал, что космические массы (“далекие массы”) создают, после усреднения их относительных движений, выделенную систему отсчета (космическую систему Маха), и которая принимается нами за абсолютно существующее пространство (21). Позиции Ньютона и Маха близки развиваемой концепции в том смысле, что предполагают существование некоторых мнимых, "внешних" сил, необходимо связанных с действительным движением.
5.8. Инерциальное самодвижение может быть связано с некоторыми следствиями теории физического вакуума Г.И.Шипова. В частности, решения уравнений, описывающих вакуумное возбуждение без массы и заряда, но обладающие трехмерным спином. Как указывает Шипов: “Поля, имеющие нулевую энергию, но способные к взаимодействию (например вращать плоскость поляризации света) в физике встречаются впервые, поэтому при их изучении надо быть готовым к неожиданным физическим эффектам. Например, потенциальная энергия взаимодействия решения уравнения равна нулю, однако “вращательная траектория” материальной частицы, подчиняющаяся уравнениям движения, будет меняться, передавая “вращательную” информацию. Такие поля можно было бы определить как информационные поля, переносящие торсионную информацию о физическом объекте” (22 с.188)
5.9. 6-мерное пространство кручений, отсутствие трансляционной метрики указывает на то что, система отсчета описывает среды, отличные от твердых тел. Это могут быть упругие среды (в квантовой теории поля – физический вакуум). Если связана с физическим вакуумом, что очень вероятно при ее исключительно торсионной геометрии, то абсолютный физический вакуум следует определять как неквантованное состояние первоматерии, без ограничений на плотность, в отличие от традиционного понимания (предельно растянутая материя, пустота). В соответствии EGS-концепцией А.Акимова (22), можно предполагать связь трех принципиальных форм закона сохранения в с основными поляризационными состояниями вакуума - по осям нормали и касательной - гравитационная поляризация, с t-подобными (II четверть) и x-подобными моментами (IV четверть) – электрон-позитронная поляризация, с бинормальными моментами - торсионная поляризация. Связи этих состояний поляризации может так же рассматриваться в контексте отмеченной выше связи между геометриями Галилея, Евклида и Минковского.
5.10. Уравнения инерциального движения однозначно определены на всем диапазоне скоростей, поддаются полной геометризации (взаимное сокращение массы в правой и левой частях равенства). Пространство моментов энергий импульсов может рассматриваться в отношениях 6-мерного векторного пространства кручений сферы единичного радиуса для единичной массы (мнимая, действительная и комплексная геометрии с угловыми скоростями, представленными тригонометрическими функциями). Философское и математическое содержание развиваемой идеи симметрии связано с качественно новым математическим определением понятия точки. Традиционное определение точки, связанное с трансляционными преобразованиями пространства в точку (объем – плоскость – линия - точка), отражают лишь относительное изменение масштаба, но не вносят в определение точки нового качества, отличного от трехмерного пространства. Как бы мы ни старались описывать точку, как некоторую микроскопическую величину, ее трехмерная природа сохраняется, она не может быть выделена как новое качество никакими изменениями “калибра”. В новом смысле, точка определяется в безразмерном 6-мерном пространстве кручений, связанном действительной, мнимой и комплексной системой геометрий на Афинной плоскости (геометрии Евклида, Галилея, Минковского). Дальнейшая трансформация точки в трехмерное пространство теперь связана не с ее трехмерными трансляциями вовне, а с внутренним процессом ее деления (квантования). В мире кручений физика и геометрия адекватны и геометрия выступает как абсолютная система идеально геометризированных физических уравнений, соответствующих природе материи.
5.11. Очевидно, что, взятая относительно и 
, приводится обратным путем (с учетом явлений связанных с зеркальной симметрией и комплексным трехгранником Френе) в относительные ИСО СТО, с преобразованием абсолютных интервалов в относительные и наоборот, относительных в абсолютные. Геометрия относительных, локальных ИСО будет связана с применением коэффициентов расширения (сокращения). Но относительно, расширение или сокращение локальных ИСО будет иметь мнимую форму (подобно “мнимым” киноэффектам при монтаже сказочных фильмов с превращениями карликов в великанов, и, наоборот, благодаря изменению масштаба, калибра окружающего ландшафта). С учетом эффектов зеркальной симметрии, уравнения инвариантны уравнениям ИСО СТО, или другим физическим уравнениям, которые включают 4-мерный пространственно-временной континуум ИСО СТО. Вероятно, что 6-мерная торсионная геометрия, согласуется с торсионными координатами Г.И.Шипова (с 6-ю угловыми координатами - тремя пространственными углами
и тремя псевдоевклидовыми углами - 10-мерного пространства событий произвольно ускоренных четырехмерных систем отсчета) концепции физического вакуума).
5.12. Преобразование ИСО СТО переводит ее с частного случая ОТО в абсолютную, всеобщую систему отсчета. изначально лежит в основе общего принципа относительности Эйнштейна, объявляющего равноправность локальных, ускоренных инерциальных систем отсчета, является его обоснованием (как и обоснованием геометризации уравнений материи ОТО). в качественно новой форме утверждает принципы классической механики. Являясь синтетической основой соединения математики и естественно-научного знания, (в основе симметрии которой лежат диалектические противоположности – “правое-левое”, “положительное-отрицательное” - и их тождество, разрешаемое в законах сохранения интервалов), является системообразующей моделью для философского познания природы в категориях и законах диалектики. Иначе, развитие развиваемой концепции симметрии, в перспективе, предполагает новый уровень понимания природы, в основе которого лежит гармоничный синтез математики, философии и естествознания.
Похожие работы
... различных видах деятельности; • развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; • формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; • ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и ...
... философия (основные положения, проблемы, понятия).} 21. ФИЛОСОФИЯ ЭКЗИСТЕНЦИАЛИСТОВ. (Камю. "Миф и Сизифе. Эссе об абсурде", Сартр. "Экзистенциализм - это гуманизм"). Экзистенциализм - Философия существования. Иррационалистическая фил. Наиболее крупные представители: М. Хейдеггер, религиозный( К Ясперс, Г.Марсель, ) атеистический (Ж.П.Сартр, А.Камю), Н.Аббаньяно. В Герм э. ...
... методология исследования биологических циклов. В этой связи можно указать на работы ученого из Ставрополя профессора Гневушева В.В. В своих работах Гневушев В.В. активно использует общую теорию циклов и выходит на совершенно оригинальные и неожиданные результаты. Исследования хронобиологов не могут не использоваться в современной медицине. Процесс циклизации медицины в самом широком смысле уже ...
... и более живой. Хотя простейший из изучаемых уровней самоорганизации - это уровень диссипативных структур, образованных в самообновляющихся химических реакциях, применение этих принципов к биологическим, психологическим и социологическим явлениям нельзя назвать редукционистским мышлением. В отличие от редукционизма в механистической науке такие интерпретации основаны на фундаментальной гомологии, ...
0 комментариев