Навигация
Конспекты лекций по математической логике.
1. Теория алгоритмов
1.1 Различные подходы к определению алгоритма:
10. Неформальное понятие алгоритма (последовательность инструкций для выполнения действия).
20. Машина с неограниченными регистрами (МНР).
30 Машина Тьюринга – Поста (МТ-П).
40 Нормальные алгоритмы Маркова (НАМ).
1.1.1 Машина с неограниченными регистрами (МНР).
![]() Имеется некое устройство, в котором счетное число ячеек памяти (регистров), в которых хранятся целые числа.
Имеется некое устройство, в котором счетное число ячеек памяти (регистров), в которых хранятся целые числа.
Допустимые команды:
Z(n) - обнуление регистра Rn.
S(n) - увеличение числа в регистре Rnна 1.
T(m,n) - копирует содержимое Rm в регистор Rn.
I(p,q,n) - если содержимое Rp = Rq то выполняется команда с номером n , если нет
следующая.
Программа для МНР должна быть последовательностью команд Z, S, T, I с определенным порядком, выполняемые последовательно.
Тезис Черча (Churcha): Первое и второе определение алгоритма эквивалентны между собой. Любой неформальный алгоритм может быть представлен в программе для МНР.
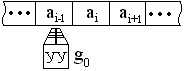 1.1.2 Машина Тьюринга - Поста.
1.1.2 Машина Тьюринга - Поста.
Имеется устройство просматривающее бесконечную ленту, где есть ячейки содержащие элементы алфавита: ![]() , где
, где ![]() - пустой символ (пустое слово), который может принадлежать и не принадлежать А. Также существует управляющая головка (устройство) (УУ)/(УГ), которая в начальный момент расположена в определенном месте, в состоянии
- пустой символ (пустое слово), который может принадлежать и не принадлежать А. Также существует управляющая головка (устройство) (УУ)/(УГ), которая в начальный момент расположена в определенном месте, в состоянии ![]() . Также существуют внутренние состояния машины:
. Также существуют внутренние состояния машины: ![]()
Слово в данном алфавите - любая конечная упорядоченная последовательность букв данного алфавита, притом длина слова это количество букв в нем (у пустого слова длина 0).
Допустимые команды:
| 1) 2) | Последовательность команд называется программой, если в этой последовательности не встречается команд с одинаковыми левыми частями. Машина останавливается если она не находит команды с левой частью подобной текущей. |
1.1.3 Нормальные алгоритмы Маркова.
Тип машины перерабатывающий слова, в которой существует некий алфавит ![]() , для которого W - множество всех слов.
, для которого W - множество всех слов.
Допустимые команды: (Для машин этого типа важна последовательность команд.)
|
| Пример: Программа:
|
1.1.4 Реализация функции натурального переменного. ![]()
![]() но мы допускаем не всюду определенную функцию.
но мы допускаем не всюду определенную функцию.
![]()
![]()
![]() то это означает, что
то это означает, что ![]()
притом ![]() , если f не определена, то и программа не должна ничего выдавать.
, если f не определена, то и программа не должна ничего выдавать.
![]()
![]()
![]()
![]()
![]()
![]()
притом ![]() , если f не определена, то и программа не должна ничего выдавать.
, если f не определена, то и программа не должна ничего выдавать.
(![]() , а числа представляются в виде
, а числа представляются в виде ![]() ,например
,например ![]() .)
.)
Похожие работы
... утверждают или отрицают какие-либо отношения между объектами и явлениями реальной действительности. 3.Математическая логика и «Здравый смысл» в XXI веке. Логика - не только сугубо математическая, но также и философская наука. В XX веке эти две взаимосвязанные ипостаси логики оказались разведенными в разные стороны. С одной стороны логика понимается как наука о законах правильного мышления, ...
... занимательности. Упражнения однотипны. Поэтому просто необходимо дополнять данные в учебнике упражнения дополнительными заданиями развивающего характера. Глава II. Методика изучения элементов алгебры и математической логики. § 1. Методика изучения числовых выражений, выражений с переменными, числовых равенств и неравенств, уравнений. Изучение числовых выражений, равенств и неравенств, а ...
... утверждение "Я никогда не пользуюсь методами математической логики". Очевидно, что они противоречат друг другу, однако они вполне могут оказаться одновременно ложными. Например, если вы специалист по математической логике, то вы должны часто пользоваться её методами, но вряд ли они нужны вам каждый день вашей жизни. Закон исключенного третьего предназначен для использовании в области точных наук, ...
... постулаты D (то есть аксиомы Ax Ì FÍ A* и дедуктивные средства P Ì Fn+1), то говорят о построении теории как формальной системы F.S. = <L, D> = <A, S, Ax, P>Þ <A, F, Ax, P>. Другим подходом к построению математической логике является - содержательный, то есть неформальный. В этом случае аксиомы и дедуктивные средства явным образом не определяются (то есть ...
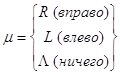 .
.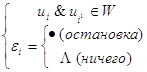
0 комментариев