Навигация
3.1.4 Теорема Дедукции.
Если из
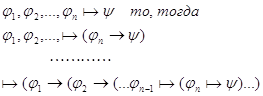
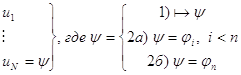
1) и 2а) 
, где 
по правилу m.p. 
, ч.т.д.
2б)
- уже выводили 
, ч.т.д.
Базис индукции: N=1 
- формальный вывод из длинного списка 
(только что доказано), осуществим переход по индукции:
по индукции
и по лемме 2
Пример: 
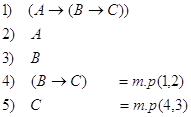по теореме дедукции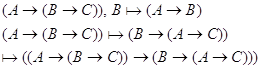 
3.2 Критерий выводимости в ИВ.
3.2.1 Формулировка теоремы.
- тавтология
при любой интерпретации алфавита (символов переменных)
3.2.2 Понятие интерпретации.
символ переменной 
переменную поставим в соответствие.
, где 
- проекция на 
.
; 
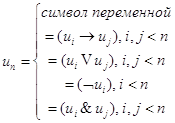
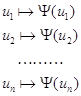- только символ
переменных, т.к.
это заглавное слово
формативной последо-
вательности вида:
Где: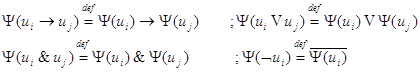 
3.2.3 Доказательство теоремы.
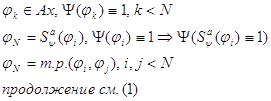
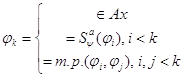формальный
вывод 
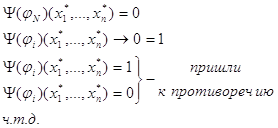
(1) 
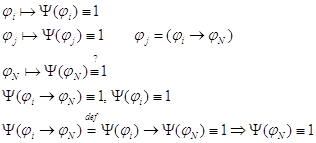
3.3 Непротиворечивость ИВ.
3.3.1 Определение.
1) ИВ противоречиво, если формула А выводима в нем. 
.
2) 
формула выводима в ИВ)
ИВ противоречиво.
3) 
ИВ противоречиво.
ИВ непротиворечиво, если оно не является противоречивым.
Теорема: ИВ является непротиворечивым исчислением по отношению к любому из трех определений.
Док-во: (1) Если 
, то соответствующая ей булева функция будет тождественно равна 1. 
(2) Если любая формула выводима, то выводима и А, что соответствует пункту 1.
(3)
Пусть 
и 
- булева функция
- противоречие.
Похожие работы
... утверждают или отрицают какие-либо отношения между объектами и явлениями реальной действительности. 3.Математическая логика и «Здравый смысл» в XXI веке. Логика - не только сугубо математическая, но также и философская наука. В XX веке эти две взаимосвязанные ипостаси логики оказались разведенными в разные стороны. С одной стороны логика понимается как наука о законах правильного мышления, ...
... занимательности. Упражнения однотипны. Поэтому просто необходимо дополнять данные в учебнике упражнения дополнительными заданиями развивающего характера. Глава II. Методика изучения элементов алгебры и математической логики. § 1. Методика изучения числовых выражений, выражений с переменными, числовых равенств и неравенств, уравнений. Изучение числовых выражений, равенств и неравенств, а ...
... утверждение "Я никогда не пользуюсь методами математической логики". Очевидно, что они противоречат друг другу, однако они вполне могут оказаться одновременно ложными. Например, если вы специалист по математической логике, то вы должны часто пользоваться её методами, но вряд ли они нужны вам каждый день вашей жизни. Закон исключенного третьего предназначен для использовании в области точных наук, ...
... постулаты D (то есть аксиомы Ax Ì FÍ A* и дедуктивные средства P Ì Fn+1), то говорят о построении теории как формальной системы F.S. = <L, D> = <A, S, Ax, P>Þ <A, F, Ax, P>. Другим подходом к построению математической логике является - содержательный, то есть неформальный. В этом случае аксиомы и дедуктивные средства явным образом не определяются (то есть ...
0 комментариев