Основоположником теории квадратичных форм является французский математик Лагранж. Им была доказана конечность числа классов бинарных квадратичных форм заданного дискриминанта.
Начинается арифметическая теория квадратичных форм с утверждения Ферма о существовании простых чисел ![]() суммой двух квадратов.
суммой двух квадратов.
Теория квадратичных форм продолжала развиваться. Гаусс также вводит много новых понятий. Гауссу сумел получить доказательства трудных и глубоких теорем теории чисел.
В данной работе исследуются предварительные общие сведения о бинарных квадратичных формах. Приведено элементарное доказательство известной оценки для числа приведенных неопределенных бинарных квадратичных форм заданного дискриминанта. Здесь рассмотрены периоды неопределенных квадратичных форм, также решены два вопроса о двусторонних формах. Также приведены доказательства, что диагональные формы одного и того же положительного дискриминанта не эквивалентны.
Предварительные сведения о бинарных квадратичных форм
Определим общие понятия и свойства, которые прямым образом касаются бинарных квадратичных форм.
Однородный многочлен второй степени от двух переменных называется бинарной квадратичной формой:
![]() (1)
(1)
где ![]() —вещественные числа.
—вещественные числа.
Соответственно используемые коэффициенты в данной формуле ![]() — являются первым, вторым и третьим коэффициентами .
— являются первым, вторым и третьим коэффициентами .
Для наглядности эту формулу будем обозначать через ![]() , получим:
, получим:
![]()
В теории форм над кольцами и в первую очередь над кольцом ![]() целых чисел более предпочтительной является запись вида (1).
целых чисел более предпочтительной является запись вида (1).
В теории квадратичных форм над полями приведены формы, у которых второй коэффициент без множителя ![]() , т. е.:
, т. е.:
![]()
Если в бинарной квадратичной форме (1) коэффициенты ![]() являются целыми числами, тогда эту форму называют классической целой или целочисленной по Гауссу.
являются целыми числами, тогда эту форму называют классической целой или целочисленной по Гауссу.
В данной работе классические квадратичные формы будем называть численными.
Если существует линейная подстановка переменных 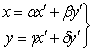 (2) с целыми коэффициентами
(2) с целыми коэффициентами ![]() и определителем
и определителем ![]() , переводящая форму
, переводящая форму ![]() в форму
в форму ![]() , такая, что выполняется равенство
, такая, что выполняется равенство
![]() , (3),
, (3),
тогда бинарные целочисленные квадратичные формы ![]() и
и ![]() называются собственно эквивалентными.
называются собственно эквивалентными.
Иначе, если целочисленная подстановка (2) с определителем ![]() переводит форму
переводит форму ![]() в форму
в форму ![]() , бинарные квадратичные формы называются несобственно-эквивалентными.
, бинарные квадратичные формы называются несобственно-эквивалентными.
Полученные эквивалентные формы обозначим следующим образом: ![]() ~
~ ![]()
Из (2) и (3) вытекают соотношения, связывающие коэффициенты двух эквивалентных форм ![]() и
и ![]() .
.
![]()
![]() (4)
(4)
![]()
Эквивалентные бинарные квадратичные формы имеют один и тот же дискриминант, т.е. число ![]() бинарной квадратичной формы
бинарной квадратичной формы ![]()
Предположим, что ![]() собственно или несобственно эквивалентна форме
собственно или несобственно эквивалентна форме ![]() . Значит, опираясь на определение об эквивалентности, можно сказать, что есть такие целые числа
. Значит, опираясь на определение об эквивалентности, можно сказать, что есть такие целые числа ![]() с определителем
с определителем ![]() , при которых выполняются соотношения (4). Отсюда следует:
, при которых выполняются соотношения (4). Отсюда следует:
![]()
Эквивалентные бинарные квадратичные формы представляют одно и то же множество целых чисел.
Допустим, что формы ![]() и
и ![]() эквивалентны. Значит, есть унимодулярная целочисленная подстановка переменных:
эквивалентны. Значит, есть унимодулярная целочисленная подстановка переменных:
![]()
![]() ,
,
тогда
![]()
Предположим ![]() , значит:
, значит:
![]() ,
,
Таким образом, форма ![]() — это есть число
— это есть число ![]() . В связи с тем, что отношение эквивалентности бинарных квадратичных форм имеет свойство симметричности, значит, любое число, которое выглядит, как
. В связи с тем, что отношение эквивалентности бинарных квадратичных форм имеет свойство симметричности, значит, любое число, которое выглядит, как ![]() можно заменить на
можно заменить на ![]() .
.
Свойствами рефлективности симметричности и транзитивности обладает отношение собственной эквивалентности бинарных квадратичных форм.
Следуя этому утверждению, можно сказать, что если для целого числа ![]() при некоторых целых
при некоторых целых ![]() и
и ![]() , а также для квадратичной формы
, а также для квадратичной формы ![]() выполняется равенство
выполняется равенство ![]() , значит, квадратичная форма
, значит, квадратичная форма ![]() представляет число
представляет число ![]() .
.
Множество всех бинарных квадратичных форм эквивалентных форме ![]() называют классом
называют классом ![]() форм.
форм.
В силу предложения 2 и определения 5 можно сказать, что множество бинарных квадратичных форм данного дискриминанта распадается на классы форм, собственно эквивалентных относительно унимодулярного целочисленного преобразования переменных (2).
Далее, в зависимости от знака дискриминанта ![]() , бинарные квадратичные формы делятся на определенные и неопределенные формы.
, бинарные квадратичные формы делятся на определенные и неопределенные формы.
Определение 6. Квадратичная форма ![]() дискриминанта
дискриминанта ![]() называется определенной, если
называется определенной, если ![]() и неопределенной, если
и неопределенной, если ![]() . Такое определение подсказано тем, что при
. Такое определение подсказано тем, что при ![]() бинарная квадратичная форма принимает значения только одного знака (положительные при
бинарная квадратичная форма принимает значения только одного знака (положительные при ![]() и отрицательные при
и отрицательные при ![]() ), а при
), а при ![]() она принимает как положительные, так и отрицательные значения. Теория неопределенных бинарных квадратичных форм существенно отличается от теории определенных форм, и мы будем рассматривать в данной работе только неопределенные формы.
она принимает как положительные, так и отрицательные значения. Теория неопределенных бинарных квадратичных форм существенно отличается от теории определенных форм, и мы будем рассматривать в данной работе только неопределенные формы.
Рассмотрим теперь вкратце теорию приведения неопределенных бинарных квадратичных форм. Суть этой теории состоит в выделении в каждом классе так называемых приведенных форм — «стандартных» форм класса. Рассматривая квадратичные формы положительного дискриминанта, будем считать ее коэффициенты произвольными вещественными числами. Кроме того, будем предполагать, что крайние коэффициенты ![]() и
и ![]() формы
формы ![]() отличны от нуля и корни уравнения
отличны от нуля и корни уравнения ![]() вещественны, различны и иррациональны.
вещественны, различны и иррациональны.
Назовем корень ![]() этого уравнения первым, а
этого уравнения первым, а ![]() — вторым корнем формы
— вторым корнем формы ![]() (см. [1]), причем
(см. [1]), причем ![]() есть дискриминант формы
есть дискриминант формы ![]() .
.
Определение 7. Неопределенная квадратичная форма
![]() с корнями
с корнями ![]() называется приведенной, если
называется приведенной, если ![]() .
.
Покажем, что у приведенной формы ![]() выполняются неравенства
выполняются неравенства ![]() ,
, ![]() , причем
, причем ![]() и
и ![]() заключаются между
заключаются между ![]() и
и ![]() . В самом деле, из условия
. В самом деле, из условия ![]() получаем
получаем
![]() ,
,
![]() ,
, ![]() ,
, ![]()
Далее, ![]() ,
, ![]() , т.е. выполняется указанное неравенство
, т.е. выполняется указанное неравенство ![]() . Обратимся теперь к условиям:
. Обратимся теперь к условиям:
![]() и
и ![]() . Из них следуют
. Из них следуют
![]() ,
, ![]() (*)
(*)
Аналогично имеем
![]() ,
, ![]() (**)
(**)
Покажем теперь, что ![]() . Допустим, что
. Допустим, что ![]() . Тогда из неравенств (*) и (**) следуют
. Тогда из неравенств (*) и (**) следуют
![]() и
и ![]()
Но последние два неравенства не могут одновременно выполняться. Значит, наше допущение, что ![]() неверно, и мы получаем неравенства
неверно, и мы получаем неравенства ![]() . Наконец, покажем, что
. Наконец, покажем, что
![]() и
и ![]()
Т.к. ![]() , то из неравенств (*) и (**) получаем
, то из неравенств (*) и (**) получаем ![]() . С учетом этих неравенств и равенства
. С учетом этих неравенств и равенства ![]() , мы получим и неравенства для
, мы получим и неравенства для ![]() .
.
Обратно, система неравенств
![]() или
или ![]()
характеризует приведенность неопределенной формы ![]() . Поэтому определению приведенной формы можно придать следующий вид.
. Поэтому определению приведенной формы можно придать следующий вид.
Определение 8. Бинарная квадратичная форма ![]() дискриминанта
дискриминанта ![]() называется приведенной, если
называется приведенной, если
![]()
или
![]()
Без доказательства приведем следующее свойство приведенных форм.
Предложение 4. Каждая форма дискриминанта ![]() собственно эквивалентна некоторой приведенной форме.
собственно эквивалентна некоторой приведенной форме.
Доказательство см. [1,2]. В [1] используется аппарат непрерывной дроби, а в [2] понятие соседней формы.
Определение 9. Целочисленная квадратичная форма ![]() называется собственно примитивной, если наибольший общий делитель ее коэффициентов равен
называется собственно примитивной, если наибольший общий делитель ее коэффициентов равен ![]() , т.е
, т.е
НОД ![]() и несобственно примитивной, если
и несобственно примитивной, если
НОД ![]() . В остальных случаях форма называется непримитивной.
. В остальных случаях форма называется непримитивной.
Определение 10. Пусть ![]() — наибольший общий делитель чисел
— наибольший общий делитель чисел ![]() для формы
для формы ![]() определителя
определителя ![]() . Множество бинарных квадратичных форм с одними и теми же
. Множество бинарных квадратичных форм с одними и теми же ![]() и (при
и (при ![]() ) с одним и тем же знаком крайних коэффициентов
) с одним и тем же знаком крайних коэффициентов ![]() называется порядком форм.
называется порядком форм.
Так как ![]() и знаки получающихся коэффициентов
и знаки получающихся коэффициентов ![]() при
при ![]() не меняются при переходе от данной формы к эквивалентной ей форме, то порядок состоит из нескольких классов.
не меняются при переходе от данной формы к эквивалентной ей форме, то порядок состоит из нескольких классов.
При ![]() формы и порядок называются собственно примитивными, а при
формы и порядок называются собственно примитивными, а при ![]() и
и ![]() (
( ![]() ) — несобственно примитивными. Собственно и классы форм называются собственно примитивными и несобственно примитивными.
) — несобственно примитивными. Собственно и классы форм называются собственно примитивными и несобственно примитивными.
Возникает вопрос: конечно или бесконечно число целочисленных приведенных неопределенных форм. Ответ дает следующее.
Предложение 5. Число всех целочисленных приведенных неопределенных форм с заданным дискриминантом конечно.
Доказательство см. [2,п.185]
О периодах неопределенных бинарных квадратичных уравнений
Теория неопределенных бинарных квадратичных форм существенно отличается от теории определенных форм наличием периодов приведенных форм. Гаусс первым обнаружил это явление и глубоко вник в природу приведенных форм с положительным неквадратным дискриминантом в связи с решением основных задач этой теории (см. [1,2]). В этом параграфе мы дадим основные свойства периодов неопределенных форм.
Нашему изложению мы сначала предпошлем те основные понятия из гауссовой теории квадратичных форм, которые нам понадобятся в дальнейшем (см. [1,2]).
Определение 1. формой соседней справа к целочисленной форме ![]() называется форма
называется форма ![]() , которая получается из формы
, которая получается из формы ![]() подстановкой
подстановкой 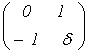 , где
, где ![]() — некоторое целое число.
— некоторое целое число.
Заметим, что при такой подстановке форма ![]() собственно эквивалентна форме
собственно эквивалентна форме ![]() . Зависимость между соседними формами
. Зависимость между соседними формами ![]() и
и ![]() можно охарактеризовать так: во-первых, формы
можно охарактеризовать так: во-первых, формы ![]() и
и ![]() имеют одинаковый дискриминант; во-вторых, последний коэффициент
имеют одинаковый дискриминант; во-вторых, последний коэффициент ![]() формы
формы ![]() является вместе с тем первым коэффициентом формы
является вместе с тем первым коэффициентом формы ![]() ; в третьих, сумма их средних коэффициентов
; в третьих, сумма их средних коэффициентов ![]() делится на
делится на ![]() .
.
Аналогичным образом определяется соседняя слева форма ![]() к форме
к форме ![]() .
.
Из определения соседних форм непосредственно следует предложение 1: соседние формы собственно эквивалентны.
С помощью процесса нахождения последовательных соседних форм мы придем к другому важному понятию периода приведенных форм. Именно, пусть ![]() — приведенная форма дискриминанта
— приведенная форма дискриминанта ![]() , и для нее
, и для нее ![]() является соседней справа; для
является соседней справа; для ![]() форма
форма ![]() является соседней справа; для
является соседней справа; для ![]() форма
форма ![]() является соседней справа и т.д. Тогда все формы
является соседней справа и т.д. Тогда все формы ![]() ,
, ![]() ,
, ![]() ,…, являются собственно эквивалентными между собой, так и форме
,…, являются собственно эквивалентными между собой, так и форме ![]() .
.
Так как в силу предложения 5 §1 число всех целочисленных приведенных неопределенных бинарных квадратичных форм с заданным дискриминантом конечно, то в бесконечном ряду форм ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,… не все формы могут быть различными между собой. Если предположить, что
,… не все формы могут быть различными между собой. Если предположить, что ![]() и
и ![]() совпадают, то формы
совпадают, то формы ![]() и
и ![]() будут приведенными соседними слева для одной и той же приведенной формы и потому будут совпадать. Поэтому
будут приведенными соседними слева для одной и той же приведенной формы и потому будут совпадать. Поэтому ![]() и
и ![]() и т.д. будут совпадать. Следовательно, в ряду
и т.д. будут совпадать. Следовательно, в ряду ![]() ,
, ![]() ,
, ![]() ,… обязательно повторится первая форма
,… обязательно повторится первая форма ![]() и если
и если ![]() — первая форма в этом ряду, совпадающая с
— первая форма в этом ряду, совпадающая с ![]() , то все формы
, то все формы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() различны между собой.
различны между собой.
Определение 2. Совокупность различных последовательных соседних приведенных неопределенных форм ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() называется периодом формы
называется периодом формы ![]() .
.
Приведем несколько общих замечаний об этих периодах, следующих из их определения (см. [2]).
Предложение 2. Если формы ![]() ,
, ![]() ,
, ![]() ,… представлены следующим образом
,… представлены следующим образом
![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() ,
, ![]() ,…, то все величины
,…, то все величины ![]() будут иметь одинаковые знаки, причем
будут иметь одинаковые знаки, причем ![]() все будут положительны.
все будут положительны.
Отсюда получается следующее свойство периодов.
Предложение 3. Количество квадратичных форм, из которых состоит период заданной формы ![]() , всегда четно.
, всегда четно.
Доказательство предложения 3 см. [1,2].
Заметим, что каждая форма ![]() , которая содержится в периоде формы
, которая содержится в периоде формы ![]() , будет иметь тот же период, что и
, будет иметь тот же период, что и ![]() .Именно, этот период будет таков:
.Именно, этот период будет таков:
![]()
Отсюда получается следующее свойство периодов.
Предложение 4. Все целочисленные неопределенные бинарные квадратичные формы с одинаковым дискриминантом могут быть разбиты на периоды.
Доказательство (см. [2] разд. V , п.187) основано на том их свойстве, что периоды либо совпадают, либо они попарно не пересекаются, и каждая форма попадет только в один из периодов.
Пример. Все приведенные неопределенные формы с дискриминантом ![]() разбиваются на следующие шесть периодов:
разбиваются на следующие шесть периодов:
I. ![]() ;
;
II. ![]() ;
;
III. ![]() ;
;
IV. ![]() ;
;
V. ![]() ;
;
VI . ![]()
Видим, что в каждом периоде содержится четное число приведенных форм: в периодах I и II по четыре формы, а в остальных периодах по шесть форм.
Особы интерес представляют так называемые обратные и двусторонние формы, показывающие наряду с гауссовой композицией форм глубокий смысл различия собственной и несобственной эквивалентностью целочисленных бинарных квадратичных форм.
Определение 3. Формы ![]() и
и ![]() , и их классы называются обратными: если
, и их классы называются обратными: если ![]() — один из этих классов, то другой класс
— один из этих классов, то другой класс ![]() будет обратным к классу
будет обратным к классу ![]() в смысле композиции классов.
в смысле композиции классов.
Замечание. Так как форма ![]() переводится в форму
переводится в форму ![]() подстановкой
подстановкой ![]() определителя
определителя ![]() , то каждая форма класса
, то каждая форма класса ![]() несобственно эквивалентна каждой форме из обратного класса
несобственно эквивалентна каждой форме из обратного класса ![]() , и обратно, при несобственной эквивалентности двух форм, их классы будут обратными. (При этом еще учитывается, что если форма
, и обратно, при несобственной эквивалентности двух форм, их классы будут обратными. (При этом еще учитывается, что если форма ![]() несобственно эквивалентна
несобственно эквивалентна ![]() , а
, а ![]() собственно эквивалентна
собственно эквивалентна ![]() , то
, то ![]() несобственно эквивалентна
несобственно эквивалентна ![]() ).
).
Определение 4. Класс бинарных квадратичных форм, совпадающий с обратным, называется двусторонним классом.
Из этого определения с учетом сделанного выше замечания получается предложение 5: каждая форма двустороннего класса несобственно эквивалентна самой себе.
Доказательство. Пусть ![]() — двусторонний класс и
— двусторонний класс и ![]() . Покажем, что
. Покажем, что ![]() несобственно эквивалентна самой себе. Обозначим
несобственно эквивалентна самой себе. Обозначим ![]() .
.
Тогда форма ![]() , и пусть
, и пусть ![]() переводится в
переводится в ![]() подстановкой
подстановкой ![]() , и запишем это в следующем виде:
, и запишем это в следующем виде: ![]() . Т. к.
. Т. к. ![]() — двусторонний класс, т.е.
— двусторонний класс, т.е. ![]() , то
, то ![]() . Но так как
. Но так как ![]() , то
, то ![]() и
и ![]() собственно эквивалентны, то найдется подстановка
собственно эквивалентны, то найдется подстановка ![]() определителя
определителя ![]() , что
, что ![]() . Тогда получаем
. Тогда получаем ![]() , т. е.
, т. е. ![]() . Но так как
. Но так как ![]() , то форма
, то форма ![]() несобственно эквивалентна самой себе.
несобственно эквивалентна самой себе.
Предложение 5 доказано.
Определение 5. Форма ![]() , в которой
, в которой ![]() делится на
делится на ![]() , называется двусторонней.
, называется двусторонней.
Следующие два предложения дают некоторую информацию о строении двусторонних классов.
Предложение 6. В каждом двустороннем классе содержится по крайней мере одна двусторонняя форма .
Предложение 7. В каждом двустороннем классе положительного дискриминанта содержатся две и только две приведенные двусторонние формы.
Доказательство этих предложений имеются в [1,2].
Перейдем теперь к изложению основных результатов этого параграфа. Возникает еще вопрос: всегда ли двусторонняя форма принадлежит некоторому двустороннему классу. Ответ дает следующая теорема.
Теорема 1. Каждая двусторонняя форма принадлежит некоторому двустороннему классу.
Доказательство. Пусть ![]() — двусторонняя форма, т.е.
— двусторонняя форма, т.е. ![]() (
( ![]() делится на
делится на ![]() ), и обозначим ее класс через
), и обозначим ее класс через ![]() . Покажем, что
. Покажем, что ![]() — двусторонний класс. По определению, обратная к
— двусторонний класс. По определению, обратная к ![]() форме
форме ![]() . Так как
. Так как ![]() , то форма
, то форма ![]() переводится в себя подстановкой
переводится в себя подстановкой 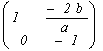 . Далее имеем, что
. Далее имеем, что ![]() переводится в
переводится в ![]() подстановкой
подстановкой
![]()
определителя 1, т.е. ![]() и
и ![]() собственно эквивалентны. Тогда они принадлежат одному и тому же классу, т.е.
собственно эквивалентны. Тогда они принадлежат одному и тому же классу, т.е. ![]() , и значит,
, и значит, ![]() — двусторонний класс
— двусторонний класс
Теорема 1 доказана.
В связи с предложением 7 возникает еще следующий вопрос: могут ли быть в периоде форм двустороннего класса приведенные двусторонние формы соседними друг другу? Следующее утверждение дает необходимое условие того, что двусторонние приведенные формы будут соседними.
Теорема 2. Для того чтобы двусторонние примитивные приведенные формы ![]() и
и ![]() из двустороннего класса дискриминанта
из двустороннего класса дискриминанта ![]() были соседними необходимо, чтобы
были соседними необходимо, чтобы ![]() , где
, где ![]() — целая часть числа
— целая часть числа ![]() .
.
Доказательство. Пусть формы ![]() и
и ![]() соседние. Тогда
соседние. Тогда ![]() , где
, где ![]() — некоторое целое число. Так как
— некоторое целое число. Так как ![]() и
и ![]() — двусторонние формы, то
— двусторонние формы, то ![]() и
и ![]() , где последнюю делимость можно заменить следующим условием:
, где последнюю делимость можно заменить следующим условием: ![]() или что тоже самое
или что тоже самое ![]() , откуда
, откуда ![]() . Тогда в силу взаимной простоты
. Тогда в силу взаимной простоты ![]() и
и ![]() (это следует из примитивности формы
(это следует из примитивности формы ![]() ) из условий делимости
) из условий делимости ![]() и
и ![]() следует, что
следует, что ![]() . Но так как
. Но так как ![]() , то
, то ![]() или, что то же самое:
или, что то же самое: 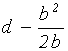 . Из последнего условия делимости следует неравенство
. Из последнего условия делимости следует неравенство ![]() , откуда
, откуда ![]() . Но так как форма
. Но так как форма ![]() приведенная, то для числа
приведенная, то для числа ![]() должны выполняться неравенства
должны выполняться неравенства ![]() , из которых в свою очередь следует, что
, из которых в свою очередь следует, что ![]() .
.
Теорема 2 доказана.
Пример. Для ![]() следующие четыре периода по две соседние двусторонние формы.
следующие четыре периода по две соседние двусторонние формы.
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
При этом эти формы удовлетворяют теореме 2, т.к. ![]() .
.
Замечание. Из полученной теоремы следует, что приведенные двусторонние формы будут соседними в очень малом числе случаев, и в большинстве случаев они не будут соседними. Вопрос о точном числе случаев, когда приведенные двусторонние формы будут соседними, по-видимому, является очень трудным, и мы его не рассматриваем.
Об оценке сверху числа приведенных неопределенных бинарных квадратичных форм
О числе приведенных неопределенных бинарных квадратичных форм, так и о числе классов неопределенных квадратичных форм, известно очень мало. Для числа классов бинарных квадратичных форм имеется точная формула Дирихле. Другим важным результатом являются неравенства, принадлежащие немецкому математику Зигелю.
![]() ,
,
где ![]() — число приведенных неопределенных бинарных квадратичных форм дискриминанта
— число приведенных неопределенных бинарных квадратичных форм дискриминанта ![]() ;
; ![]() и
и ![]() — положительные постоянные, зависящие от
— положительные постоянные, зависящие от ![]() ; причем
; причем ![]() — любое фиксированное положительное число. Наша цель состоит в том, чтобы элементарным способом доказать верхнюю оценку в неравенствах Зигеля для
— любое фиксированное положительное число. Наша цель состоит в том, чтобы элементарным способом доказать верхнюю оценку в неравенствах Зигеля для ![]() . Приводимое доказательство будет опираться на некоторые свойства функции числа положительных делителей натурального числа, и мы их приведем вначале.
. Приводимое доказательство будет опираться на некоторые свойства функции числа положительных делителей натурального числа, и мы их приведем вначале.
Арифметическая функция ![]() определяется как число положительных делителей натурального числа
определяется как число положительных делителей натурального числа ![]() .
.
Предложение 1. Функция ![]() мультипликативна, т.е.
мультипликативна, т.е. ![]() , если
, если ![]() .
.
Из этого предложения 1 легко выводится следующее.
Предложение 2. Если ![]() — каноническое разложение натурального числа
— каноническое разложение натурального числа ![]() , то
, то
![]()
Доказательства предложений 1 и 2 приводятся во всех учебниках по теории чисел (напр. см. [4,6]).
Предложение 3. Для числа ![]() делителя натурального числа имеет место неравенство
делителя натурального числа имеет место неравенство
![]()
Доказательство. Пусть ![]() и
и ![]() — канонические разложения чисел
— канонические разложения чисел ![]() и
и ![]() , и пусть
, и пусть
![]() ,
, ![]() ,…,
,…, ![]() — все простые делители наибольшего общего делителя чисел
— все простые делители наибольшего общего делителя чисел ![]() и
и ![]() . Тогда ясно, что
. Тогда ясно, что
![]()
![]() . (1)
. (1)
Но так как справедливо неравенство
![]()
![]() , (2)
, (2)
то неравенство (1) с учетом (2) и предложения 2 перейдет в следующие соотношения:
![]()
![]()
![]()
Предложение 3 доказано.
Предложение 4. Для ![]() имеет место неравенство
имеет место неравенство
![]() ,
,
где ![]() —произвольное положительное число,
—произвольное положительное число, ![]() —постоянная, зависящая только от
—постоянная, зависящая только от ![]() .
.
Доказательство. Мы следуем рассуждениям в [4,5] (доказательство имеется также в [3]). Пусть ![]() — каноническое разложение числа
— каноническое разложение числа ![]() . Тогда имеем:
. Тогда имеем:
![]()
Рассмотрим отношение 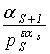 , в случаях
, в случаях ![]() и
и ![]() .
.
Если ![]() , то
, то 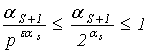 , так как
, так как ![]() .
.
Если ![]() , то считая
, то считая ![]() , получим:
, получим:
![]()
Поэтому 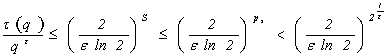
Следовательно, полагая 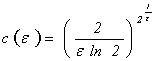 , получим неравенство
, получим неравенство
![]()
Предложение 4 доказано.
Следующее предложение характеризует среднее значение ![]() в нужной для нас форме
в нужной для нас форме
Предложение 5. Для ![]() имеет место следующая оценка сверху:
имеет место следующая оценка сверху:
![]() ,
,
где ![]() — постоянная
— постоянная ![]()
Доказательство. Имеем:
![]()
Последняя сумма геометрически представляет собой число целых точек в первой четверти, лежащих на или под гиперболой ![]() , при этом целые точки, лежащие на осях координат, исключаются, так как для них
, при этом целые точки, лежащие на осях координат, исключаются, так как для них ![]() . Поэтому исследуемую сумму можно записать в виде:
. Поэтому исследуемую сумму можно записать в виде:
![]() , где
, где ![]() — целая часть числа
— целая часть числа ![]()
Оцениваем теперь сумму:
![]() ,
,
где ![]()
Здесь мы воспользовались следующим соотношением из математического анализа
![]() ,
,
где
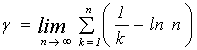 —
—
есть так называемая постоянная Эйлера.
Предложение 5 доказано.
Перейдем теперь к элементарному доказательству следующего результата.
Теорема (Зигель). Для числа ![]() всех приведенных неопределенных бинарных квадратичных форм дискриминанта
всех приведенных неопределенных бинарных квадратичных форм дискриминанта ![]() справедливо неравенство
справедливо неравенство
![]() ,
,
где ![]() — произвольное положительное число,
— произвольное положительное число, ![]() — постоянная, зависящая только от
— постоянная, зависящая только от ![]() .
.
Доказательство. Пусть ![]() — неопределенная приведенная форма дискриминанта
— неопределенная приведенная форма дискриминанта ![]() . Тогда
. Тогда ![]() ,
,
![]() ,
, ![]()
Оценим сверху число приведенных форм с ![]() и
и ![]() . Тогда
. Тогда
![]()
Применяя к последней сумме предложения 3,4,5, получим:
![]()
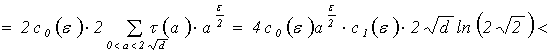
![]()
![]()
![]()
![]() , где
, где ![]()
Теорема доказана.
О диагональных формах и оценка снизу числа классов в роде
В этом параграфе мы получим одну оценку снизу для числа классов в роде неопределенных бинарных квадратичных форм. Сначала введем соответствующие понятия.
Определение 1. Целое число ![]() , не делящееся на простое число
, не делящееся на простое число ![]() , называется квадратичным вычетом по модулю простого числа, если число
, называется квадратичным вычетом по модулю простого числа, если число ![]() сравнимо с квадратом некоторого целого числа по модулю
сравнимо с квадратом некоторого целого числа по модулю ![]() , т.е.
, т.е. ![]() — квадратичный вычет по модулю
— квадратичный вычет по модулю ![]() , если сравнение
, если сравнение ![]() имеет решение; в противном случае число
имеет решение; в противном случае число ![]() называется квадратичным невычетом по модулю
называется квадратичным невычетом по модулю ![]() . В теории квадратичных вычетов очень полезно использование так называемого символа Лежандра.
. В теории квадратичных вычетов очень полезно использование так называемого символа Лежандра.
Определение 2. Символом Лежандра ![]() числа
числа ![]() по простому модулю
по простому модулю ![]() , которое определяется следующим соотношением:
, которое определяется следующим соотношением:

Приведем некоторые основные свойства символа Лежандра, которые нам понадобятся.
Свойство 1 . 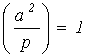 , если
, если ![]()
Свойство 2 . Если ![]() , то
, то ![]() (свойство периодичности)
(свойство периодичности)
Свойство 3 . 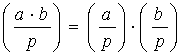 (свойство мультипликативности)
(свойство мультипликативности)
Свойство 4 . ![]() , если
, если ![]()
Определим теперь понятие рода квадратичных форм, впервые введенное Гауссом. Совокупность классов собственно примитивного порядка данного дискриминанта ![]() Гаусс в своей арифметической теории квадратичных форм разделяет на ряды, относя в один и тот же род все те классы, формы которых имеют и тот же «характер». Под характером примитивной формы или примитивного класса форм Гаусс понимает следующее.
Гаусс в своей арифметической теории квадратичных форм разделяет на ряды, относя в один и тот же род все те классы, формы которых имеют и тот же «характер». Под характером примитивной формы или примитивного класса форм Гаусс понимает следующее.
Пусть ![]() — простой делитель дискриминанта
— простой делитель дискриминанта ![]() , и пусть число всех этих различных модулей
, и пусть число всех этих различных модулей ![]() равно
равно ![]() . Можно показать, что если
. Можно показать, что если ![]() — один из этих
— один из этих ![]() модулей, то для всех чисел
модулей, то для всех чисел ![]() , представимых данной собственно примитивной формой дискриминанта
, представимых данной собственно примитивной формой дискриминанта ![]() и взаимно простых с
и взаимно простых с ![]() , символы Лежандра
, символы Лежандра ![]() имеют одно и то же значение. В самом деле, пусть
имеют одно и то же значение. В самом деле, пусть
![]() — собственно примитивная форма дискриминанта
— собственно примитивная форма дискриминанта ![]() и
и ![]() — любой нечетный простой делитель числа
— любой нечетный простой делитель числа ![]() , и
, и ![]() ,
, ![]() — два числа, представляемых формой
— два числа, представляемых формой ![]() и не делящихся на
и не делящихся на ![]() . Подстановка
. Подстановка 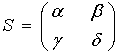 определителя
определителя ![]() переводит
переводит ![]() в форму
в форму ![]() (см. соотношения (3) §1), причем
(см. соотношения (3) §1), причем ![]() , откуда
, откуда ![]() , т.е. в силу определения символа Лежандра имеем
, т.е. в силу определения символа Лежандра имеем ![]() . Из этого равенства в очередь на основании свойств 3 и 4следует, что
. Из этого равенства в очередь на основании свойств 3 и 4следует, что ![]() .
.
Символ Лежандра ![]() имеет одно и то же значение для всех чисел
имеет одно и то же значение для всех чисел ![]() , представляемых формой
, представляемых формой ![]() . Выпишем эти символы Лежандра, которые все равны
. Выпишем эти символы Лежандра, которые все равны ![]() или
или ![]() для всех
для всех ![]() указанных модулей
указанных модулей ![]() , взятых в определенном выбранном порядке.
, взятых в определенном выбранном порядке.
Тогда для данной квадратичной формы получается некоторая определенная последовательность ![]() чисел, равных
чисел, равных ![]() . Эта последовательность чисел, равных
. Эта последовательность чисел, равных ![]() , и называется характером рассматриваемой собственно примитивной бинарной квадратичной формы дискриминанта
, и называется характером рассматриваемой собственно примитивной бинарной квадратичной формы дискриминанта ![]() или характером класса этой формы.
или характером класса этой формы.
Так как число всех различных последовательностей, составленных из ![]() членов, равных
членов, равных ![]() или
или ![]() равно
равно ![]() , то число различных характеров форм данного дискриминанта, а следовательно, и число родов не больше, чем
, то число различных характеров форм данного дискриминанта, а следовательно, и число родов не больше, чем ![]() . Чтобы решить вопрос о точном числе родов, Гаусс вводит в рассмотрение операции композиции классов и композиции родов квадратичных форм.
. Чтобы решить вопрос о точном числе родов, Гаусс вводит в рассмотрение операции композиции классов и композиции родов квадратичных форм.
Не вдаваясь в эту сложную теорию Гаусса, мы приведем его результаты о числе родов и о числе классов в каждом роде.
Каждый род собственно примитивного порядка содержит одно и то же число классов,
![]() , где
, где ![]() — число родов,
— число родов, ![]() — число всех классов,
— число всех классов, ![]() — число классов в каждом роде.
— число классов в каждом роде.
Если для каждого квадратного делителя ![]() дискриминанта
дискриминанта ![]() выполнены условия:
выполнены условия:
НОД ![]() ,
, 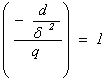
![]() простого
простого ![]() ,
,
то для числа ![]() классов неопределенных квадратичных форм дискриминанта
классов неопределенных квадратичных форм дискриминанта ![]() в каждом роде собственно примитивного порядка выполняется неравенство
в каждом роде собственно примитивного порядка выполняется неравенство
![]()
Примем ![]() за собственно примитивную форму дискриминанта
за собственно примитивную форму дискриминанта ![]() .
.
НОД ![]() .Она является целым числом
.Она является целым числом ![]() , т.е.
, т.е. ![]() при некоторых целых
при некоторых целых ![]() и
и ![]() .
. ![]() , где
, где ![]() — целое число. Значит, символ Лежандра числа
— целое число. Значит, символ Лежандра числа ![]() равен
равен
![]()
При любом ![]() получаем
получаем 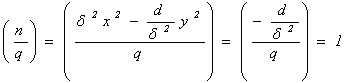
Это говорит о том, что форма ![]() принадлежит главному роду. Число форма приравнивается числу квадратных делителей
принадлежит главному роду. Число форма приравнивается числу квадратных делителей ![]() дискриминанта
дискриминанта ![]() с условием НОД
с условием НОД ![]()
Тогда получаем:
![]() с условием
с условием 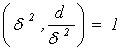
Такая оценка справедлива также для числа классов всех остальных родов
![]() — диагональная форма дискриминанта
— диагональная форма дискриминанта ![]() . Эта форма не эквивалентна никакой другой диагональной форме того же дискриминанта.
. Эта форма не эквивалентна никакой другой диагональной форме того же дискриминанта.
Предположим, что
![]() (1)
(1)
дискриминанта ![]() собственно эквивалентна другой диагональной форме.
собственно эквивалентна другой диагональной форме.
![]() (2)
(2)
того же дискриминанта ![]() .
.
Определим целочисленную унимодулярную подстановку ![]() .
.
Эта подстановка заменяет форму ![]() в форму
в форму ![]() .
.
Получаем:
![]() , (3)
, (3)
где
![]() (4)
(4)
Преобразуя данные выражения находим
![]()
![]()
Однако необходимо форму ![]()
![]() (5) привести к диагональной. Для это перепишем форму
(5) привести к диагональной. Для это перепишем форму ![]() :
:
![]() . (6)
. (6)
В связи с тем, что ![]() имеет тот же дискриминант, что и
имеет тот же дискриминант, что и ![]() получим:
получим:
![]() , (7)
, (7)
и аналогично
![]() ;
;
![]() ;
;
![]() (8)
(8)
Принимая во внимание условие, указанное выше форма (8) будет иметь вид:
![]() , что противоречит условию (4).
, что противоречит условию (4).
Число родов бинарных квадратичных форм в данном собственно примитивном порядке дискриминанта ![]() равно
равно ![]() , где
, где ![]() определяется следующими условиями:
определяется следующими условиями:
![]() при
при ![]() ,
,
![]() при
при ![]() ,
,
![]() при
при ![]() ,
,
при этом ![]() — число различных простых делителей числа
— число различных простых делителей числа ![]() .
.
Данное высказывание используется в оценке снизу числа классов в роде неопределенных бинарных квадратичных форм собственно примитивного порядка.
Список литературыБухштаб А. А. Теория чисел. М., 1966.
Гаусс К. Ф. Труды по теории чисел. Изд-во АН СССР, М., 1959.
Венков Б. А. Элементарная теория чисел. М-Л., 1937.
Виноградов И. М. Метод тригонометрических сумм в теории чисел. М., «Наука», 1980.
Чандрасекхаран К. Введение в аналитическую теорию чисел. М., Мир. 1974.
Виноградов И. М. Основы теории чисел. М., Наука. 1972 с.
Похожие работы
... постоянная Эйлера. Предложение 5 доказано. Перейдем теперь к элементарному доказательству следующего результата. Теорема (Зигель). Для числа всех приведенных неопределенных бинарных квадратичных форм дискриминанта справедливо неравенство , где - произвольное положительное число, - постоянная, зависящая только от . Доказательство. Пусть - неопределенная ...
... , что этот факт может быть использован для конструирования дискретных схем, решающих задачу математического программирования на аппаратном уровне. 2. Аналоговые логические элементы Описываемые ниже электрические цепи содержат источники напряжения, резисторы, диоды и трансформаторы постоянного тока. Все эти элементы рассмотрены Деннисом [1] в аналогичном контексте и мы будем пользоваться его ...
... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...
... однороден, можно считать, что цвет изображения несет информацию о свойствах поверхности объекта, о ее форме, а яркость в значительной степени зависит и от условий “освещения”. Поэтому на практике в задачах морфологического анализа цветных изображений сцен важное значение имеет понятие формы изображения, имеющего постоянный цвет и произвольное распределение яркости в пределах заданных подмножеств ...
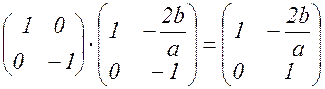
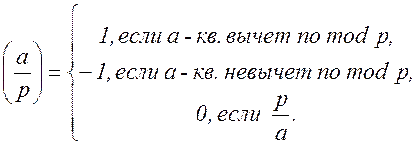
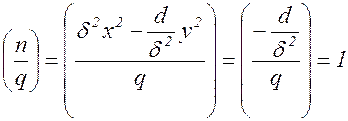

0 комментариев