Навигация
При вычислении расстояния от точки до конуса воспользуемся следующим результатом из [5]
1.6. При вычислении расстояния от точки до конуса воспользуемся следующим результатом из [5].
Пусть (Е, Е+) Î (Â) и х Î Е+. Элемент x+ Î Е+ является ближайшим к х элементом конуса Е+ тогда и только тогда, когда существует f Î Е*+, ||f|| = 1, такой, что f(x+) = 0, f(x-) = ||x-||. В этом случае d(x, Е+) = ||x-||.
1.7. Пусть E – банахово пространство над R со строго регулярным замкнутым конусом Е+. Элементы x, у Î Е+ называются н-дизъюнктными или ортогональными по Роберу (обозначается x ![]() у), если ||x + λу|| = ||x – λу|| для любого λ ≥ 0.
у), если ||x + λу|| = ||x – λу|| для любого λ ≥ 0.
2. Описание множеств |Х|, Х+, Х-
Рассмотрим пространство ![]() , упорядоченное регулярным круглым конусом K(f,a), где a = 0,5 и функционал f имеет первую координату, равную единице, а остальные координаты нулевые:
, упорядоченное регулярным круглым конусом K(f,a), где a = 0,5 и функционал f имеет первую координату, равную единице, а остальные координаты нулевые:
K1 = {x = (x1, x2, ..., xn) : x1 ≥ |x2| + … + |xn|}.
Все результаты легко перенести на общий случай (1) с помощью изометричного преобразования. В дальнейшем, если не указано иное, будем обозначать через X = ![]() .
.
Опишем множества |Х|, Х+, Х- для произвольного элемента x = (x1, ..., xn) Î ![]() . Заметим, что частный случай разложения элемента х на ортогональные по Роберу положительную и отрицательную части рассмотрен в [6].
. Заметим, что частный случай разложения элемента х на ортогональные по Роберу положительную и отрицательную части рассмотрен в [6].
2.1. Пусть x1 = 0. Найдем элемент конуса, который мажорирует элементы ± х и равен им по норме, т. е. у = (у1, …, yn) : y1 ≥ ![]() , y ≥ ± х, ||y|| = ||x||. Такой элемент описывает следующая система:
, y ≥ ± х, ||y|| = ||x||. Такой элемент описывает следующая система:
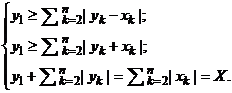
Сложив первые два неравенства, получим оценку у1 ≥ X. С другой стороны, из третьего равенства видно, что у1 ≤ X. Тогда у1 = X, ![]() = 0, следовательно yk = 0 для любого
= 0, следовательно yk = 0 для любого ![]() . Получаем следующее представление метрического модуля элемента х и его положительной и отрицательной части
. Получаем следующее представление метрического модуля элемента х и его положительной и отрицательной части
![]() ,
,
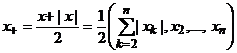 ,
,
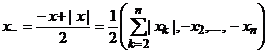 .
.
2.2. Пусть x1 > 0. В этом случае система, описывающая элемент у Î |Х|, имеет вид:
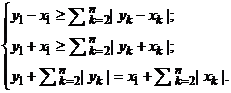
Аналогичные действия позволяют утверждать, что X≤у1≤X + х1, т.е. у1 представим в виде у1 = X + λх1, где 0 ≤ λ ≤ 1. Последовательно подставляя значение у1 в систему, имеем: ![]() -|yk – xk|) ≥ ≥ х1(l – λ) =
-|yk – xk|) ≥ ≥ х1(l – λ) = ![]() , с другой стороны, |уk| = |xk + (yk – xk)| ≥ ≥ |xk| – |yk – xk|. В итоге получаем:
, с другой стороны, |уk| = |xk + (yk – xk)| ≥ ≥ |xk| – |yk – xk|. В итоге получаем:
|xk| = |yk| + |yk − xk| (![]() ).
).
Из этого равенства следует, что уk и хk – yk – одного знака, что приводит к следующим выводам:
если (xk − yk) > 0 и yk > 0, то 0 < yk < xk ;
если (xk − yk) < 0 и yk < 0, то xk < yk < 0;
если (хк – yk) = 0 и yk = 0, то хk = уk = 0.
Из чего следует, что каждая координата уk (![]() ) представима в виде уk = λkхk, 0 ≤ λk ≤ 1.
) представима в виде уk = λkхk, 0 ≤ λk ≤ 1.
Отметим равенство, используемое в дальнейшем:
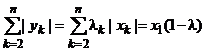 .
.
Итак, при x1 > 0 имеем:
![]()
где 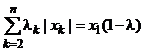 , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
![]()
где 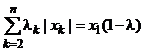 , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
![]()
где 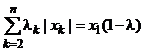 , 0 ≤ λ, λk ≤ 1}.
, 0 ≤ λ, λk ≤ 1}.
2.3. Пусть x1 < 0. Система, описывающая элемент у Î |Х|, на этот раз имеет вид:
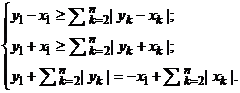
Выполнив аналогичные пункту 2.2 действия, получим X ≤ у1 ≤ X – х1. В этом случае y1 = Х + λ|x1|, где 0 ≤ λ ≤ 1. Подставляя последовательно значение у1 в систему, получаем
![]()
![]() и
и ![]() .
.
Откуда выводим:
|xk| = |yk| + |yk + xk| (![]() ).
).
Отсюда следует, что – yk и (xk + yk) – одного знака. Вновь получаем, что уk = –λkxk , 0≤λk≤1. При этом ![]() =
=![]() =
= ![]() .
.
Итак, при х1 < 0 имеем:
![]()
где 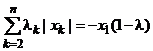 , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
![]()
где 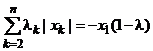 , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
![]()
где 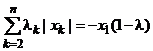 , 0 ≤ λ, λk ≤ 1}.
, 0 ≤ λ, λk ≤ 1}.
2.4. Общий случай. Для произвольного элемента х = (x1, ..., xn) и круглого регулярного конуса Kj (1) имеем:
![]()
где 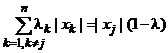 , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
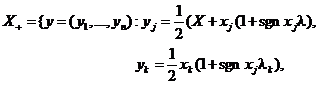
где 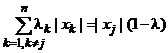 , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
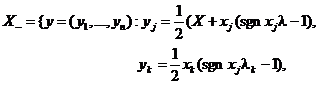
где 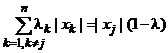 , 0 ≤ λ, λk ≤ 1};
, 0 ≤ λ, λk ≤ 1};
| 2 Труды молодых ученых, 2005 (1) |
3. Нахождение расстояния от элемента до конуса
Пусть элемент x принадлежит конусу К1, т.е. х1 ≥ X. В этом случае d(x, K1) = 0, а ближайшим элементом конуса является он сам.
Пусть элемент х принадлежит конусу – К1, т.е. -х1 ≥ X. В этом случае очевидно d(x, K1) = ||х||, а ближайшим элементом конуса является ноль.
Пусть х1 = 0 и элемент х не принадлежит конусу ±К1. Покажем, что d(x, K1) = ||х–||, а ближайшим элементом конуса является х+. Согласно следствию 2.2.13 [5], для этого необходимо найти функционал f Î К*1 такой, что ||f|| = 1, f(x+) = 0, f(x-) = ||x-||,
где x+ – x- = x, ||x+ + x-|| = ||x||.
В качестве такого функционала выберем f=(1, –sgn x2, ...,–sgn xn). Для любого элемента конуса аÎК1 справедливо f(а)=a1 –![]() , т. е. f положительный функционал. Очевидно, что его норма равна единице. Элементы x+ и x–, вычисляемые по формулам 2.1, удовлетворяют условиям следствия 2.2.14 [5]. Кроме того,
, т. е. f положительный функционал. Очевидно, что его норма равна единице. Элементы x+ и x–, вычисляемые по формулам 2.1, удовлетворяют условиям следствия 2.2.14 [5]. Кроме того,
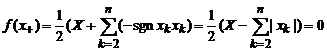 ,
,
![]() .
.
Учитывая, что ||x–|| = ![]() || (Х, x2, ... , хn)|| = X, имеем, что f(x-) = =||x-||. Таким образом, условия следствия 2.2.14 [5] выполняются полностью, и мы приходим к выводу, что
|| (Х, x2, ... , хn)|| = X, имеем, что f(x-) = =||x-||. Таким образом, условия следствия 2.2.14 [5] выполняются полностью, и мы приходим к выводу, что
d(x, K1) = || x-|| = ![]() =X, а x+ является ближайшим к х элементом конуса.
=X, а x+ является ближайшим к х элементом конуса.
3.4. Пусть X > х1 > 0. Положив λ = 0 в формулах 2.2, получим:
![]()
![]() ) .
) .
В этом случае очевидно, что x+ – x- = x, || x+ + x-|| = ||x||.
Рассматривая функционал из 3.3, находим:
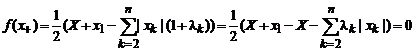 ,
,
![]() .
.
Заметим, что в этих рассуждениях использован результат, полученный в 2.2, о том, что ![]() .
.
В итоге получаем, что d(x, K1) = ||x-|| = ![]() , a x+ является ближайшим к x элементом конуса.
, a x+ является ближайшим к x элементом конуса.
Похожие работы
... пространственно-временным миром. Найденное Эйнштейном объединение принципа относительности Галилея с относительностью одновременности получило название принципа относительности Эйнштейна. Понятие относительности стало одним из основных понятий в современном естествознании. 1.4 Общая теория относительности о пространстве и времени Был этот мир глубокой тьмой окутан. Да будет свет! И вот ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
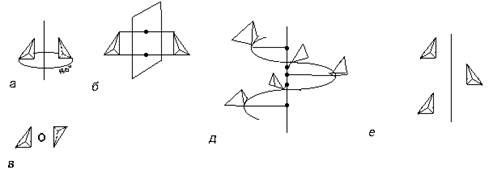
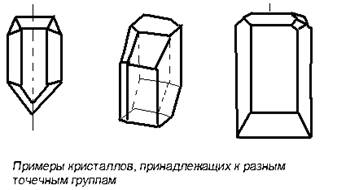
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...
... шланги. Их укладывают под растения так, чтобы вода попадала непосредственно на всю площадь корневой системы. "Зеленые комнаты" и лабиринты Еще один важный принцип планирования регулярных садов- разделение ландшафта на различные по оформлению "зеленые комнаты". Причем высокие живые изгороди позволяют создавать не только обособленные "комнаты", но и целые лабиринты. Кстати, в наше время, когда ...





0 комментариев