Навигация
Пусть х1 < 0 и – х1 > X. Если λ = 0 в формулах 2.3, то элементы
3.5. Пусть х1 < 0 и – х1 > X. Если λ = 0 в формулах 2.3, то элементы
![]()
![]() )
)
удовлетворяют условиям x+ – x- = x и ||x+ + x-|| = ||x||, причем f(x+) = 0, f(x-) = ||x-||, где f – функционал из 3.3.
Таким образом, в этом случае d(x, K1) = ||x-|| = ![]() , a x+ – ближайший к x элемент конуса.
, a x+ – ближайший к x элемент конуса.
Аналогичные рассуждения показывают, что данные результаты справедливы и для конуса Kj.
3.6. Данные рассуждения подтверждают результат утверждения 2.3 из [6] о том, что
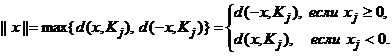
4. Описание множества М(х)
Элемент x принадлежит конусу К1. В этом случае расстояние d(x, K1) = ||x–|| = 0. Если а = (a1, ..., аn) Î М(x), то а Î К1 и ||а – x|| = 0, откуда следует, что а = x и M(x) = {x}.
Элемент х принадлежит конусу –К1. В этом случае x1 ≤ –X и расстояние
d(x, К1) = ||x||. Если a = (a1, ..., аn) Î М(x), то a1 ![]() = A и ||a – x|| = ||x||, что равносильно |а1 – x1| +
= A и ||a – x|| = ||x||, что равносильно |а1 – x1| + ![]() = –x1 + +
= –x1 + +![]() . Откуда следует, что а1 =
. Откуда следует, что а1 =![]() -
- ![]() ≥
≥ ![]() =A.
=A.
Получаем, что ![]() ≥
≥ ![]()
![]() ≥ ≥
≥ ≥ ![]() .
.
Равенство | xk – аk| + |аk| = |xk| для любого ![]() означает, что аk и (xk – аk) – одного знака, т. е. аk = ak xk, где 0 ≤ ak ≤ 1 для любого
означает, что аk и (xk – аk) – одного знака, т. е. аk = ak xk, где 0 ≤ ak ≤ 1 для любого ![]() . Выражение для а1 имеет вид: а1 =
. Выражение для а1 имеет вид: а1 = ![]() .
.
В итоге получаем, что
![]() где 0≤ak≤1,
где 0≤ak≤1,![]() }.
}.
4.3. x1 = 0 и элемент х не принадлежит конусу К1. Пусть а = (a1, ..., an) Î М(x). Из определения М(х) следует, что a1 ≥ А и ||а – x|| = =![]() + |a1| =
+ |a1| = ![]() . Из последних равенств получаем: а1 =
. Из последних равенств получаем: а1 = ![]() –
– ![]() ≥
≥ ![]() или следующую цепочку
или следующую цепочку ![]() ≥
≥ ![]() =
= ![]() + +
+ +![]() ≥
≥ ![]() . Это равносильно
. Это равносильно ![]() + +
+ +![]() =
= ![]() . В итоге вновь получаем равенство
. В итоге вновь получаем равенство
|xk −ak| + |ak| = |xk| (![]() ),
),
которое равносильно утверждению, что
![]() где 0≤ak≤1,
где 0≤ak≤1, ![]() }.
}.
4.4. Пусть x1 > 0 и элемент x не принадлежит конусу K1. Если а = (a1, ..., аn) Î М(x), то ||a – x|| = ||x–|| = d(x, К1) = ![]() – x1
– x1
или 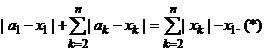
Так как a Î K1 , то а1 ≥ ![]() . Тогда последовательно получаем a1 ≤ |а1 – x1| + x1 =
. Тогда последовательно получаем a1 ≤ |а1 – x1| + x1 = ![]() -
- ![]() ≤
≤ ![]() ≤ a1 , что равносильно системе
≤ a1 , что равносильно системе
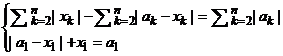
или
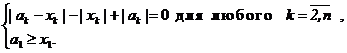
Получаем, что (аk – xk) и xk – одного знака, т. е. аk = akxk, где 0 ≤ ak ≤ 1 для любого ![]() . Подставив в (*), имеем а1 +
. Подставив в (*), имеем а1 + ![]() =
= ![]() .
.
Таким образом, выражение для а1 имеет вид: а1 =![]() .
.
В итоге получаем, что если х1 > 0, то
![]() где 0≤ak≤ 1,
где 0≤ak≤ 1, ![]() }.
}.
4.5. Пусть x1 < 0 и элемент х не принадлежит конусу –К1, т.е. –x1 < ![]() .
.
Если а = (a1, ..., аn) Î М(x), то ||a-x|| = ||x–|| = d(x, К1) =![]() –x1
–x1
или 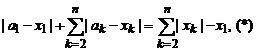
или ![]()
Откуда a1= ![]() -
- ![]() ≥
≥![]() . В то же время
. В то же время ![]() ≥
≥ ![]() +
+ ![]() ≥
≥ ![]() . Из последнего неравенства получаем, что (ak – xk) и (xk) – одного знака для любого k, т. е. аk = ak xk, где 0 ≤ ak ≤ 1 для любого
. Из последнего неравенства получаем, что (ak – xk) и (xk) – одного знака для любого k, т. е. аk = ak xk, где 0 ≤ ak ≤ 1 для любого ![]() . Тогда a1=
. Тогда a1=![]() –
–![]() =
=![]() . Получаем, что (4.4) верно и для этого случая.
. Получаем, что (4.4) верно и для этого случая.
5. Описание множества M(x)∩K1
Интересен вопрос о взаимоотношении множества положительных частей элемента и множества элементов, на которых достигается расстояние от элемента до конуса.
Пусть элемент x принадлежит конусу К1. В этом случае М(х) = {x}, а Х+ = {![]() (Х + x1(1 + λ), x2(1 + λ2), ..., xn(1 + λn)), 0 ≤ λ, λk ≤ 1,
(Х + x1(1 + λ), x2(1 + λ2), ..., xn(1 + λn)), 0 ≤ λ, λk ≤ 1, ![]() = x1(1 – λ)}. При λk = 1 получим λ = 0 и Х+ = {x}, т.е. М(х) ∩ Х+ = {x} и М(х) Ì Х+.
= x1(1 – λ)}. При λk = 1 получим λ = 0 и Х+ = {x}, т.е. М(х) ∩ Х+ = {x} и М(х) Ì Х+.
Пусть элемент x принадлежит конусу –К1. Если аÎ М(x)∩Х+, то, учитывая формулы 4.2 и 2.2, получим:
![]() (
(![]() + x1(1 – λ), x2(1 – λ2), ... , xn(1 – λn)).
+ x1(1 – λ), x2(1 – λ2), ... , xn(1 – λn)).
Из этого равенства следует, что ![]() ) при λk Î[0,1]. Итак, для любого λk,
) при λk Î[0,1]. Итак, для любого λk, ![]() найдется
найдется ![]() такое, что из того, что а Î Х+ следует, что а Î М(х). Обратное не всегда верно. В итоге получаем включение М(x) ∩ Х+ = X+ .
такое, что из того, что а Î Х+ следует, что а Î М(х). Обратное не всегда верно. В итоге получаем включение М(x) ∩ Х+ = X+ .
5.3. Пусть x1 = 0 и элемент x не принадлежит конусу. Воспользовавшись формулами 4.3 и 2.1, получим М(х) ∩ Х+ = Х+.
5.4. Пусть x1 > 0 и элемент x не принадлежит конусу. Если элемент принадлежит М(х) ∩ Х+ , то выполняется равенство:
![]() (
(![]() + x1(1 + λ), x2(1 + λ2), ..., xn(1 + λn)),
+ x1(1 + λ), x2(1 + λ2), ..., xn(1 + λn)),
что равносильно системе
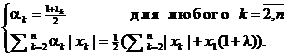
Данные равенства выполняются, если λk такие, что λ = 0. В этом случае ![]() , т.е.
, т.е.
М(x)∩Х+=![]() .
.
5.5. Пусть x1 < 0 и элемент х не принадлежит конусу –К1. Если элемент принадлежит М(х) ∩ Х+ ,то выполняется равенство:
![]() (
(![]() + x1(1 - λ), x2(1 - λ2), ..., xn(1 - λn)),
+ x1(1 - λ), x2(1 - λ2), ..., xn(1 - λn)),
что равносильно системе
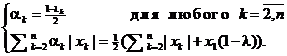
Данные равенства выполняются, если ![]() ], т. е. М(x) ∩ Х+ = М(х).
], т. е. М(x) ∩ Х+ = М(х).
Вулих Б. 3. Введение в теорию конусов в нормированных пространствах. Калинин.: Изд-во КГУ, 1977.
Вулих Б. 3. Специальные вопросы геометрии конусов в нормированных пространствах. Калинин.: Изд-во КГУ, 1978.
Красносельский М. А. Положительные решения операторных уравнений. М.: Физматгиз. 1962.
Вишняков Ю. Г., Худалов В. Т. Описание всех регулярных круглых конусов в ![]() . Вестник СОГУ. Естественные науки. 1999. № 1.
. Вестник СОГУ. Естественные науки. 1999. № 1.
Худалов В. Т. Упорядоченные банаховы пространства и их приложения. Владикавказ: Иристон, 1999.
Коробова К. В. О геометрии регулярных круглых конусов в пространствах ![]() и l1.–Владикавказский мат. журн. 2003. Т. 5,
и l1.–Владикавказский мат. журн. 2003. Т. 5,
Похожие работы
... пространственно-временным миром. Найденное Эйнштейном объединение принципа относительности Галилея с относительностью одновременности получило название принципа относительности Эйнштейна. Понятие относительности стало одним из основных понятий в современном естествознании. 1.4 Общая теория относительности о пространстве и времени Был этот мир глубокой тьмой окутан. Да будет свет! И вот ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
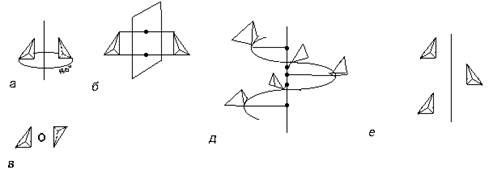
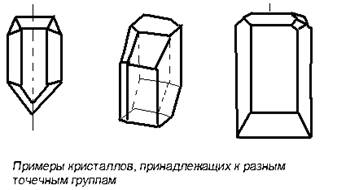
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...
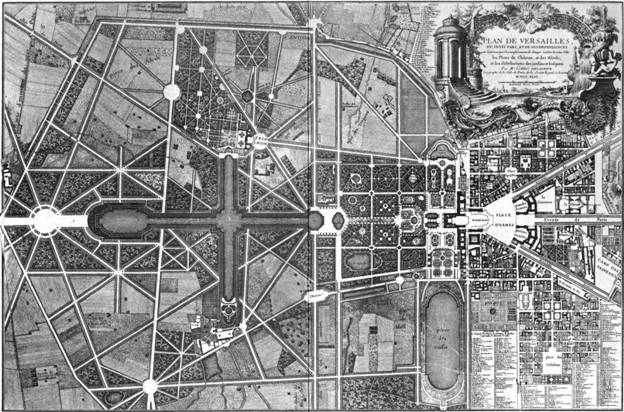
... шланги. Их укладывают под растения так, чтобы вода попадала непосредственно на всю площадь корневой системы. "Зеленые комнаты" и лабиринты Еще один важный принцип планирования регулярных садов- разделение ландшафта на различные по оформлению "зеленые комнаты". Причем высокие живые изгороди позволяют создавать не только обособленные "комнаты", но и целые лабиринты. Кстати, в наше время, когда ...





0 комментариев