A22- a12 a21/ a11…a2n -a1n an1/ a11

0 a22- a12 a21/ a11…a2n -a1n an1/ a11

…………………………………………(5.10)

0 an2- a12 an1/ a11… ann- a1n an1/ a11

Умножим каждую строку в (5.10), начиная со второй на a11,при этом определитель (5.10) умножится на a11n-2

(5.11)

где

a11 a22- a12 a21 a11 a23- a13 a21 … a11 a2n- a1n a21

a11 a32- a12 a31 a11 a33- a13 a31 … a11 a13n- a1n a31

…………………………………………...............……… (5.12)

a11 an2- a12 an1 a11 an3- a13 an1 … a11 ann- a1n an1

Рассмотрим более внимательно элементы (5.12). Перепишем (5.12) в виде

a11 a12 … a1n-1

a21 a22 … a2n-1

…………… ......…… (5.13)

an-11 an-12… an-1n-1

Из сравнения (5.12) и(5.13) видно, что

a11 – есть свертка определителя a11 a12

a21 a22

a12 – есть свертка определителя a11 a13

a21 a23

…………………………………………………..

a1n-1 – есть свертка определителя a11 a1n

a21 a2n

Таким образом, первая строка 1n-1 является сверткой элементов первых двух строк определителя n. Более наглядно это можно сфрмклировать так : последовательно каждый “прямоугольник” элементов первой и второй строк заменяется его сверткой ; причем первые элементы двух строк “участвуют” во всех прямоугольниках этих строк.

a11 a12 a13… a1n

a11 a12 a1n-1

a21 a22 a23… a2n

Аналогично вторая строка определителя n-1 является сверткой элементов первой и третьей строк исходного определителя.

a11 a12 a13… a1n

a21 a22 a2n-1

a31 a32 a33… a3n

Наконец для последней строки n-1 имеем

a11 a12 a13… a1n

an-1 1 an-1 2 an-1n-1

an1 an2 an3… ann

Если теперь применить те же опервции к определителю n-1, т. е. к (5.13), получим

(5.14)

где

a11 a12 … a1 n-2

a21 a22 … a2 n-2

……………………………..

an-2 1 an-2 2… an-2 n-2

а элементы aik являются сверткой соответствующих определителей – прямоугольников.

Очевидно, повторяя эту операцию n–1 раз, получим следующую формулу, предварительно введя более простые обозначения :

a11 = a1– левый угловой верхний элемент

a11 = a2 – левый угловой верхний элемент

a11 = a3 – левый угловой верхний элемент

…………………………………………

a11 = an – левый угловой верхний элемент.

С учетом этого

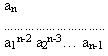(5.15) n>2

Пример №1.

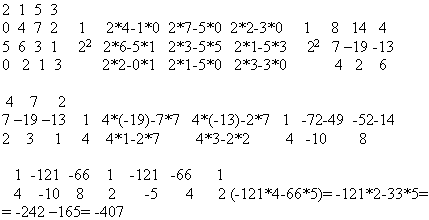
Пример №2.

Вычесленные в порядке получения определителий n, n-1, …, 2 их верхние левые угловые элементы a1,a2,…,an являются критерием Сильвестера в части знаков, т.е.

sign a11=sign a1

sign a11=sign a2=sign a11 a12

a21 a22

………

a11… a1n

sign a11=sign an=sign

………..

an1… ann

По сути метод дает возможность вычисления определителей . Однако нас интересуют лишь знаки определителей.Это существенно упрощает задачу.

Рассмотрим функцию f(x1,x2,…,xn). имеющую экстремум,а именно максимум в точке М0(x10,x20,…,xn0).Это значит,что все коэффициенты a1, a2,…, an должны быть положительными. Поэтому процесс определения максимума функции в точке М0 заканчивается на любом этапе понижения определителя ,если после положительных a1, a2,…, ak коэффициент аk+1 стал отрицательным или нулевым.

Если же в точке М0 – минимум, то коффициенты a1, a2,…, an образуют знакочередующуюся последоватнльность, а именно

a1<0, a2>0, a3<0,…

Аналогично процесс прекращается, если нарушается эта знакопеременность.

Итак, общая схема выглядит следующим образом :

1.Определяются стационарные точки функции, в которых

2.Определяются коэффициенты аik в этих точках

2f xi xr

3.Выясняем знак первого диагонального элемента а11=а1

а) если а11>0, то все последующие элементы а2,а3,…,аn должны быть положительными,если в точке М0 действительно максимум

б)если а11<0, то знаки последующих элементов а2,а3,…,аn должны чередоваться, если в точке М0 действительно минимум.

4.При нарушении какой-либо из закономерностей в п.3 процесс прекращается и формулируется вывод о том,что в точке М0 экстремума нет.

Наконец отметим следующее важное обстоятельство. Так как коэффициенты аik являются частными производными второго порядка и для дифференцируемой функции с непрерывными 2f/ xi xr в соответствии с теоремой Шварца эти частные производные не зависят от порядка дифференцирования, то аik= аki. Это важное свойство приводит к тому, что матрица (аik) является симметрической вместе со своим определителем аik Покажем, что учет этого факта сокращант объем вычислений по крайней мере вдвое .

Во-первых, покажем, что определитель n-1 также остается симметрическим,т. е. применяется операция понижения порядка инварианта и сохраняет это свойство при переходе от n-1 к n и т.д.

Диагональные элементы любого определителя, очевидно, равны сами себе.

Рассмотрим произвольный элемент аik в определителе n-1, i=k, i,k=1,2,…,n-1.

аik= аik – а1 k а1i / а11 (*)

Если переставить индексы i,k ,то

aki= аki – а1 i а1k / а11 (**)

Сравнивая (*) и (**) видим, что из того, что аik= аki следует, что аik= аki. Этим доказано, что из того, что n- симметрический определитель, определитель n-1 также симметрический.Что это дает для вычисления n-1 ?

Пусть вычислена первая строка коэффициентов а1k (k=1,2,…,n-1) определителя n-1 , т.е.

а11, а12, а13,…, а1n-1

Теперь вычислим первый столбец , он имеет вид

а11

а21

а31

…..

аn-1 1

Но ввиду симметричности коэффициентов, этот столбец совпадает со строкой. Другими словами, сосчитав элементы первой строки, первый столбец уже считать нет необходимости, его нужно просто записать. Для наглядности запишем

a11 a12 … a1 n-1

a21 a22… a2 n-1

………………….

an1 an2… an-1 n-1

Вычислим теперь элементы второй строки, начиная с а22 ,т.е. а22, а23, а24,…, а2 n-1.Эта строка полностью совпадает со вторым столбцом, начиная с а22,т.е.

а22

а31

…..

аn-1 2

Итак, второй столбец автоматически заполняется элементами второй строки.Т.е. иммем

a11 a12 а13 … a1 n-1

a21 a22 а23 … a2 n-1

n-1= a31 a32 а33 … a3 n-1

…………………………..

an-1 1 an-1 2 an-1 3 … an-1 n-1

И т.д.

Общий вывод : необходимо расчитать лишь правую треугольную часть элементов. Нижняя же левая часть определителя заполняется автоматически. Формально ее можно вообще не заполнять, т.е. оставлять в виде

a11 a12 а13 … a1 n-1

a22 а23 … a2 n-1

n-1= а33 … a3 n-1 (5.16)

…………..

an-1 n-1

Отсюда для получения следующегоопределителя можно применить правило, условно назовем, треугольника.

a11= a11 a22- a122

a22= a11 a33- a132 и т.д.

Для недиагоналных элементов схема несколько сложнее

a12= a11 a23- a13 a12 a11 a12 а13

а23 и т.д.

Пример №3.

Исследовать на экстремум функцию z=x3+y3-3xy

1.Находим

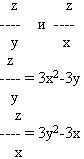
2.Находим стационарные точки, решая систему

3x2-3y=0

3y2-3x=0

Получили две стационарные точкм (0;0) и (1;1).

3.Находим

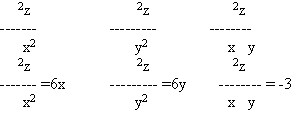
4.Для точки (0;0) имеем

a11=0 a22=0 a12= a21= -3

Для точки (1;1) иммем

b11=6 b22=6 a12= a21= -3

5.Находим

a11 a12 0 -3

a21 a22 -3 0

b11 b12 6 -3

b21 b22 -3 6

Так как <0 , то в точке (0;0) экстремума нет.

Так как >0 и a11>0, то (1;1) – точка минимма функции, причем zmin = -1.

Пример №4.

Исследовать на экстремум функцию w=x2/3+y2/3+z2/3

Ищем критические точки

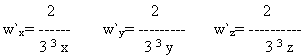
Эти частные производные не обращаются в нуль ни при каких значениях x, y, z; они не сужествуют (обращаются в бесконечность) в точке P0(0;0;0). Точка P0 лежит внутри области определения функции w, которая представляет совокупность всех точек (x;y;z) пространства. Поэтому P0 критическая точка.

Исследуя знак разности w(P)-w(P0)= x2/3+y2/3+z2/3 вблизи точки P0, убеждаемся, что при любых отличных от нуля значениях x,y,z она сохраняет положительный знак. Поэтому P0 есть точка минимума, wmin=w(P0)=0

5.4.Экстремумы на множествах.

Следует обратить внимание на то, что мы указали необходимые и достаточные условия экстремума функции лишь во внутренней точке области определения. Таким образом, при отыскании абсолютного максимума или минимума функции необходимо наряду с внутренними критическими точками функции исследовать также точки границы области определения, поскрльку максимальное или минимальное значение функция может принять в одной из таких граничных точек.

Пусть функция f дифференцируема на открытом ограниченом G и непрерывна на его замыкании G. Пусть требуется найти наибольшее и наименьшее значения функции на множестве G. Для этого можно, например, найти все стационарные точки функции f в G, вычислить в них значения функции и выбрать, если, конечно это возможно (а теоретически возможно это, например, когда число стационарных точек конечно), точки, в которых функция принимает наибольшее и наименьшее значения из всех значений в стационарных точках. После этого следует сравнивать эти значения со значениями, которые функция принимает на границе открытого множества G, например, найдя, если это удается сделать, наибольшее и наименьшее значения функции f на границе области G. Сравнив наибольшее и наименьшее значения в стационарных точках с наибольшим и наименьшим значениями на границе множества G, мы можем, очевидно, найти искомый максимум и минимум f на G.

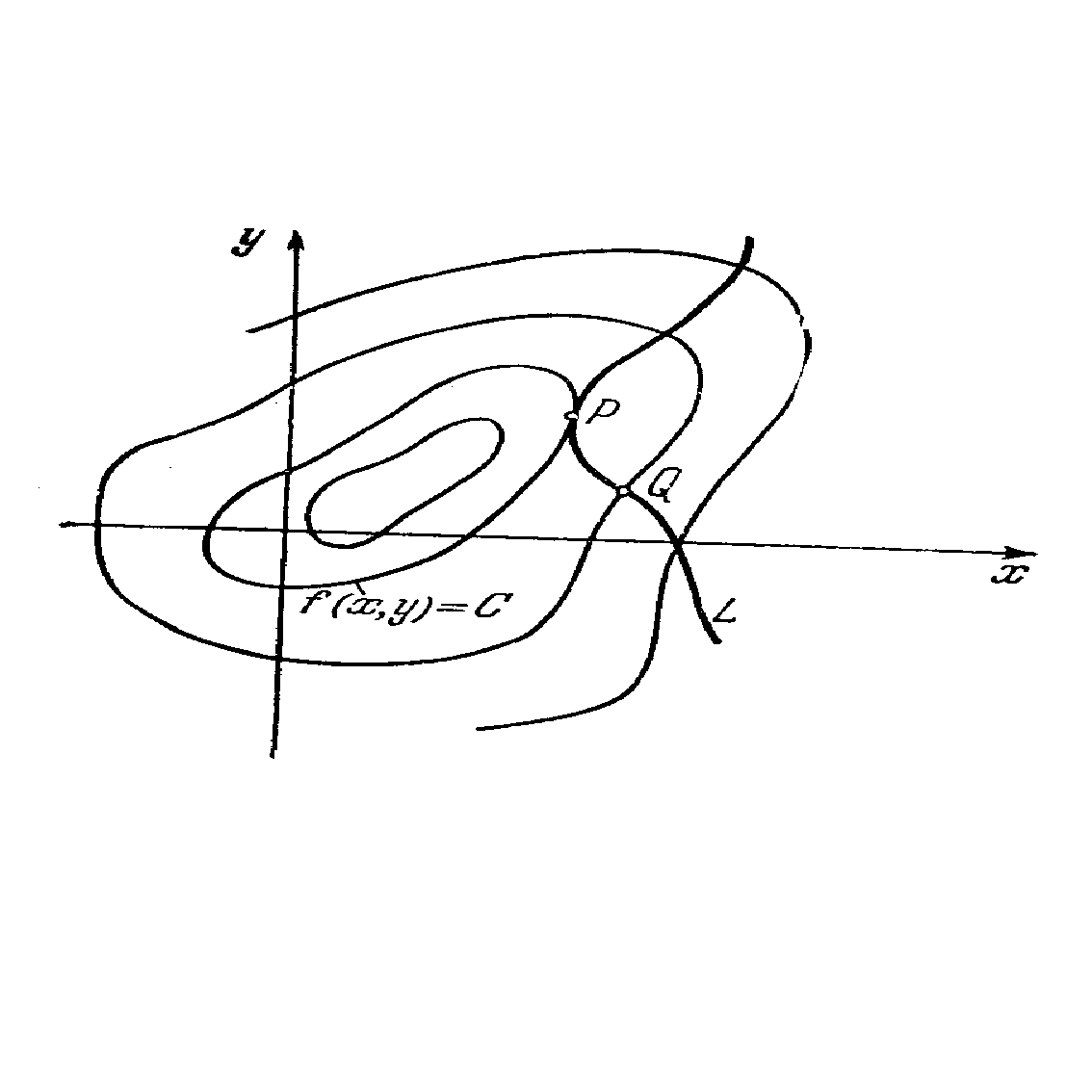
В случае, когда G – плоская область и ее граница является кривой, заданной некоторым представлением x=x(t), y=y(t), <t< вопрос о нахождении экстремальных значений функции f(x,y) на границе G сводится к исследованию на экстремум функции одного переменного f(x(t),y(t)), что делается уже известными нами методами.

Методы, которые можно применять в многомерном случае для отыскания экстремальных точек на границе области будут рассмотрены позже (см. раздел, посвященный условному экстремуму).

Полезно лишь иметь ввиду, что при отыскании максимумов и минимумов часто наряду с формальной техникой, а иногда и вместо нее можно использовать некоторые простые соображения, связанные с природой задачи. Например, если рассматриваемая в Rn дифференцируемая функция по смыслу задачи должна иметь минимум и вместе с тем она не ограничена сверху, то при условии, что функция имеет единственную критическую точку, можно без дальнейшего исследования утверждать, что в этой точке она принимает минимальное знычение.

6.Условный экстремум. 6.1.Постановка вопроса.

Одним из наиболее ярких популярных достижений дифференциального исчисления являются предполагаемые им рецепты отыскания экстремумов функций. Необходимые условия и достаточные дифференциальные признаки экстремума, которые мы получили из формулы Тейлора, относятся, как уже отмечалось к внутренним экстремумам.

Иными словами, эти результаты применимы только к исследованию поведения функции Rn x f(x) R в окрестности точки тогда, когда аргумент может принимать любое значение из некоторой окрестности Rn в точки x0.

Часто возникает более сложная и с практической точки зрения даже более интересная ситуация,когда ищется экстремум функции при некоторых условиях, ограничивающих область измерения аргумента. Типичным примером может служить изопериметрическая задача, когда ищется тело, имеющее максимальный объем при условии, что ограничивающая его поверхность имеет заданную площадь. Чтобы получить доступную нам математичкую запись такой задачи, упростим постановку и будем считать, что задача состоит в том, чтобы среди прямоугольников, имеющих заданный периметр 2р, найти тот, который имеет наибольшую площадь . Обозначив через х и у длины сторон прымоугольника, запишем, что

(х,у)=х-у

х+у=р

Итак, надо найти экстремум функции (х,у) при условии, что переменные х,у связаны соотношением х+у=р. Таким образом, экстремум функции ищется только на множестве тех точек плоскости R2, которые удовлетворяют указанному соотношению. Эта конкретная задача, конечно, решается без труда : достаточно, записав, что у=р-х, подставить это выражение в формулу для (х,у) и найти обычными методами максимум функции х(р-х). Она нам была нужна лишь для постановки вопрса. В следующих пунктах мы рассмотрим общий случай решения подобных задач.

6.2.Понятие условного экстремума.

Пусть на открытом множестве G Rn заданы функции.

yi=fi(x) i=1,2,3,…,m (6.1)

x=(x1,x2,…,xn).Обозначим через Е множество точек x G , в которых все функции fi i=1,2,3,…,m обращаются в нуль:

E={x: fi(x)=0, i=1,2,3,…,m, x G} (6.2)

Уравнения

fi(x)=0, i=1,2,3,…,n (6.3)

будем называть уравнениями связи.

Определение : пусть на множестве G задана функция y=f0(x) .Тогда x(0) E называется точкой условного экстремума (принят также термин “относительный экстремум”) функции f0(x) относительно (или при выполнении) уравнений связи (6.3) , если она является точкой обычного экстремума этой функции , рассмотриваемой только на множестве Е.

Иначе говоря , здесь значения функции f0(x) в точке x(0) сравниваются не со всеми ее значениями в достаточно малой окрестности этой точки , а только со значениями в точках , принадлежащих одновременно указанной достаточно малой окрестности и множеству Е. Как и в случае обычных экстремумов , можно , естественно , рассматривать точки просто условного экстремума и точки строго условного экстремума.

Будем предполагать , что

все функции f0,f1,f2,…, fm непрерывно дифференцируемы в открытом множестве G ; в рассматриваемой точке x(0) векторы f1, f2,…, fm линейно независимы , т.е. ранг матрицы Якоби

fj j=1,2,…,m

xi i=1,2,…,n

равен m-числу ее строк (строки матрицы Якоби являются компонентами градиентов f1, f2,…, fm).

Это означает , что функции системы (6.1) независимы в некоторой окрестности точки x(0).Поскольку в n-мерном пространстве не может быть больше чем n линйено независимых векторов и ранг матрицы не может быть больше чиола столбцов , то из условия 2) следует ,что m<n.

Согласно условию 2) в точке x(0) хотя бы один из определителей вида

(f1, f2,…, fm)

(xi1,xi2,…,xim)

отличен от нуля.Пусть для определенности в точке x(0).

(f1, f2,…, fm)

(xi1,xi2,…,xim) (6.4)

Тогда , в силу теоремы о неявных функциях , систему уравнений (6.3) в некоторой окрестности точки x(0)=(x1(0),x2(0),…,xn(0)) можно разрешить относительно переменных x1,x2,…,xm :

x1= 1( x1,x2,…,xm)

x2= 2( x1,x2,…,xm)

…………………… (6.5)

xm= m( x1,x2,…,xm)

Поставив значения x1,x2,…,xm, даваемые формулами (6.5) в y=f0(x), т.е. рассмотрев композицию функции f0 и 1, получили функцию

y= f0(1( xm+1,…,xn),…, m( xm+1,…,xn), xm+1,…,xn)==0( xm+1,…,xn) (6.6)

от n-m переменных xm+1,…,xn,определенную и непрерывно дифференцируемую в некоторой окрестности точки x(0)=(x1(0),x2(0),…,xn(0)) в (n-m)–мерном пространстве Rn-m.

Поскольку , согласно теореме о неявных функциях , условия (6.3) и (6.5) равносильны ,то справедливо следующее утверждение.

Точка x(0) является точкой (строгого) условного экстремума для функции g относительно уравнений связи (6.3) в том и только том случае , когда x(0) является точкой обычного (строгого) экстремума (6.6).

Если x(0)– точка обычного экстремума функции g, то она является стационарной точкой этой функции:

dg (x(0))=0 (6.7)

Напомним , что дифференциал – линейная однородная функция и его равенство нулю означает равенство нулю этой функции при любых значениях ее аргументов , в данном случае – при любых dxm+1, dxm+2,…, dxn.Это возможно ,очевидно , в том и только том случае , когда все коэффициенты при этих аргументах , т.е. производные g/ xm+k, k=1,2,…,n-m обращаются в нуль в точке x(0).Условие (6.7) необходимо для условного экстремума в точке x(0).

Таким образом , метод , основанный на решение системы уравнений (6.3) через элементарные функции часто невозможно или весьма затруднительно; поэтому желательно располагать методом , позволяющим найти условный экстремум не решая системы (6.3).Такой способ ,так называемый метод множетелей Лагранжа , изложен в следующем пункте .

6.3.Метод множетелей Лагранжа для нахождения точек условного экстремума.

В этом пункте будем предполагать , что все функции f0,f1,f2,…, fm непрерывно дифференцируемы в открытом множестве G.

Теорема 6.1 : пусть x(0)– точка условного экстремума функции f0 при выполнении уравнений связи (6.3).Тогда в этой точке градиенты f1, f2,…, fm линейно независимы , т.е. существуют такие не все равные нулю , числа 0, 1, 2,…, m что