Навигация
F0+ 1f1+ 2f2+…+ mfm=0 (6.8)
0 f0+ 1f1+ 2f2+…+ mfm=0 (6.8)
Следствие : если в точке x(0) условного экстремума функции f0 относительно уравнений связи (6.3) градиенты f1, f2,…, fm линейно независимы , то ранг матрицы Якоби
fj j=1,2,…,m
xi i=1,2,…,n
равен m, то существуют такие 1,…, m , что в этой точке
f0+ i fj=0 (6.9)
т.е. f0 является линейной комбинацией градиентов f1, f2,…, fm.
В координатной форме это условие имеет вид : для любого i=1,2,…,n в точке x(0)
f0 fi
xi xi (6.10)
функция
F(x)==f0(x)+ jfj(x) (6.11)
где числа 1,…, m удовлетворяют условию(6.10), называется функцией Лагранжа рассматриваемой задачи , а сами числа 1,…, m – множителями Лагранжа.
Условие (6.10) означает , что если x(0) является точкой условного экстремума функции f0 относительно уравнений связи (6.3) , то она является стационарной точкой для функции Лагранжа , т.е.
F(x(0))
xi i=1,2,…,n (6.12)
Прежде , чем доказать теорему , разъясним ее смысл и покажем , как ее использовать для нахождения точек условного экстремума. Прежде всего обратим внимание на то , что у функции вида (6.11) при произвольных числах 1,…, m, каждая точка ее условного экстремума является и точкой условного экстремума исходной функции f0, и наоборот.Мы выбираем такие значения 1,…, m, чтобы выполнялись условия (6.10) , т.е. чтобы данная точка условного экстремума оказалась и стационарной точкой фуцнкции (6.9).
Для отыскания точек условного экстремума следует рассмотреть систему n+m уравнений (6.3) и (6.8) относительно неизвестных x1(0),x2(0),…,xn(0), 1,…, m и решить ее (если это возможно) , найдя x1(0),x2(0),…,xn(0) и по возможности исключив 1,…, m.Сформулированная теорема утверждает , что все точки условного экстремума будут находится среди найденных таким образом точек (x1(0),x2(0),…,xn(0)).Вопрос о том , какие же из них фактически будут точками условного экстремума , требует дополнительного исследования , об этом будет говориться в п.6.5
Доказательство теоремы . Докажем утверждение равносильное теореме : если в точке x(0)=(x1(0),x2(0),…,xn(0)), удовлетворяющей уравнениям связи
fk(x(0))=0 k=1,2,…,n (6.13)
градиенты f0, f1, f2,…, fm линейно независимы , то x(0) не является точкой условного экстремума.
Итак , пусть f0, f1, f2,…, fm линейно независимы и , следовательно , ранг матрицы Якоби fj/ xi j=1,2,…,m,i=1,2,…,n равен m+1.Тогда в матрице существует минор порядка m+1 не равный нулю.Для определенности будем считать , что он образован первыми m+1 столбцами , т.е.
(f0, f1, f2,…, fm)
(x1,x2,…,xm+1) x=x(0) (6.14)
Множество G–открыто , а поэтому существует такое 00>0, что при всех 0 0<0<00 , куб
Q n={x: xi-xi(0) <0,i=1,2,…,n}
лежит в G и , следовательно, на нем определены все функции f0, f1, f2,…, fm.
Зафиксируем xm+2= x(0)m+2,…, xn=xn(0) и введем обозначения
x*=(x1,x2,…,xm+1)
Q m+1={x*: xi-xi(0) <0,i=1,2,…,m+1}
Очевидно , функции fj(x1,x2,…,xm+1,x(0)m+2,…,xn(0)) j=1,2,…,m определены и непрерывно дифференцируемы всюду в Q m+1.Рассмотрим отображение Ф : Q m+1 Rm+1, задаваемое формулами
y1= f0(x1,x2,…,xm+1,x(0)m+2,…,xn(0))
y2= f1(x1,x2,…,xm+1,x(0)m+2,…,xn(0))
…………………………………… (6.15)
ym+1= fm(x1,x2,…,xm+1,x(0)m+2,…,xn(0))
В силу (6.15) для точки x*(0)=(x1(0),x2(0),…,xn(0)) имеем
(y1, y2,…, ym+1) (f0, f1, f2,…, fm)
(x1,x2,…,xm+1) x*= x*(0) (x1,x2,…,xm+1) x=x(0)
а в силу (6.13) Ф(x*(0))=(f0(x(0),0,…,0) .Поэтому (в силу теремы о локальной обратимости непрерывно дифференцируемого отображения в точке , в которой его якобиан не равен нулю , существует такое число >0 , что на окрестности
V={y=(y1, y2,…, ym+1) : y1- f0(x(0)) < , yj< ,j=2,3,…,m}
В частности , поскольку при любом n,0<n< ,имеет место включение (f0(x(0))+n,0,…,0), то в кубе найдутся точки x`*=(x`1,x`2,…,x`m+1) и x``*=(x``1,x``2,…,x``m+1), отображающиеся при отображении Ф в указанные точки окрестностиV`.
Ф(x`*)=(f0(x(0))+n,0,…,0)
Ф(x``*)=(f0(x(0))-n,0,…,0)
Если положим для краткости x`=(x`1,x`2,…,x`m+1,x(0)m+2,…,xn(0)) и x``=(x``1,x``2,…,x``m+1,x(0)m+2,…,xn(0)), то в координатной записи (6.15) получим
f0(x`)= f0(x(0))+n> f(x(0)) , fk(x`)=0, k=1,2,…,n , x` Q n
и
f0(x``)= f0(x(0))-n> f(x(0)) , fk(x``)=0, k=1,2,…,n , x`` Q n
В силу произвольности 0>0,0<0<0 , это и означает , что x(0) не является точкой условного экстремума.
ч.т.д.
Доказательство следствея. Если векторы f1, f2,…, fm линейно независимы , то в равенстве (6.8) имеем 0=0 так как в случае 0=0 указанные векторы в силу (6.8) оказались бы линейно зависимыми .Разделив обе части на 0 получим равенство вида (6.9).
ч.т.д.
Пример №5.
Пусть требуется найти экстремум функции u=xyzt при условии x+y+z+t=4c; область изменения переменных определяетссся неравенствовами x>0, y>0, t>0, z>0.
Применяя к этой задаче метод Лагранжа, введем вспомогательную функцию
Ф=xyzt+ (x+y+z+t)
И составим условия
Фx =yzt+ =0
Фy =xzt+ =0
Фz =yxt+ =0
Фt =yzx+ =0
откуда
yzt=xzt=xyt=xyz
так что
x=y=z=t=c.
6.4.Стационарные точки функции Лагранжа.В этом пункте будет дано описаие стационарных точек функции Лагранжа (6.10) посредством фукции 0(xm+1,xm+2,…,xn), введенной в пункте 6.2 (см.(6.8)).Предварительно докажем одну простую лемму из линейной алгебры.
Пусть задана система линейных однородных уравнений
ai1x1+…+ ainxn=0 i=1,2,…,m (6.16)
и еще одно линейное однродное уравнение
b1x1+…+ bnxn=0 (6.17)
Cистему уравнений , полученную присоединением к системе (6.16) уравнения (6.17), будем называть расширенной системой (6.16)-(6.17).
Лемма: Для того чтобы расширенная система (6.16)-(6.17) была равносильна основной системе (6.16) необходимо и достаточно , чтобы уравнение (6.17) являлось линейной комбинацией уравнений системы (6.16).
Следствие:Для того чтобы уравнение (6.17) было линейной комбинацией уранений (6.16) или , что то же самое , чтобы вектор
b==(b1,…,bn) (6.18)
был линейной комбинацией векторов
ai ==(ai1,…,ain) i=1,2,…,m (6.19)
необходимо и достаточно , чтобы каждое решение системы (6.16) являлось решением уравнения (6.17).
Доказательство леммы . Пусть ранг матрицы (aij) коэффициентов системы (6.16) равен m0 . Очевидно , что m0<m . Если m0<m, то уравнений системы (6.16) являются линейными комбинациями остальных. Отбросив те m-m0 линейных уравнений , которые являются линейными комбинациями оставшихся , получили систему из m0 линейно независимых уравнений . равносильную системе (6.16), причем уравнение (6.17) является линейной комбинацией уравнений системы (6.16) тогда и только тогда , когда оно является линейной комбинацией указанной системы из оставшихся m0 уравнений. Поэтому будем с самого начала считать , что , m0=m т.е. что ранг матрицы (aij) коэффициентов системы (6.16) равен m– числу уравнений этой системы.
Пусть система (6.16) и (6.16)-(6.17) равносильны. Это означает, что пространства их решений совпадают.Поскольку все уравнения основной системы (6.16) входят в расширенную систему (6.16)-(6.17), то каждое решение расширенной системы является и решением основной системы , т.е. пространство решений расширенной системы содержится в пространстве решений основной системы. Следовательно , слвпадение этих пространств равносильно равенству их размерностей.
Размерность s пространства решений системы линейных днородных уравнений равны , как известно , числу неизвестных n этой системы , из которого вычтем ранг r матрицы коэффициентов системы : s=n-r.Отсюда следует , что равносильность систем (6.16) и (6.16)-(6.17) означает равенство рангов их матриц.Ранг матрицы коэффициентов системы (6.16) по условию равен m , т.е. векторы (6.19) линейно независимы.
Ранг матрицы коэффициентов расширенной системы (6.16)-(6.17) согласно сказанному в наших условиях также равен m.Поэтому векторы (см.(6.18) и (6.19))
b, a1,…, am (6.20)
линейно зависимы.А это означает , что b является линейной комбинацией векторов a1,…, am.
В самом деле , линейная зависимость векторов (6.20) означает , что существуют такие числа 0, 1,…, m, не все равные нулю . что
0b+ 1a1+…+ mam=0 (6.21)
Здесь заведамо 0=0, так как в противном случае векторы a1,…, am оказались бы линейно зависимыми. Поделив равенство (6.21) на 0, получим , что b является линейной комбинацией векторов a1,…, am .
Обратно, если b является линейной комбинацией векторов (6.19), то в системах векторов (6.19) и (6.20) имеется в точности по m линейно независимых векторов , т.е. ранги матриц коэффициентов систем уравнений (6.16) и (6.16)-(6.17) равны.
Итак, условие , что вектор b является линейной комбинацией векторов (6.19) :
1a1+…+ mam=b
эквивалентно равенству рангов матриц коэффициентов рассматриваемых основной и расширенной системв уравнений, следовательно, эквивалентно их равносильности.
ч.т.д.
Доказательство следствия сразу следует из леммы, поскольку системы (6.16) и (6.16)-(6.17) очевидно равносильны тогда и только тогда , когда каждое решение системы (6.16) является и решением уравнения (6.17) – остальные уравнения систем просто совпадают.
ч.т.д.
Замечание 1 : доказанная лемма и ее следствие имеют простую геометрическую интерпритацию в n–мерном евклидовом векторном пространстве Rn, т.е. в n–мерном пространстве со скалярным произведением.Используя обозначение скалярного произведения, систему (6.16) можно записать в виде
(ai,x)=0 i=1,2,…,m (6.22)
а уравнение (6.17) в виде
(b,x)=0 (6.23)
где векторы a1,…, am и определены в (6.18) и (6.19) , а x=(x1,x2,…,xm+1)
Множество всевозможных линейных комбинаций векторов a1,…, am образуют подпространство пространства Rn и называется подпространством, натянутым на эти векторы.Обозначим его через Z=( a1,…, am).
Множество решений системы (6.22) состоит из всех векторов х, ортоганальных подпространству Z=( a1,…, am) Обозначим это множество решений через Т.Оно также является подпространством пространства Rn.
Подпространства L==Z(a1,…, am) и Т называются ортоганальными дополнениями друг друга в пространстве Rn.
Поскольку L=Z( a1,…, am), то представимость вектора b в виде линейной комбинации векторов a1,…, am равносильна его принадлежности подпространству L пространства Rn:b L.Это условие в свою очередь, равносильно ортоганальности вектора b подпространству Т:b _Т, которая означает, что для всех x Т имеет место равенство (b,x)=0,т.е.что любое реение х системы (6.22) является решением уравнения (6.23).Это и является утверждением следствия леммы.
Замечание 2 : напомним метод, которым можно получить все решения однородной системы линейных уравнений.Пусть система (6.16) состоит из линейно независимых уравнений.Тогда ранг матрицы его коэффициентов равен m.Это означает , что существует минор этой матрицы порядка m, не равный нулю.Пусть для определенности
a11… a1m
am1… amm (6.24)
В этом случае все решения системы (6.16) можно получить , задавая произвольно последние n-m координаты вектора (x1,x2,…,xn). Остальные координаты однозначно находятся из системы уравнений (6.16).В самом деле, возьмем произвольное решение (x1(0),x2(0),…,xn(0)) системы (6.16).После подстановки xm+1= x(0) m+1,…, xn= xn(0) в (6.16) получится система из m линейных уравнений (с m неизвестными x1,x2,…,xn), матрицы коэффициентов которой в силу условия (6.24) невырожденная.Поэтому существуют единственные значения x1,x2,…,xn, удовлетворяющие получившейся системе.Поскольку (x(0)1,x(0)2,…,x(0)n). также было решением системы (6.16), то x1=x(0)1, x2=x(0)2,…, xm=x(0)m .
Перейдем теперь к анализу стационарных точек функции Лагранжа.
Теорема 6.2: Пусть функции f0, f1, f2,…, fm непрерывно дифференцируема в области G Rn, x(0) G
fi(x)=0, i=1,2,3,…,n
а ранг матрицы Якоби функций f1, f2,…, fm в точке x(0) равен m.Для того чтобы в точке x(0)=(x(0)1,x(0)2,…,x(0)n) градиент f0 являлся линейной комбинацией градиентов f1, f2,…, fm необходимо и достаточно, чтобы точка x(0)=(x(0)1,x(0)2,…,x(0)n) была стационарной точкой для функции.
g(x)=g(xm+1,…,xn)
Напомним,что если в точке x(0) градиент f0 является линейной комбинацией
f0= 1f1+ 2f2+…+ mfm (6.25)
градиентов f1, f2,…, fm, то это равносильно тому, что существует функция Лагранжа
F= f0- 1f1- 2f2-…- mfm (6.26)
для которой точка x(0) является стационарной :
F(x(0))
xi i=1,2,…,n (6.27)
Это просто координатная запись (6.25) ,ибо в силу (6.26)
F(x(0)) f0 f1 f2 fm
xi xi xi xi xi i=1,2,…,m
Доказательство: По условию ранг матрицы Якоби системы функций f1, f2,…, fm в точке x(0) равен m .Будем считать для определенности , как и в пункте 6.2 ,что
(f1, f2,…, fm)
(x1,x2,…,xm) x(0) (6.28)
Подставим в уравнение связи (6.3) функции (6.5) , являющиеся решением этих уравнений , и продеффиренцируем получившееся относительно переменных xm+1,…,xn тождества.Получим для точки x(0) равенства dfi(x(0))=0, i=1,2,…,m, справедливые для любых приращений dxm+1,…,dxn независимых переменных xm+1,…,xn (напомним, что дифференциал являетсся линейной функцией , определенной на всем пространстве)Использовав инвариантность формы первого дифференциала относительно выбора переменных , получим , что в точке выполняется равенство
fi fi fi fi i=1,2,…,m
x1 xm xm+1 xn (6.29)
где xm+1,…,xn произвольные , а x1,…,xm находятся изформул (6.5). Таким образом вектор dx=( dx1,…,dxm,dxm+1,…,dxn) является решением линейной однородной системы (6.29).
Отметим , что в силу условия (6.28) значения dx1,…,dxm при заданных dxm+1,…,dxn однозначно находятся и из системы (6.29). Из замечания 2 следует также , что указанным способом получаются все решения системы (6.29).
Стационарность точки x(0) для функции g(x)=g(xm+1,…,xn)
означает , что dg(x(0)).Это равенство , в силу инвариантности формы первого дифференциала, можно более подробно записать в виде
f0 f0 f0 f0
x1 xm xm+1 xn (6.31)
где dxm+1,…,dxn можно задавать произвольно, а dx1,…,dxm следует находить из формул (6.5) или , что дает тотже результат из формул (6.29). Инач говоря , любое решение системы уравнений (6.29) является и решением уравнения (6.31). Согласно следствию из леммы это возможно тогда и тoлько тогда , когда уравнение (6.31) является линейной комбинацией уравнений системы (6.29) , т.е. когда существуют такие числа , что
f0= 1f1+ 2f2+…+ mfm
ч.т.д.
Замечание 3 : Согласно замечанию 2 совокупность всех решений систеиы уравнений (6.29) образуют подпространство Т пространства Rn, являющееся ортогональным дополнением к подпространству L=Z( f1, f2,…, fm) . Любой вектор y T ортогонален каждому градиенту fi , а поэтому его естественно назвать касательным вектором в точке x(0) к гиперповерхности fi(x)=0 , являющиеся множеством уровня функций fi,i=1,2,…,m.
Таким образом , пространство решений Т системы (6.29) состоит из векторов , касательных одновременно ко всем гиперповерхностям fi(x)=0 ,i=1,2,…,m, и потому его называют касательным пространством персечений всех гиперповерхностей fi(x)=0 ,i=1,2,…,m . Напомним , что векторы касательноо пространства Т ,т.е. решения системы (6.29), были обознаены через dx (см.(6.30)).
Поскольку в точке условного экстремума согласно теореме 2 имеет место включение
f0 L=Z( f1, f2,…, fm)
то
f0 T
Иначе говоря, градиент f0 одновременно ортогонален всем касательным dx к гиперповерхностям fi(x)=0 ,i=1,2,…,m:
( f0,dx)=0
(это другая запись уравнения (6.31)), т.е. градиент f0 перпендикулярен касательному пространству Т в точке x(0) .Но множество всех векторов , ортогональных к f0, образуют (n-1)– мерное пространство Т0 , называемое касательным пространством к гиперповерхности f0(x)= f0(x(0)) .В силу сказанного выше , каждый вектор из Т , будучи ортогонален градиенту f0, принадлежит к Т0 , т.е. Т Т0.
Итак , если x(0) – точка условного экстремума , то . Т Т0 , т.е. касательное пространство в точке x(0) пересечения всех гиперповерхностей , задаваемых уравнениями связи , содержится в касательном пространстве в той же точке гиперповерхности.
Замечание 4 : Из теоремы 2 еще раз вытекает следствие теоремы 1.В самом деле , если x(0) является точкой условногo экстремума , то является x(0) точкой обычного экстремума для функции () и , следовательно , ее стационаоной точкой . Поэтому согласно теореме 2 точка x(0) является стационарной точкой для функции Лагранжа , т.е.выполняется условие .
6.5.Достаточные условия для точек условного экстремума.В этом пункте также будем предполагать выполненными все предположения , наложенные на функции в пункте 6.2.Пусть
F= f0+ ifi
-функции Лагранжа (см.(6.11)) для функции f0 и уравнений связи(6.3).Пусть x(0) G удовлетворяет уравнениям связи (6.3) и является стационарной точкой функции Лагаранжа , т.е. точкой , координаты которой удовлетворяют системе уравнений (6.10) и (6.3). Нашей целью является получение метода , с помощью которого можно установить условия , достаточные для того , чтобы x(0) являлась точкой условного экстремума рассматриваемой задачи.
Заметим прежде всего , что если точка x G удовлетворяет уравнениям связи (6.3) , то
f= f(x)-f(x(0))=F(x)-F(x(0))= F (6.32)
Отсюда сразу видно , что если x(0) является точкой обычного экстремума для функции F, т.е. F не меняет знака в некоторой окрестности точки x(0), то x(0) является точкой условного экстремума для функции f0 .
Действительно , из (6.32) следует в этом случае , что приращение f0 для допустимых значений х , т.е. удовлетворяющих уравнениям связи , также не меняет знак, Это достаточное условие , однако , накладывает слишком сильное ограничение на поведение функции Лагранжа F(x) в рассматриваемой точке – она должна иметь обычный экстремум , что сильно сужает область возможного применения указанного условия при решении задач.Поэтому целесообразно получить более общий достаточный признак условного экстремума .
Пусть x(0)= (x(0)1,x(0)2,…,x(0)n) удовлетворяет уравнениям связи (6.3).Вернемся к рассмотрению функции (6.6) , т.е. функции g(x)=g(xm+1,…,xn) , получаемой из f0(x)= f0(x1,x2,…,xn) при условии , что являются x1,x2,…,xm функциями переменных xm+1,…,xn определяемых уравнениями связи (6.3) в некоторой окрестности точки x(0).Будем дополнительно предполагать , что f0(x ) и fi(x ) ,i=1,2,…,m дважды непрерывно дифференцируема в точке x(0).
Выше отмечалось (в пункте 6.2) , что x(0) является точкой условного (строгого) экстремума для функции f0(x) относительно уравнений связи (6.3) тогда и только тогда , когда x(0) является точкой обычного (строгого) экстремума для функции g(x).Поэтому , если например , в точке x(0) функция g(x) удовлетворяет достаточным условиям существования строгого экстремума,то в этой точке функция f0(x) имеет условный строгий экстремум относительно уравнений связи (6.3).Достаточные условия для обычного сторого экстремума были получены нами ранее .Для нашего случая они имееют вид :
g(x(0) )xi i=m+1,…,n; (6.33)
2)второй дифферециал
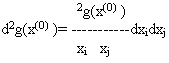
является положительно или отрицательно определенной квадратичной формой.
При выполнении этих условий x(0) является точкой строгого минимума или максимума для функции g(x).В силу сказанного выше указанные условия являются и достаточными условиями для того, чтобы x(0) являлось точкой условного строго минимума (максимума) для функции f0(x) относительно уравнений связи (6.3). Однако они неудобны для практического использования , так как требуют знания функции g(x).Поэтому , исходя из полученных достаточных условий условного строгого экстремума , выраженных посредством функции g(x) , получим достаточные условия того же экстремума , но выраженные только через функцию Лагранжа и уоавнений связи.
Прежде всего заметим , что в силу условия (6.4) система (6.29) разрешима, и притом однозначно, относительно dx1,…,dxm при произвольно фиксированных dxm+1,…,dxn .Систему (6.29), выражающую равенство нулю дифференциалов функции fi(x) в точке x(0):
d fi(x)=0, i=1,2,…,m
при выполнении условий (6.3) , будем записывать кратко в виде :
df=0 (6.35)
где
f=(f1,f2,…,fm)
Пусть x(0) является стационарной точкой для функции Лагранжа F(x).Это означает, что dF(x(0))=0, т.е. что в этой точке f0+ ifi=0.В теореме 2 показано, что в том случае x(0) является стационарной точкой для функции, т.е.
dg(x(0))=0 (6.36)
Поясним еще раз вывод этой формулы и покажем, что
d2g(x(0) )= d2F(x(0) ) df=0 (6.37)
Это равенство следует понимать как равенство функции n-m переменных dxm+1,…,dxn.В правой части равенства (6.37) остальные переменные dx1,…,dxm, которые входят в выражения написанных дифференциалов, определяются из системы уравнений (6.35) или, что равносильно (см. формулы (6.5))
dxk=d k(x1,x2,…,xn-m), k=1,2,…,m
Используя инвариантность формы первого дифференциала относительно выбора переменных и формулу (6.6), имеем
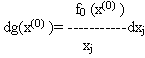
Прибавим к этому равенству сумму (равную нулю) левых частей тождеств (6.29), умноженных соответственно на постоянные i, входящие в функцию Лагранжа F(x) (точнее, i-е равенство (6.29) умножается на постоянную i).Тогда, использовав условие (6.11), получим
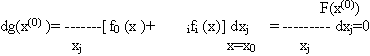
Утверждение (6.36) доказано.
Равенство (6.37) доказывается аналогичным приемом.Прежде всего напишем второй дифференциал для функции g(x) в точке x(0):
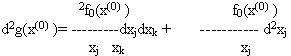
Далее продифференцировав тождества, получающиеся в результате дифференцирования уравнений связи (6.3), т.е. тождества будем иметь в точке x(0) :
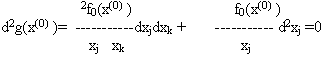
i=1,2,…,n
Умножив i–е равенство (6.39) на постоянную i, входящую в функцию Лагранжа F(x), прибавим получившееся выражение к правой части равенства (6.38) ; тогда получим

где dxi, i=1,2,…,n удовлетворяет системе уравнений (6.35).Поскольку x(0) точка стационарная для функции Лагранжа, то второй член получившегося равенства обращается в нуль, и тем самым формула (6.37) доказана.
Будем говорить, что квадратичная форма d2F(x(0) ) является положительно (отрицательно) определенной квадратичной формой переменных dxi, i=1,2,…,n, при условии, что эти переменные удовлетворяют системе уравнений (6.35), если для любых dxi, i=1,2,…,n , удовлетворяющих этой системе уравнений и таких, что (dxi)2>0 выполняется неравенство d2F(x(0) ) >0 (соответственно d2F(x(0) ) <0)
Пусть точка x(0) удовлетворяет уравнениям связи (6.3) и является стационарной для функции Лагранжа (6.11) и пусть второй дифференциал функции Лагранжа в этой точке является положительно (отрицательно) определенной квадратичной формой переменных dx1,…,dxn, при условии, что они удовлетворяют системе уравнений (6.35).Тогда из (6.36) и (6.37) следует, что x(0) является стационарной точкой для функции g(x) и что второй дифференциал этой функции в точке x(0) является положительно (отрицательно) определенной квадратичной формой переменных dxm+1,…,dxn, и, следовательно, функция имеет в точке x(0) строгий минимум (максимум) , а значит, функция f0(x) имеет в точке x(0) условный строгий минимум (максимум) относительно уравнений связи (6.3).
Сформулируем полученный результат в виде теоремы.
Теорема 6.3: Если x(0) удовлетворяет уравнениям связи (6.3) и является стационарной точкой для функции Лагранжа (6.11) и если второй дифференциал функции Лагранжа в этой точке является положительно (отрицательно) определенной квадратичной формой переменных dx1,…,dxn при условии, что они удовлетворяют системе уравнений (6.29), то x(0) является точкой строгого минимума (максимума) для функции f относительно уравнений связи (6.3).
Таким образом, чтобы исследовать стационарную точку функции Лагранжа (6.11) на условный экстремум, надо исследовать на определенность квадратичную форму (6.37), т.е. второй дифференциал функции Лагранжа в этой точке при выполнении условий связи (6.3) (когда дифференциалы dxi, i=1,2,…,n связаны соотношениями (6.29)).При этом следует иметь в виду, что если второй дифференциал функции Лагранжа в рассматриваемой точке окажнтся положительно (отрицательно) определенным и без выполнения условий связи, то он будет и таковым , конечно, и при их выплнении.
7.Заключение.Математический анализ это совершенно естественная, простая и элементарная наука, ничуть не более заумная, сложная или “высшая”, чем, скажем, “элементарная” геометрия. Многие теоремы, традиционно входившие в курс геометрии, куда сложнее, чем основополагающие теоремы классического анализа. Ныне противопоставление элементарной математики и анализа непродуктивно, и вовсе необязательно проявлять бездну остроумия только лишь из боязни использовать свойства производной.
Привнесение элементов математического анализа в школьные программы неизбежно приведет к перестройке и других областей математического образования – изменится содержание конкурсных задач, кружковой работы, математических олимпиад и многого другого. Теперь уже невозможно не учитывввать, что школьник должен знать нечто из ранее недоступной ему высшей математики.
При этом следует иметь в виду, что если освоены лишь самые основы математического анализа, можно уже делать попытки подобраться ко многим современным проблемам.
При рассмотрении данной темы дипломного проекта теоритические сведения подтвердились практическим доказательством и математическим обоснованием.
8. Библиография.1.А.Ф.Бермант, И.Г.Араманович Краткий курс математического анализа.-М.: Наука, 1973.
2.И.Е.Жак Дифференциальное исчисление.-М.:Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1960.
3.Г.И.Запорожец Руководство к решению задач по математическому анализу.-М.: Высшая школа,1966.
4.В.А.Зорич Математический анализ.-М.: Наука, 1981.
5.А.П.Картышев, Б.Л.Рождественский Математический анализ.-М.: Наука, 1984.
6.А.Н.Колмогоров, С.В.Фомин Элементы теории функций и функционального анализа.-М.: Наука, 1981.
7.Л.Д.Кудрявцев Курс математического анализа.-М.: Высшая школа, 1981.
8.А.Г.Моркович, А.С.Солодовников Математический анализ.-М.: Высшая школа, 1990.
9.Н.С.Пискунов Дифференциальное и интегральное исчисление. т.1.-М.: Наука, 1978.
10.К.А.Рыбников История математики.-М.:Издательство Московского университета, 1994.
11.В.М.Тихомиров Рассказы о максимумах и минимумах.-М.:Наука, 1986.
12.Г.М.Фихтенгольц Основы математического анализа. т.2.-М.: Наука, 1968.
13.Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления. т.1.-М.: Наука, 1969.
Похожие работы
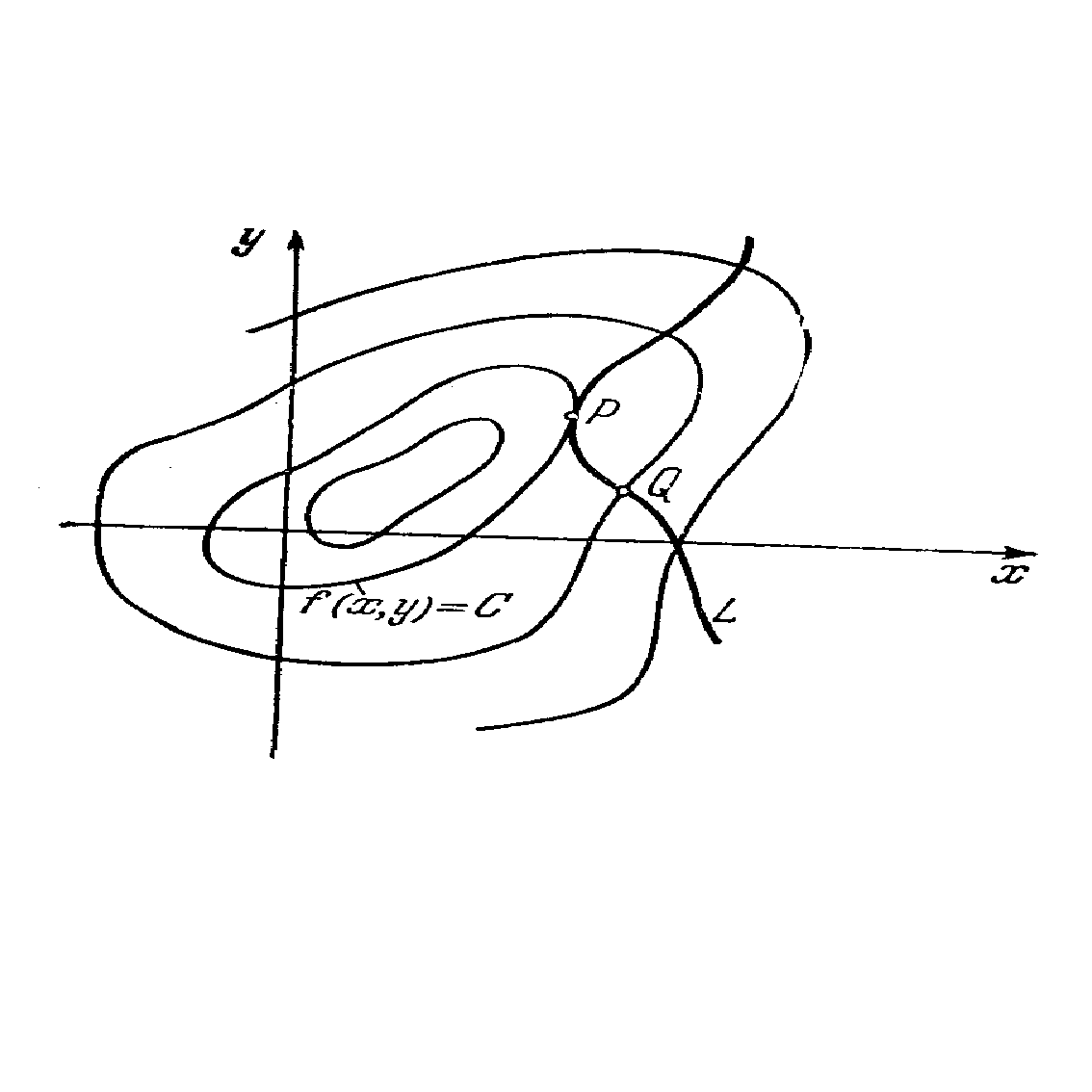
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... Для U = f(x,y, z) в точке Мо (хо ,уо, zо) будет выполнено условие . Замечание. Точку, в которой частные производные первого порядка либо не существуют, либо равны нулю, называют критической. Т.е. экстремумы функции нескольких переменных могут достигаться лишь в критических точках. Пример 15.1. Покажем, что указанные выше условия не являются достаточными. Пусть z = f(x, y) = x × y тогда ...
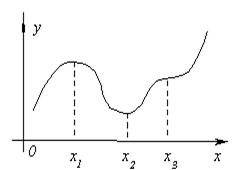
... b). Тогда, если f'(x) > 0, х Î (a, b), то f(x) строго монотонно возрастает на (a, b). Если же f'(x) < 0, х Î (a, b), то f(x) строго монотонно убывает на (a, b). 2. ИССЛЕДОВАНИЕ ФУНКЦИЙ 2.1 Достаточные условия экстремума функции В лекции 1 мы рассмотрели основные теоремы математического анализа, которые широко используются при исследовании функции, построении ее графика. ...
... . Пример 5. Найти частные производные второго порядка функции . Решение. Частные производные первого порядка для данной функции найдены в примере 3: Дифференцируя и по переменным х и y, получим , ; ; . 5. Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума Определение 7. Точка называется точкой минимума (максимума) функции ...

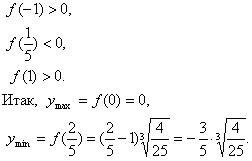
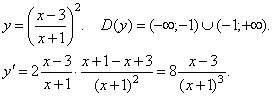
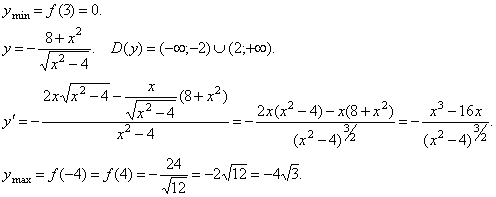
0 комментариев