Навигация
0 £ xk £ x
для k = 2, 3, 4, ... , n . Если же k=1, то
F1(x ) = f1(x )
Рассмотрим конкретный пример. Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций fj(xj) приведены в таблице 1, где, например, число 88 означает, что если третье предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 88 тыс. руб.
Таблица I
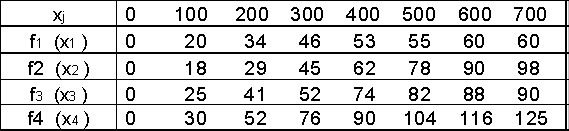
Прежде всего заполняем табл. 2. Значения f2(x2) складываем со значениями F1(x - x2) = f1(x - x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение ![]() . Заполняем таблицу 3.
. Заполняем таблицу 3.
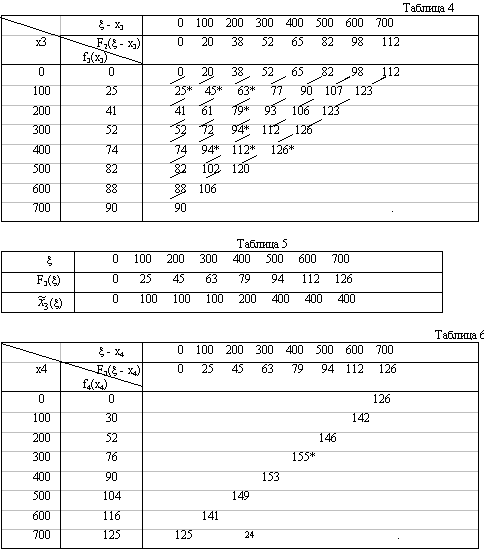
Продолжая процесс, табулируем функции F3(x ), ![]() (x ) и т.д. В табл. 6 заполняем только одну диагональ для значения x = 700. Наибольшее число на этой диагонали:
(x ) и т.д. В табл. 6 заполняем только одну диагональ для значения x = 700. Наибольшее число на этой диагонали:
Zmax = 155 тыс. руб.,
причем четвертому предприятию должно быть выделено
х*4 = ![]() 4 (700) = 300 тыс. руб.
4 (700) = 300 тыс. руб.
На долю остальных трех предприятий остается 400 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено
x*3 = ![]() 3 (700-x*4) =
3 (700-x*4) = ![]() 3 (400) = 200 тыс. руб.
3 (400) = 200 тыс. руб.
Продолжая обратный процесс, находим
x*2 = ![]() 2 (700 - x*4 - x*3) =
2 (700 - x*4 - x*3) = ![]() 2 (200) = 100 тыс. руб.
2 (200) = 100 тыс. руб.
На долю первого предприятия остается
x*1 = 700 - x*4 - x*3 - x*2 = 100 тыс. руб.
Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:
x*1 =100; x*2 =100; x*3 = 200; x*4 = 300.
Оно обеспечивает производственному объединению наибольший воможный прирост прибыли 155 тыс. руб.
Студенту рекомендуется проверить выполнение равенства
f1(x*1) + f2(x*2) + f3(x*3) + f4(x*4) = z max
Таблица 2
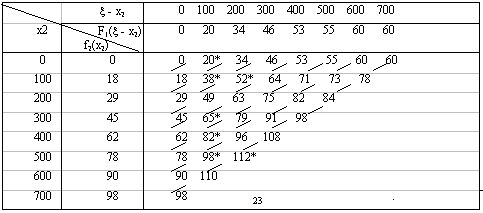
Таблица 3
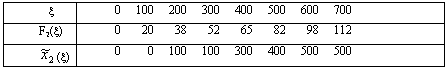
 § 9. Динамическая задача управления производством >и запасами
§ 9. Динамическая задача управления производством >и запасами Предприятие производит партиями некоторые изделия. Предположим, что оно получило заказы на n месяцев. Размеры заказов значительно меняются от месяца к месяцу. Поэтому иногда лучше выполнять одной партией заказы нескольких месяцев, а затем хранить изделия, пока они не потребуются, чем выполнять заказ в тот именно месяц, когда этот заказ должен быть отправлен. Необходимо составить план производства на указанные n месяцев с учетом затрат на производство и хранение изделий. Обозначим:
xj - число изделий, производимых в j -й месяц;
yj - величина запаса к началу j го месяца (это число не содержит изделий, произведенных в j -м месяце);
dj - число изделий, которые должны быть отгружены в j -й месяц;
fj (xj,yj+1) - затраты на хранение и производство изделий в j -м месяце.
Будем считать, что величины запасов к началу первого месяца y1 и к концу последнего yn+1 заданы.
Задача состоит в том, чтобы найти план производства
(x1, x2, ..., xn)(1)
компоненты которого удовлетворяют условиям материального баланса
xj + yj - dj = yj+1j = 1,n(2)
и минимизируют суммарные затраты за весь планируемый период
![]() (3)
(3)
причем по смыслу задачи
xj ³ 0, yj ³ 0, j = 1,n(4)
Прежде чем приступить к решению поставленной задачи, заметим, что для любого месяца j величина yj+1 запаса к концу месяца должна удовлетворять ограничениям
0 £ yj+1 £ dj+1 + dj+2 + ... + dn(5)
т.е. объем производимой продукции xj на этапе j может быть настолько велик, что запас yj+1 удовлетворяет спрос на всех последующих этапах, но не
имеет смысла иметь yj+1 больше суммарного спроса на всех последующих этапах. Кроме того, из соотношений (2) и (4) непосредственно следует, что переменная xj должна удовлетворять ограничениям
Похожие работы
... . Кроме прочего, подобный факультатив может, по-видимому, частично решить две другие очевидные проблемы военного образования: - во-первых, он в состоянии взять на себя функции задачно-методического "мостика" между математикой и специальными дисциплинами (в инженерных вузах подобный мостик достаточно эффективно реализуется общепрофессиональными дисциплинами); - во-вторых - это потенциально главная ...
задача на нахождение условного экстремума. Для ее решения систему неравенств (1) при помощи дополнительных неизвестных х5, х6, х7 заменим системой линейных алгебраических уравнений 4х1+0х2+8х3+7х4+х5=316 (I) 3х1+2х2+5х3+ х4+х6=216 (II) (3) 5х1+6х2+3х3+2х4+х7=199 (III) где дополнительные переменные имеют смысл остатков ...
... ≤7800. Имеем 5х1+9х2 ≤ 7710 9х1+7х2 ≤ 8910 3х1+10х2 ≤ 7800 где по смыслу задачи х1≥0, х2≥0. Получена задача на нахождение условного экстремума. Для ее решения систему неравенств при помощи дополнительных неизвестных х3, х4, х5 заменим системой линейных алгебраических уравнений 5х1+9х2+х3 = 7710 ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
0 комментариев