£ x2 £ 4

0 £ x2 £ 4,

т.е. переменная х2 может принимать значения: 0, 1, 2, 3, 4, а каждому значению х2 отвечает определенное значение у2, вычисляемое по формуле (40):

у2 = 4 - х2

Последовательно находим:

если x2 = 0, то y2 = 4-0 = 4,W 2 (0,2) = 02 + 5× 0 + 2 + 3× 2 + F1(4) = 8 + 56 = 64,

x2 = 1, y2 = 4-1 = 3, W 2 (1,2) = 12 + 5× 1 + 2 + 3× 2 + F1(3) = 14 + 41 = 55,

x2 = 2, y2 = 4-2 =2, W 2 (2,2) = 22 + 5× 2 + 2 + 3× 2 + F1(2) = 22 + 28 = 50,

x2 = 3, y2 = 4-3 = 1, W 2 (3,2) = 32 + 5× 3 + 2 + 3× 2 + F1(1) = 32 + 17 = 49*,

x2 = 4, y2 = 4-4 = 0, W 2 (3,2) = 42 + 5× 4 + 2 + 3× 2 + F1(0) = 44 + 8 = 52.

Наименьшее из полученных значений W 2 есть F2 (2), т.е.

 

причем минимум достигается при значении х2, равном

` 2 (x = y3 = 2) = 3

Аналогично для значения параметра x = у3 = 3, проведя необходимые вычисления, найдем

F2 (x = y3 = 3) = 63;` 2 (x = y3 = 3) = 3.

Процесс табулирования функции F2 (x = y3) приведен в табл. 2, а результаты табулирования сведены в табл. 3.

Таблица 3

x = у3	0	1	2	3	4
F2 (x = y3)	24	36	49	63	78
(x = y3)	2	2	3	3	4

Переходим к следующему этапу. Полагаем k=3 и табулируем функцию F3 (x = y4):

Вычисляем значение функции состояния только для одного значения аргумента x = у4 = 0, так как не хотим оставлять продукцию в запас в конце исследуемого периода. Процесс вычислений приведен в табл. 4. Получаем

причем минимум достигается при двух значениях переменной х3, равных

` 3 (x = y4 = 0) = 3 или ` 3 (x = y4 = 0) = 4.

Таким образом, мы получили не только минимальные общие затраты на производство и хранение продукции, но и последнюю компоненту оптимального решения. Она равна

= 3 или = 4.

Рассмотрим случай, когда на последнем этапе планируем выпускать три единицы продукции

= 3.

Остальные компоненты оптимального решения найдем по обычным правилам метода динамического программирования. Чтобы найти предпоследнюю компоненту, учтем, что

х3 + у3 - d3 = y4

или

3 + у3 - 4 = 0,

откуда

у3 = 1.

Из таблицы (3) значений находим

Аналогично, продолжая двигаться в обратном направлении и учтя, что

х2 + у2 - d2 = y3

			xk	yk = yk+1 + dk - xk	W k(xk, yk+1) =j k(xk) + hkyk+1 + Fk-1(yk)
0 £ y3 £ d3	x = y3	0 £ x2 £ d2 + y3	x2	y2 = y3 + d2 - x2	W 2(x2, y3) = a + bx + c + h2y3 + F1(y2)
0 £ y3 £ 4	x = y3	0 £ x2 £ 2 + y3	x2	y2 = y3 + 3 - x2
	y3 = 0	0 £ x2 £ 2	x2 = 0 x2 = 1 x2 = 2	y2 = 2-0 = 2 y2 = 2- 1 = 1 y2 = 2-2 = 0	W 2(0;0) = 02 + 5× 0 + 2 + 3× 0 + F1(2) =2+28 =30 W 2(1;0) = 12 + 5× 1 + 2 +3× 0 + F1(1)=8+17 =25 W 2(2;0) = 22 +5× 2 + 2 + 3× 0 +F1(0) =16+8=24*
	y3 = 1	0 £ x2 £ 3	x2 = 0 x2 = 1 x2 = 2 x2 = 3	y2 = 3 - 0 = 3 y2 = 3-1 = 2 y2 = 3-2 = 1 y2 = 3-3 = 0	W 2(0;1) = 02 + 5× 0 + 2 + 3× 1 + F1(3) = 5+41=46 W 2(1;1) = 12 + 5× 1 + 2 + 3× 1 + F1(2) =11+28 =39 W 2(2;1) = 22 + 5× 2 + 2 + 3× 1 + F1(1)=19+17 =36* W 2(3;1) = 32 + 5× 3 + 2 + 3× 1 + F1(0)=29+8 =37
	y3 = 2	.......................	........	............................	.............................................................
	y3 = 3	0 £ x2 £ 5	x2 = 0 x2 = 1 x2 = 2 x2 = 3 x2 = 4 x2 = 5	y2 = 5 - 0 = 5 y2 = 5 - 1 = 4 y2 = 5 - 2 = 3 y2 = 5 - 3 = 2 y2 = 5 - 4 = 1 y2 = 5 - 5 = 0	W 2(0;3) = 02 + 5× 0 + 2 + 3× 3 + F1(5) = 11+73=84 W 2(1;3) = 12 + 5× 1 + 2 + 3× 3 + F1(4) =17+56 =73 W 2(2;3) = 22 + 5× 2 + 2 + 3× 3 + F1(3)=25+41 =66 W 2(3;3) = 32 + 5× 3 + 2 + 3× 3 + F1(2)=35+28 =63* W 2(4;3) = 42 + 5× 4 + 2 + 3× 3 + F1(1)=47+17 =64 W 2(5;3) = 52 + 5× 5 + 2 + 3× 3 + F1(0)=61+8 =69
	y3 = 4	0 £ x2 £ 6	x2 = 0 x2 = 1 x2 = 2 x2 = 3 x2 = 4 x2 = 5 x2 = 6	y2 = 6 - 0 = 6 y2 = 6 - 1 = 5 y2 = 6 - 2 = 4 y2 = 6 - 3 = 3 y2 = 6 - 4 = 2 y2 = 6 - 5 = 1 y2 = 6 - 6 = 0	W 2(0;4) = 02 + 5× 0 + 2 + 3× 4 + F1(6) = 14+92=106 W 2(1;4) = 12 + 5× 1 + 2 + 3× 4 + F1(5) =20+73 =93 W 2(2;4) = 22 + 5× 2 + 2 + 3× 4 + F1(4)=28+56 =84 W 2(3;4) = 32 + 5× 3 + 2 + 3× 4 + F1(3)=38+41 =79 W 2(4;4) = 42 + 5× 4 + 2 + 3× 4 + F1(2)=50+28 =78* W 2(5;4) = 52 + 5× 5 + 2 + 3× 4 + F1(1)=64+17 =81 W 2(6;4) = 62 + 5× 6 + 2 + 3× 4 + F1(0)=80+8 =88

			xk	yk = yk+1 + dk - xk	W k(xk, yk+1) = j k(xk) + hkyk+1 + Fk-1(yk)
0 £ y4 £ 0	x = y4	0 £ x3 £ d3 + y4	x3	y3 = y4 + d3 - x3	W 3(x3, y4) = a1+ bx3 + c + h3y4 + F2(y3)
y4 = 0	x = y4	0 £ x3 £ 4	x3	y3 = y4 + 4 - x3
	y4 = 0	0 £ x3 £ 4	x3 = 0 x3 = 1 x3 = 2 x3 = 3 x3 = 4	y3 = 4-0 = 4 y3 = 4- 1 = 3 y3 = 4-2 = 2 y3 = 4-3 = 1 y3 = 4-4 = 0	W 3(0;0) = 02 + 5× 0 + 2 + 2× 0 + F2(4)=2+78=80 W 3(1;0) = 12 + 5× 1 + 2 + 2× 0 + F2(3)=8+63=71 W 3(2;0) = 22 + 5× 2 + 2 + 2× 0 + F2(2)=16+49=65 W 3(3;0) = 32 + 5× 3 + 2 + 2× 0 + F2(1)=26+36=62* W 3(4;0) = 42 + 5× 4 + 2 + 2× 0 + F2(0)=38+24=62*

Самопроверка результатов Таблица 5

Этапы	январь	февраль	март	Итого за 3 месяца
Имеем продукции к началу месяца, шт.	у1 = 2	у2 = 1	у3 = 1	у1 = 2
Производим в течение месяца, шт.	х1 = 2	х2 = 2	х3 = 3	х1+ х2+ х3 = 7
Отпускаем заказчикам, шт.	d1 = 3	d2 = 2	d3 = 4	d1+ d2+ d3 = 9
Остаток к концу месяца (храним в течение текущего месяца), шт.	у2 = 1	у3 = 1	у4 = 0
Затраты на производство, руб.	j (х1)=16	j (х2)=16	j (х3)=26	j (х1) + j (х2) + j (х3) = 58
Затраты на хранение, руб.	h1у2 = 1	h2у3 = 3	0	h1у2 + h2у3 = 4

или

2 + у2 - 2 = 1,

получаем

у2 = 1;

из таблицы (2) значений х1(x ) находим

.

Итак, оптимальный план производства имеет вид

х1 = 2

х2 = 3

х3 = 3,

а минимальные общие затраты составляют 62 единицы.

Полезна самопроверка полученного результата. Для этого по исходным данным и найденному плану производства заполняем таблицу 5 и убеждаемся, что заявки потребителей на каждом этапе выполняются

у1 + х1 ³ d1у2 + х2 ³ d2у3 + х3 ³ d3

2 + 2 ³ 31 + 2 ³ 21 + 3 ³ 4

и что суммарный объем производства и имевшегося к началу первого этапа запаса продукции равен суммарной потребности

у1 + х1 + х2 + х3 = d1 + d2 + d3

2 + 2 + 2 + 3 = 3 + 2 + 4

причем это достигается при наименьших возможных затратах на производство и хранение продукции

j (х1) + j (х2) + j (х3) + h1у2 + h2у3 = F3(y4=0)

16 + 16 + 26 + 1 + 4 = 62

Студенту рекомендуется найти другой вариант оптимальной производственной программы, когда на последнем этапе предполагается произвести 4 единицы продукции, и так же выполнить самопроверку.

§10. Матричная модель производственной программы предприятия

Предприятие состоит из n цехов. Каждый цех выпускает только один вид продукции. Пусть j-й цех выпускает xj единиц продукции, из которых yj единиц отправляет за пределы предприятия как товарную продукцию, а остающаяся часть используется другими цехами предприятия.

Пусть ajk – кол-во продукции j-го цеха, расходуемое на производство единицы продукции k-го цеха. Числа aij образуют матрицу А коэффициентов прямых затрат, называемую структурной. Производственная программа предприятия представляется вектором X(x1, … , xn), а выпуск товарной продукции – вектором У(у1, … , уn). Очевидно,

(Е - А)Х = У или Х = (Е - А)-1У.

Элементы любого столбца матрицы (Е - А)-1, называемой матрицей коэффициентов полных затрат, показывают затраты всех цехов, необходимые для обеспечения выпуска единицы товарного продукта того цеха, номер которого совпадает с номером данного столбца.

При заданном векторе У выпуска товарной продукции легко определить производственную программу Х и наоборот.

Дополним структурную матрицу А матрицей В коэффициентов прямых затрат, получаемых со стороны сырья, полуфабрикатов и т.п. Очевидно, затраты получаемых со стороны материалов определяются элементами матрицы S, где

В = (Е - А)-1У = S

Зная закупочные цены сырья и рыночные цены готовой продукции, можно подсчитать прибыль.

§11. Матричная игра как модель конкуренции и сотрудничества

Пусть игроки – Первый и Второй, играют в матричную игру с матрицей . Пусть стратегия Первого есть , а Второго – . Тогда выигрыш Первого есть случайная величина (с.в.) с рядом распределения:

	a1j		…				…
			…				…

Математическое ожидание этой с.в., т.е. есть средний выигрыш Первого. Пусть есть дисперсия этой с.в. Естественно назвать среднее квадратическое отклонение с.в. , т.е. риском для Первого при игре со стратегиями . Поскольку выигрыш Первого есть проигрыш для Второго, то есть случайный проигрыш Второго и вполне естественно можно назвать риском игры с такими стратегиями и для Второго.

Предположим сначала, что игроки озабочены только максимизацией среднего дохода за партию игры – обычная цель в таких играх. Тогда игроки будут играть со своими оптимальными стратегиями: – Первый игрок и – Второй.

Математическое ожидание с. в. называется ценой игры, обозначим ее .

Но что же назвать риском всей игры?

Вычислим дисперсию выигрыша Первого при оптимальных стратегиях игроков.

.

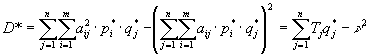Так как , а через сумма обозначена .

Заметим, что в сумме можно оставить лишь те слагаемые, у которых

Заметим теперь, что если Первый играет со стратегией , а Второй отвечает -й чистой стратегией, то выигрыш первого есть с.в. с рядом распределения:

	a1j		…				…
			…				…

Если есть оптимальная стратегия Первого, а , то из теории матричных игр с нулевой суммой известно, что выигрыш Первого при таких стратегиях по-прежнему равен цене игры , а дисперсия выигрыша Первого при этом равна , то есть равна . Таким образом, что происходит с риском выигрыша Первого, можно понять, сравнив дисперсию при оптимальных стратегиях и дисперсию или величины и . Пусть Как легко понять, если среди есть разные числа, то

Теперь можно сделать следующий вывод:

Чуть-чуть отойдя от своей оптимальной стратегии (смотрите ниже Пример) и таким образом почти не уменьшив свой выигрыш, Первый может значительно уменьшить свой риск. При этом уменьшается и риск Второго, что отвечает и его интересам.

Чисто математически можно сказать, что в описанной ситуации риск выигрыша Первого не зависит от его стратегии непрерывно.

Рассмотрим подробно пример матричной игры с матрицей . Как известно, общий случай в окрестности оптимальных стратегий игроков сводится к анализу такой игры.

Пример. Пусть матрица игры есть . Графическое решение этой игры показано на рисунке 1.

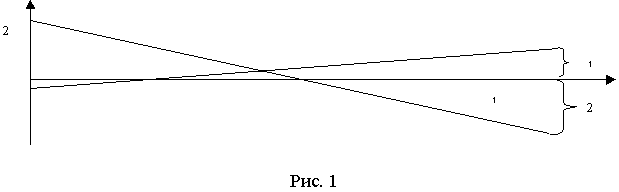
Цена игры , оптимальные стратегии игроков есть , . Дисперсия выигрыша Первого при оптимальных стратегиях , т. е. риск игры равен примерно 1. Далее вычисления дают , ; , Примерная, но достаточно точная зависимость риска Первого в малой окрестности его оптимальной стратегии показана на рис. 2.

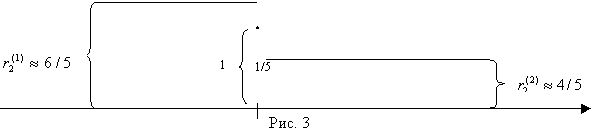
Как видно из рис. 2 при отходе Первого от своей оптимальной стратегии вправо, т. е. при увеличении вероятности x выбора им 1-й строки. Второй начинает отвечать 1-й чистой стратегией и риск Первого скачком увеличивается до , а при отходе Первого от своей оптимальной стратегии влево Второй переходит на свою 2-ю чистую стратегию и риск Первого скачком снижается до

Аналогичное верно и в отношении Второго. Кратко повторим. Примерная, но достаточно точная зависимость риска Второго в малой окрестности его оптимальной стратегии показана на рис. 3. Как видно из рис. 3 при отходе второго от своей оптимальной стратегии вправо, т. е. при увеличении вероятности у выбора им 1-й строки Первый начинает отвечать 2-й чистой стратегией и риск Второго скачком уменьшается до , а при отходе второго от своей оптимальной стратегии влево Первый переходит на свою 1-ю чистую стратегию и риск Второго скачком увеличивается до

Пусть . Эту величину и можно назвать риском всей игры. Однако играть с таким риском можно лишь при согласии обеих сторон. Для анализируемой игры и игроки для достижения такого риска должны играть так: Первый играет со своей оптимальной стратегией 3,5), а Второй должен использовать 2-ю чистую стратегию.

§ 12. Анализ доходности и риска финансовых операций

Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку и цель проведения которой заключается в максимизации дохода - разности между конечной и начальной оценками.

Почти всегда финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль так и убыток (или не очень большая прибыль по сравнению с той, на что надеялись проводившие эту операцию).

Как оценить операцию с точки зрения ее доходности и риска?

Существует несколько разных способов. Наиболее распространенным является представление дохода операции как случайной величины и оценка риска операции как среднего квадратического отклонения этого случайного дохода.

Рассмотрим какую-нибудь операцию, доход которой есть случайная величина Q. Средний ожидаемый доход ` Q - это математическое ожидание с.в. Q: , где pi есть вероятность получить доход qi. А среднее квадратическое отклонение (СКО) - это мера разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Вполне разумно считать s количественной мерой риска операции и обозначить r. Напомним, что дисперсия

D[Q] = M [(Q - ` Q)2] = M [Q2] - ` Q2.

Рассмотрим четыре операции Q1, Q2, Q3, Q,4. Найдем средние ожидаемые доходы ` Qi и риски ri операций.

Ряды распределения, средние ожидаемые доходы и риски:

Q1	:	5	2	8	4	` Q1 = 29/6 » 4.81	r1 » 1.77
		1/2	1/6	1/6	1/6
Q2	:	2	3	4	12	` Q2 = 25/6 » 4.16	r2 » 3.57
		1/2	1/6	1/6	1/6
Q3	:	8	5	3	10	` Q3 = 7	r3 » 2.30
		1/2	1/6	1/6	1/6
Q4	:	1	4	2	8	` Q4 = 17/6 » 2.81	r4 » 2.54
		1/2	1/6	1/6	1/6

Напомним, как находить Q и r.

r1 = M [Q21 ] - (Q1)2; M [Q21] = 25*1/2+4*1/6+64*1/6+16*1/6=159/6;

Q21 = 841/36; D [Q1] = (159*6-841)/36 = 113/36;

Нанесем средние ожидаемые доходы ` Q и риски r на плоскость - доход откладываем по горизонтали, а риски по вертикали (см. рис.):

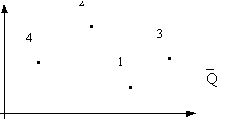
Получили 4 точки. Чем правее точка (` Q, r), тем более доходная операция, чем точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и ниже. Точка (` Q¢ , r¢ ) доминирует точку (` Q, r) если ` Q¢ ³ ` Q и r¢ £ r. В нашем случае 1-я операция доминирует 2-ю, 3-я доминирует 2-ю и 3-я доминирует 4-ю. Но 1-я и 3-я операции несравнимы - доходность 3-й больше, но и риск ее тоже больше.

Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето.

Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар (` Q, r) дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть j (Q)= 2× Q - r . Тогда получаем:

j (Q1)= 2*4.81-1.77 = 7.85; j (Q2)= 4.75; j (Q3)= 11.70; j (Q4)= 3.08

Видно, что 3-я операция - лучшая, а 4-я - худшая.

§ 13. Задача формирования оптимального портфеля ценных бумаг.

На финансовом рынке обращается, как правило, множество ценных бумаг: государственные ценные бумаги, акции частных фирм, векселя и т.п. Ценная бумага удостоверяет возможность получения некоторого дохода. В общем случае владелец получит некоторый случайный доход.

Из характеристик ценных бумаг наиболее значимы две: эффективность и рискованность. Эффективность E есть некоторый обобщенный показатель дохода или прибыли. Будем считать E случайной величиной, ее математическое ожидание есть mЕ.

При исследовании финансового рынка дисперсию обычно называют вариацией V и рискованность обычно отождествляется со Средним Квадратическим Отклонением. Таким образом, V=D[E]= M[( E- mЕ )2 ] и s =.

Рассмотрим общую задачу распределения капитала, который участник рынка хочет потратить на покупку ценных бумаг, по различным видам ценных бумаг.

Пусть xi - доля капитала, потраченная на закупку ценных бумаг i-го вида. Пусть Ei - эффективность (можно считать, доход за некоторый период времени) ценных бумаг i-го вида, стоящих одну денежную единицу. Через Vij будем обозначать ковариацию ценных бумаг i-го и j -го видов (или корреляционный момент Kij). Пусть mi - математическое ожидание эффективности Ei и s i = , где Vii - вариация или дисперсия этой эффективности Ei . Рискованность ценной бумаги i-го вида отождествим со средним квадратическим отклонением s i.

Набор ценных бумаг, находящихся у участника рынка, называется его портфелем. Эффективность портфеля ( в простейшем случае это доход, приносимый ценными бумагами портфеля за какой-нибудь промежуток времени), вообще говоря, есть случайная величина, обозначим ее через Ep, тогда ожидаемое значение этой эффективности mp =M[Ep]=. Дисперсия портфеля есть D[Ep ]= . Величина может быть названа риском портфеля. Обычно D[Ep] обозначается Vp. Итак, мы выразили эффективность и риск портфеля через эффективности составляющих его ценных бумаг и их ковариации.

Каждый владелец портфеля ценных бумаг сталкивается с дилеммой: хочется иметь эффективность побольше, а риск поменьше. Однако поскольку "нельзя поймать двух зайцев сразу", необходимо сделать определенный выбор между эффективностью и риском.

Математическая формализация задачи формирования оптимального портфеля такова:

Найти xi, минимизирующие вариацию эффективности портфеля

Vp = ,

при условии, что обеспечивается заданное значение ожидаемой эффективности портфеля mp, т.е.

mp =.

поскольку xi - доли, то в сумме они должны составлять единицу:

=1 .

Решение (оптимальное) этой задачи обозначим *. Если x*i >0 , то это означает рекомендацию вложить долю x*i наличного капитала в ценные бумаги i-го вида. Если же x*i <0 , то содержательно это означает провести операцию "short sale". Если такие операции невозможны, значит необходимо ввести ограничения xi ³ 0 . Что такое операция "short sale" ?

Если x*i < 0 , то инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги i-го вида (вместе с доходом, какой они бы принесли их владельцу за это время). За это сейчас он получает их денежный эквивалент. На эти деньги он покупает более доходные ценные бумаги и получает по ним доход и оказывается в выигрыше!

Если на рынке есть безрисковые бумаги (к таким можно с некоторой натяжкой отнести государственные ценные бумаги), то решение задачи об оптимальном портфеле сильно упрощается и приобретает замечательное новое качество.

Пусть m0 - эффективность безрисковых бумаг, а x0 - доля капитала в них вложенного. Пусть mr - средняя ожидаемая эффективность и Vr, s r - вариация (дисперсия), СКО эффективности рисковой части портфеля, в рисковую часть портфеля вложено (1-x0) часть всего капитала. Тогда ожидаемая эффективность всего портфеля mp =x0 m0 +(1-x0 )mr, вариация портфеля Vp =(1-x0 )2 Vr и риск портфеля s p =(1-x0 ) s r (считается, что безрисковые бумаги некоррелированы с остальными). Исключая x0, получим

mp = m0 +s p (m -m0 )/ s r ,

т.е. ожидаемая эффективность портфеля линейно зависит от его риска.

Рассмотрим задачу об оптимальном портфеле в этом случае. Рисковые виды ценных бумаг будем нумеровать числами от 1 до n .

x0 m0 + = mp

x0 + = 1

Изложим теперь окончательное решение этой задачи.

Пусть V - матрица ковариаций рисковых видов ценных бумаг, X=(xi), M=(mi) - векторы-столбцы долей xi капитала, вкладываемых в i-й вид рисковых ценных бумаг и ожидаемых эффективностей этого вида, i=1,.., n. Пусть также I - n-мерный вектор-столбец, компоненты которого есть 1. Тогда оптимальное значение долей xi есть

.

Здесь V-1 - матрица, обратная к V . В числителе дроби стоит число, в знаменателе, если выполнить все действия (верхний индекс Т означает транспонирование вектора-столбца), тоже получится число, причем константа, определяемая рынком и не зависящая от инвестора, V-1(M-m0I) - вектор-столбец размерности n . Видно, что этот вектор не зависит от эффективности портфеля mp. Таким образом, вектор долей рисковых видов ценных бумаг пропорциональный этому вектору также не зависит от mp. Следовательно, структура рисковой части портфеля не зависит от mp. Однако сумма компонент вектора X* зависит от mp, именно, компоненты вектора X* пропорционально увеличиваются с ростом mp, поэтому доля x0 безрисковых вложений будет при этом сокращаться.

Пример. Сформировать оптимальный портфель заданной эффективности из трех видов ценных бумаг: безрисковых эффективности 2 и некоррелированных рисковых ожидаемой эффективности 4 и 10 и рисками 2 и 4 . Как устроена рисковая часть оптимального портфеля? При какой ожидаемой эффективности портфеля возникает необходимость в операции "short sale" и с какими ценными бумагами?

Решение. Итак, m0 =2, M=, V=. Зададимся эффективностью портфеля mp. Теперь надо найти обратную матрицу к матрице V . Это просто: V-1 = . Вычислим знаменатель:

.

Итак, вектор долей рисковых бумаг есть X* =((mз-2)/5). Таким образом, рисковые доли должны быть одинаковы и каждая из них равна (mз-2)/10 . Следовательно, x*0 =1-(mр-2)/5 . Понятно, что необходимость в операции "short sale" возникнет, если x*0 < 0, т.е. когда mр > 7 .

Можно доказать, что риск оптимального портфеля в зависимости от его доходности при наличии безрисковых бумаг равен , где

Постановку задачи формирования оптимального портфеля (1) можно словами сформулировать так:

Сформировать портфель минимального риска из всех имеющих эффективность не менее заданной.

Но столь же естественна и задача формирования портфеля максимальной эффективности из всех имеющих риск не более заданного, т.е. найти , максимизирующие ожидаемую эффективность портфеля

при условии, что обеспечивается значение риска портфеля не более заданного, т.е.

поскольку – доли, то в сумме они должны составлять единицу:

Если на рынке есть безрисковые бумаги, то в такой постановке задача формирования такого оптимального портфеля имеет решение, очень похожее на (2): Оптимальное значение долей рисковых бумаг есть

(3)

Можно доказать, что эффективность портфеля максимальной эффективности в зависимости от заданного его риска равна .

§14. Принятие решений в условиях неопределенности

Предположим, что ЛПР (Лицо, Принимающее Решения) рассматривает несколько возможных решений i=1,..m. Ситуация неопределенна, понятно лишь, что наличествует какой-то из вариантов . Если будет принято -e решение, а ситуация есть -я , то фирма, возглавляемая ЛПР, получит доход . Матрица называется матрицей последствий (возможных решений). Какое же решение нужно принять ЛПР? В этой ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но как оценить риск в данной схеме?

Допустим, мы хотим оценить риск, который несет i-e решение. Нам неизвестна реальная ситуация. Но если бы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход. Т.е. если ситуация есть -я , то было бы принято решение, дающее доход .

Значит, принимая -e решение мы рискуем получить не , а только , значит принятие -го решения несет риск недобрать . Матрица называется матрицей рисков.

Пример 1. Пусть матрица последствий есть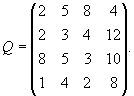

Составим матрицу рисков. Имеем Следовательно, матрица рисков есть

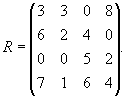
А. Принятие решений в условиях полной неопределенности.

Не все случайное можно "измерить" вероятностью. Неопределенность – более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Кратко говоря, уникальные единичные случайные явления связаны с неопределенностью, массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера.

Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации. Какие же существуют правила-рекомендации по принятию решений в этой ситуации?

Правило Вальда (правило крайнего пессимизма). Рассматривая -e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход .

Но теперь уж выберем решение с наибольшим . Итак, правило Вальда рекомендует принять решение , такое что

Так, в вышеуказанном примере, имеем Теперь из чисел 2,2,3,1 находим максимальное. Это – 3 . Значит, правило Вальда рекомендует принять 3-е решение.

Правило Сэвиджа (правило минимального риска). При применении этого правила анализируется матрица рисков . Рассматривая -e решение будем полагать, что на самом деле складывается ситуация максимального риска

Но теперь уж выберем решение с наименьшим . Итак, правило Сэвиджа рекомендует принять решение , такое что

Так, в вышеуказанном примере, имеем Теперь из чисел 8,6,5,7 находим минимальное. Это – 5. Значит правило Сэвиджа рекомендует принять 3-е решение.

Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение , на котором достигается максимум

где . Значение выбирается из субъективных соображений. Если приближается к 1, то правило Гурвица приближается к правилу Вальда, при приближении к 0, правило Гурвица приближается к правилу "розового оптимизма" (догадайтесь сами, что это значит). В вышеуказанном примере при правило Гурвица рекомендует 2-е решение.

В. Принятие решений в условиях частичной неопределенности.

Предположим, что в рассматриваемой схеме известны вероятности того, что реальная ситуация развивается по варианту . Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил.

Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации -го решения, является случайной величиной с рядом распределения

		…
		…

Математическое ожидание и есть средний ожидаемый доход, обозначаемый также . Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.

Предположим, что в схеме из предыдущего п. вероятности есть (1/2, 1/6, 1/6, 1/6). Тогда

Максимальный средний ожидаемый доход равен 7, соответствует 3-у решению.

Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации -го решения, является случайной величиной с рядом распределения

		…
		…

Математическое ожидание и есть средний ожидаемый риск, обозначаемый также . Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.

Вычислим средние ожидаемые риски при указанных выше вероятностях. Получаем Минимальный средний ожидаемый риск равен 7/6, соответствует 3-у решению.

Нанесем средние ожидаемые доходы и средние ожидаемые риски на плоскость – доход откладываем по вертикали, а риски по горизонтали (см.рис.):

Получили 4 точки. Чем выше точка :, тем более доходная операция, .Q3 чем точка правее – тем более она рисковая. Значит, нужно выбирать точку выше и левее. Точка Q1 доминирует точку , если Q2 и и хотя бы одно из этих .Q4 неравенств строгое. В нашем случае 3-я операция доминирует все остальные.

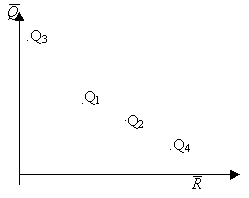
Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбрать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето. В нашем случае, множество Парето, т.е. оптимальных по Парето операций, состоит только из одной 3-й операции.

Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть . Тогда получаем:

. Видно, что 3-я операция – лучшая, а 4-я – худшая.

С. Правило Лапласа.

Иногда в условиях полной неопределенности применяют правило Лапласа равновозможности, когда все вероятности считают равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.

§15. Математико-статистический анализ данных о деятельности производственного экономического объекта

Цель математико-статистического анализа данных, характеризующих поведение исследуемого экономического объекта, состоит в том, чтобы выявить тенденции изменения выпуска продукции и используемых ресурсов, установить зависимость между выпуском и затратами ресурсов и по этим тенденциям и зависимостям найти прогнозы выпуска на ближайшую перспективу.

Выявление тенденций и установление зависимостей между выпуском и ресурсами осуществляется с помощью методов экстраполяции временных рядов и регрессионного анализа, изучаемых в курсе "Теория вероятностей и математическая статистика" [ ].

Расчеты по регрессионным моделям целесообразно выполнять на персональных ЭВМ с помощью пакетов прикладных программ, имеющих в своем составе программы множественной линейной регрессии (например, Statistica for Windows, Statgraf, SAS), однако возможно их выполнение на научном калькуляторе по формулам регрессионного анализа, приведенным в [ ].

Технику проведения расчетов и получения прогнозов покажем на примере исследования экономики США. Исходные данные для расчетов, взятые из следующих источников: Economic Report of the President, 1995,Wash,1995; Statistical Abstract of the USA, 1995, Wash, 1995, приведены в следующей таблице.

Валовой внутренний продукт, (в ценах 1987 г.), основные производственные фонды (в ценах 1987 г.) и число занятых в США в 1960-1995 г.г.

№ п.п.	Год	ВВП (млрд. долл.) Xt	ОПФ (млрд. долл.) Kt	Число занятых (млрд. чел.) Lt
1	1960	1986,9	5596,9	65,8
2	1961	2035,7	5685,6	65,7
3	1962	2140,5	5849,8	66,7
4	1963	2234,2	6098,9	67,8
5	1964	2357,4	6336,1	69,3
6	1965	2493,3	6621,5	71,1
7	1966	2635,7	6921,8	72,9
8	1967	2705,6	7237,0	74,4
9	1968	2816,0	7434,0	75,9
10	1969	2891,0	8062,0	77,9
11	1970	2889,5	8416,8	78,7
12	1971	2978,2	8596,7	79,4
13	1972	3133,2	9533,6	82,2
14	1973	3298,5	9718,1	85,1
15	1974	3283,5	9455,7	86,8
16	1975	3250,2	9493,2	85,8
17	1976	3414,0	9620,9	88,8
18	1977	3568,2	9755,9	92,0
19	1978	3738,8	11217,1	96,0
20	1979	3848,6	12117,0	98,8
21	1980	3824,4	11691,4	99,3
22	1981	3883,1	11987,8	100,4
23	1982	3794,5	10717,1	99,5
24	1983	3938,5	10849,2	100,8
25	1984	4177,5	11989,2	105,0
28	1987	4544,5	13063,7	112,4
29	1988	4724,0	13382,5	115,0
30	1989	4854,2	13838,9	117,3
31	1990	5002,5	15411,8	117,9
32	1991	4881,6	14295,5	116,9
33	1992	4984,1	14252,1	117,6
34	1993	5139,9	14412,5	119,3
35	1994	5372,0	15319,8	123,1
36	1995	5604,1	15939,2	126,7

а) Анализ тенденций изменения и прогнозирование ВВП, ОПФ и числа занятых.

Анализ тенденции изменения и прогнозирование покажем на примере ВВП. Если имеет место линейный тренд, то модель изменения ВВП принимает вид

,

где

- линейный (относительно времени) тренд,

- среднее значение ВВП (значение тренда) при t=0 ( » x1 - ),

- среднегодовой прирост ВВП,

e t – отклонение фактического значения ВВП от тренда.

Оценки коэффициентов тренда приведены в [ ] и имеют вид

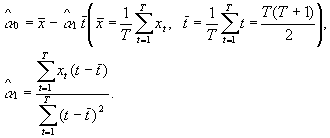
Выполнив расчеты на ЭВМ с помощью указанных ППП, либо непосредственно подставив значения временного ряда ВВП (взятые из таблицы) в последние две формулы, получаем оценки коэффициентов тренда

= 1854,1 – оценка среднего значения ВВП в 1959 г. (млрд. долл.)

= 96,66 – оценка среднегодового прироста ВВП (млрд. долл.), тем самым и оценки тренда

Хt = 1854,1 + 96,66× t.

Прогноз осуществляем по следующей формуле (подставляем будущие значения времени в уравнение тренда)

в частности,

(1996) = 1854,1 + 96,66× 37 = 5430,6;

(1997) = 5527,3;

(1998) = 5623,9.

Точно так же находим оценки трендов и прогнозируемые значения ОПФ и числа занятых

= 5071,7 + 290,05t;

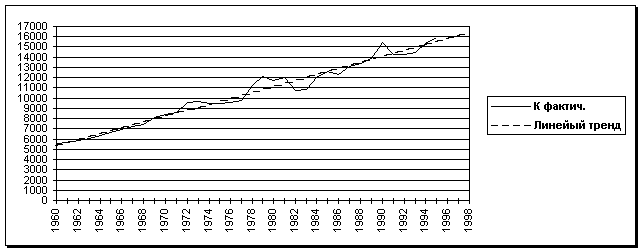
(1996) = 5071,7 + 290,05× 37 = 15803,6;

(1997) = 16093,6;

(1998) = 16383,7;

= 60,36 + 1,796t;

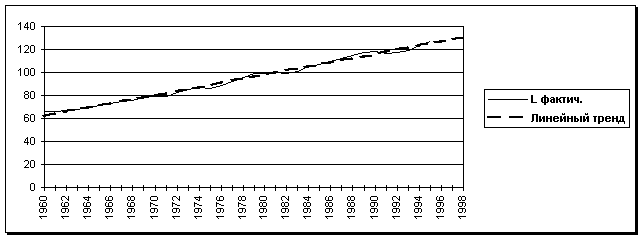
(1996) = 60,36 + 1,796× 37 = 126,8;

(1997) = 128,6;

(1998) = 130,4.

Замечание. Полученные прогнозы основаны на данных 1960 – 1995 г.г. К настоящему времени уже известны фактические данные за 1996 – 1998 г.г., поэтому есть возможность сравнить прогнозируемые значения с фактическими.

На приводимых ниже рисунках показаны фактические, расчетные (по линейному тренду) и прогнозируемые значения.

Прогноз ОПФ на 1996 – 1998 г.г. (млрд. долл.)

Прогноз числа занятых на 1996-1998 г.г. (млн. чел.)

б) Установление зависимости ВВП от ресурсов (ОПФ и числа занятых) и прогнозирование ВВП с помощью найденной зависимости.

Зависимость ВВП от ОПФ и числа занятых постулируем в форме мультипликативной функции

,

где

А – коэффициент нейтрального технического прогресса,

a K, a L – коэффициенты эластичности по фондам и по труду.

При наложении этой гипотетической зависимости на реальные данные приходим к следующей модели

- корректировочный коэффициент, который приводит расчетные (по модели) данные к фактическим.

В логарифмах эта модель приобретает вид уравнения регрессии с двумя независимыми переменными

.

Вводя в программу линейной множественной регрессии в качестве значений зависимой переменной логарифмы ВВП (ln Xt, t = 1,…,T), а в качестве значений двух переменных логарифмы ОПФ (ln Kt, t = 1,…,T) и числа занятых (ln Lt, t = 1,…,T), получаем в результате работы программы оценки параметров регрессии

.

Так расчеты на ЭВМ с помощью ППП " Statistica for Windows" по логарифмам походных данных дали следующие результаты

,

поэтому (= 2,248)

.

Используя прогнозируемые значения ресурсов, получаем прогноз ВВП с помощью найденной зависимости от ресурсов

(1996)

(1997) = 5576,7;

(1998) = 5680,1.

На приводимом ниже рисунке показаны фактические, расчетные (по линейному тренду и по мультипликативной функции) значения ВВП.

Прогноз ВВП на 1996-1998 г.г.(млрд. долл.)

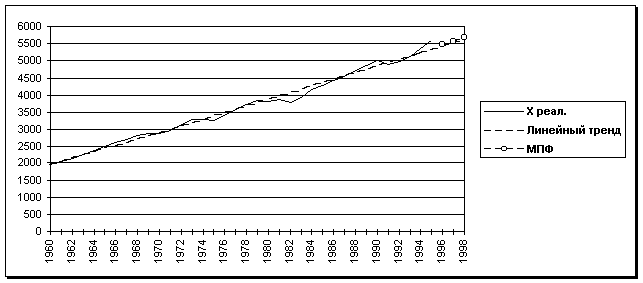
в) Выводы из результатов расчетов.

Как видно из таблицы исходных данных экономика США в 1960-1995 г.г. находилась в состоянии экономического роста, прерываемого в 1960-1961 г.г., 1969-1970 г.г., 1974-1975 г.г., 1980-1982 г.г., 1990-1992 г.г. кризисами и спадами производства.

Этот экономический рост характеризуется среднегодовыми приростами: ВВП – на 96,7 млрд. долл., ОПФ – на 290,1 млрд. долл., числа занятых – на 1,8 млн. чел. Увеличение ОПФ на 1% приводит к увеличению ВВП на 0,404%, а увеличение числа занятых на 1% - на 0,803%, т.е. экономический рост являлся фондосберегающим.

Если бы тенденции сохранились, то к концу 1998 г. ОПФ составили бы 16383,7 млрд. долл. (рост по сравнению с 1995 г. на 2,8%), ВВП достиг бы в 1998 г. значений: при прогнозе по линейному тренду – 5623,9 млрд. долл. (рост на 0,35%), при прогнозе на мультипликативной зависимости – 5680,1 (рост на 1,4%).