Навигация
Непрерывная и дискретная информация
1.2. Непрерывная и дискретная информация.
Чтобы сообщение было передано от источника к получателю, необходима некоторая материальная субстанция – носитель информации. Сообщение, передаваемое с помощью носителя, назовем сигналом. В общем случае сигнал – это изменяющийся во времени физический процесс. Такой процесс может содержать различные характеристики (например, при передаче электрических сигналов могут изменяться напряжение и сила тока). Та из характеристик, которая используется для представления сообщений, называется параметром сигнала.
В случае, когда параметр сигнала принимает последовательное во времени конечное число значений (при этом все они могут быть пронумерованы), сигнал называется дискретным, а сообщение, передаваемое с помощью таких сигналов – дискретным сообщением. Информация, передаваемая источником, в этом случае также называется дискретной. Если же источник вырабатывает непрерывное сообщение (соответственно параметр сигнала – непрерывная функция от времени), соответствующая информация называется непрерывной. Пример дискретного сообщения – процесс чтения книги, информация в которой представлена текстом, т. е. дискретной последовательностью отдельных значков (букв). Примером непрерывного сообщения служит человеческая речь, передаваемая модулированной звуковой волной; параметром сигнала в этом случае служит давление, создаваемое этой волной в точке нахождения приемника – человеческого уха.
Непрерывное сообщение может быть представлено непрерывной функцией, заданной на некотором отрезке [a,b] (рис. 1.2). Непрерывное сообщение можно преобразовать в дискретное (такая процедура называется дискретизацией). Для этого из бесконечного множества значений этой функцией (параметр сигнала) выбирается их определенное число, которое приближенно может характеризовать остальные значения. Один из способов такого выбора состоит в следующем: область определения функции разбивается точками Х1, Х2 … Х на отрезке равной длинны и на каждом из этих отрезков значение функции принимается постоянным и равным, например, среднему значению на этом отрезке; полученная на этом этапе функция называется в математике ступенчатой. Следующий шаг – проецирование значений «ступеней» на ось значений функции (ось координат). Полученная таким образом последовательность значений функции Y1, Y2 … Y является дискретным представлением непрерывной функции, точность которого можно неограниченно улучшать путем уменьшения длин отрезков разбиения области значений аргумента.
Рис. 1.2. Процедура дискретизации непрерывного сообщения.
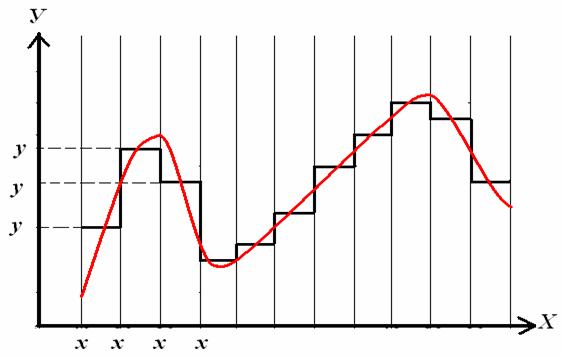
Ось значений функции можно разбить на отрезки с данным шагом и отобразить каждый из выделенных отрезков из области определения функции в соответствующий отрезок из множества значений. В итоге получим конечное множество чисел, определяемых, например, по середине или одной из границ таких отрезков.
Таким образом, любое сообщение может быть представлено как дискретное, иначе говоря, последовательностью знаков некоторого алфавита.
Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер – цифровая машина, т.е. внутреннее представление информации в нем дискретно. Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной для компьютерной обработки.
Существуют и другие вычислительные машины – аналоговые ЭВМ. Они используются обычно для решения задач специального характера и мировой публике практически неизвестны. Эти ЭВМ в принципе не нуждаются в дискретизации входной информации, т.к. ее внутреннее представление у них непрерывно. В этом случае все наоборот – если внешняя информация дискретна, то ее «перед употреблением» необходимо преобразовать в непрерывную.
1.3. Единицы количества информации: вероятностный и объемный подходы.
Определить понятие «количество информации» довольно сложно. В решении этой проблемы существуют 2 основных подхода. Исторически они возникли почти одновременно. В конце 40-ых гг. ХХ века один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.
Вероятностный подход.
Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной кости, имеющей N граней (наиболее распространенным является случай 6-тигранной кости: N=6). Результаты данного опыта могут быть следующие: выпали грани с одним из следующих знаков: 1, 2, …, N.
Введем в рассмотрение численную величину, измеряющую неопределенность – энтропию (обозначим ее Н). Величины N и H связаны между собой некоторой функциональной зависимостью:

(1.1)
А сама функция f является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N=1, 2, …, 6.
Рассмотрим процедуру бросания кости более подробно:
готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность; обозначим ее H1;
кость брошена; информация об исходе данного опыта получена; обозначим количество информации через I;
обозначим неопределенность данного опыта после его осуществления через H2;
За количество информации, которое получено в ходе осуществления опыта, примем разность неопределенностей «до» и «после» опыта:
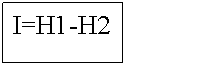
(1.2)
Очевидно, что в случае, когда получен конкретный результат, имевшаяся неопределенность снята (Н2=0), и, таким образом, количество полученной информации совпадает первоначальной энтропией. Иначе говоря, неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта.
Следующим важным моментом является определение вида функции f в формуле (1.1). Если варьировать число граней N и число бросаний кости (обозначим эту величину через М), общее число исходов (векторов длины М, состоящих из знаков 1, 2, …, М) будет равно N в степени М:

(1.3)
Так в случае двух бросаний кости с шестью гранями имеем: Х=62=36. Фактически каждый исход Х есть некоторая пара (Х1;Х2), где Х1 и Х2 – соответственно исходы первого и второго бросаний (общее число таких пар – Х).
Ситуацию с бросанием М раз кости можно рассматривать как некоторую сложную систему, состоящую из независимых друг от друга подсистем – «однократных бросаний кости». Энтропия такой системы в М раз больше, чем энтропия одной системы (так называемый «принцип дитивности энтропии»):
f(6m) = M*f(6)
Данную формулу можно распространить и на случай любого N:
f(Nm) = M*f(N) (1.4)
Прологарифмируем левую и правую части формулы (1.3): lnX=M*lnN, M=lnX/lnN.
Подставляем полученное для М значение в формулу (1.4):
f(X) = lnX/lnM*f(N)
Обозначив через К положительную константу, получим: f(x) = k*lnX, или, с учетом (1.1), H = k*lnX. Обычно принимают k=1/ln2. Таким образом
H =log2N
Это – формула Хартли.
Важным при введении какой – либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, Н будет равно единице при N=2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты, при котором возможны 2 исхода «орел», «решка»). Такая единица количества информации называется «бит».
Все N исходов рассмотренного выше опыта являются равновероятными и поэтому можно считать, что на «долю» каждого исхода приходится одна N-я часть общей неопределенности опыта: (log2N)/N. При этом вероятность 1-го исхода Pi является, очевидно, 1/N.
Таким образом;
H=∑*Pi*log2 (1/Pi)
(1.6)
Так же формула (1.6) принимается за меру энтропии в случае, когда вероятности различных исходов опыта неравновероятны (т.е. Pi могут быть различны). Формула (1.6) называется формулой Шеннона.
В качестве примера определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака «пробел» для разделения слов. По формуле (1.5)
H = log234 ≈ 5 бит
Однако, в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. Ниже приведена таблица 1.1 вероятностей частоты употребления различных знаков русского алфавита, полученная на основе анализа очень больших по объему текстов.
Воспользуемся для подсчета Н формулой (1.6): Н ≈ 4,72 бит. Полученное значение Н, как и можно было предположить, меньше вычисленного ранее. Величина Н, вычисляемая по формуле (1.5), является максимальным количеством информации, которое могло бы приходиться на один знак.
| i | Символ | P(i) | i | Символ | P(i) | i | Символ | P(i) |
| 1 | пробел | 0,175 | 13 | К | 0,028 | 24 | Г | 0,012 |
| 2 | О | 0,090 | 14 | М | 0,026 | 25 | Ч | 0,012 |
| 3 | Е | 0,072 | 15 | Д | 0,025 | 26 | Й | 0,010 |
| 4 | Ё | 0,072 | 16 | П | 0,023 | 27 | Х | 0,009 |
| 5 | А | 0,062 | 17 | У | 0,021 | 28 | Ж | 0,007 |
| 6 | И | 0,062 | 18 | Я | 0,018 | 29 | Ю | 0,006 |
| 7 | Т | 0,053 | 19 | Ы | 0,016 | 30 | Ш | 0,006 |
| 8 | Н | 0,053 | 20 | З | 0,016 | 31 | Ц | 0,004 |
| 9 | С | 0,045 | 21 | Ь | 0,014 | 32 | Щ | 0,003 |
| 10 | Р | 0,040 | 22 | Ъ | 0,014 | 33 | Э | 0,003 |
| 11 | В | 0,038 | 23 | Б | 0,014 | 34 | Ф | 0,002 |
| 12 | Л | 0,035 |
Аналогичные подсчеты Н можно провести и для других языков, например использующих латинский алфавит, - английского, немецкого, французского и др.(26 различных букв и «пробел») по формуле (1.5) получим
H = log227 ≈ 4,76 бит
Как и в случае русского языка, частота появления тех или иных знаков неодинакова.
Если расположить все буквы данных языков в порядке убывания вероятностей, то получим следующие последовательности:
Английский язык «пробел» Е, Т, А, О, N, R,…
Немецкий язык «пробел» Е, N, I, S, T, R,…
Французский язык «пробел» E, S, A, N, I, T,…
Рассмотрим алфавит, состоящий из двух знаков 0 и 1. Если считать, что со знаками 0 и 1 в двоичном алфавите связаны одинаковые вероятности их появления (Р(О) = Р(i) = 0,5), то количество информации на один знак при двоичном кодировании будет равно
H = log22 = 1 бит
Таким образом, количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.
Объемный подход.
В двоичной системе счисления знаки 0 и 1 будем называть битами (от английского выражения Binary digits – двоичные цифры). Отметим, что создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния: некоторый физический элемент, имеющий 2 различных состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий или нет электрический ток; конденсатор, заряженный или незаряженный и т. п. В компьютере бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом, в частности, невозможно нецелое число битов (в отличии от вероятностного подхода).
Для удобства использования введены более крупные, чем бит, единицы количества информации. Так, двоичное слово из восьми знаков содержит один байт информации, 1024 бита образуют килобайт (Кбайт), 1024 килобайта – мегабайт (Мбайт), а 1024 мегабайта – гигабайт (Гбайт).
Между вероятностным и объемным количеством информации соотношение не однозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускают его в объемном. Далее, если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то они не обязательно совпадают, при этом кибернетическое количество информации не может быть больше объемного.
В дальнейшем тексте данного учебника практически всегда количество информации помещается в объемном смысле.
Похожие работы
... и микроэтноэволюцию. Макроэтноэволюция – это эволюция крупных этносов, суперэтносов и макроэтносов, к каковым можно отнести и нации крупных полиэтнических государств. Основными факторами макроэтнических процессов эволюции можно назвать государственно-политическую изоляцию и симпатрическую изоляцию на конфессиональной основе. Географическая изоляция играет значимую роль в макроэтногенезе только на ...
... г., Китай в 1757 г. – просто закрыли свои рынки для европейцев. Тем не менее определенные потрясения испытала экономика почти всех стран Востока, что сказалось и на социальных процессах. Государство везде на Востоке старалось сдерживать рост цен, регулируя их в интересах потребителя, но ничем не стимулируя производителя, что дополнительно замедляло экономическое развитие. Ослабление восточных ...
... большую часть ученых сто лет назад, сегодня трещит по всем швам, не выдерживая потока новых открытий, а также существования других теорий происхождения человека, которые мы рассмотрим ниже. Теория эволюции человека А. Харди Не противоречит теории эволюции, а только слегка заменяет нашего прародителя теория ученного А.Харди, который считает, что человек произошел от водной обезьяны. Главное ...
... в федеральных и республиканских печатных изданиях. Эти типы объединяет авторская обращенность в злобе дня, авторская эмоциональность, глубина постижения сути предмета, многообразие рассуждений и выводов. Глава 2. Телекритика ведущих на страницах российских газет («Известия», «Литературная газета», «Культура») Как известно, в природе не встречается чисто белого цвета, так и в критике авторы не ...
0 комментариев