Параллельность процессов производства также существенно влияет на производительность

3. Параллельность процессов производства также существенно влияет на производительность.

Под принципом параллельности понимается параллельное (одновременное) выполнение отдельных частей (этапов, фаз, операций) производственного процесса, т. е. создание широкого фронта работ по изготовлению детали и сборке РЭА. Чем шире фронт работ, тем меньше при прочих равных условиях длительность производственного цикла.

Унифицированные детали и узлы, входящие во многие РЭА, также могут изготовляться параллельно. При создании конструкции РЭА, который должен быть выпущен в короткий срок, требование к возможности параллельного производства его деталей и узлов является основным.

Параллельность связана с точностью выполнения технологических операций и контролем их результата, главным образом с точки зрения ограниченности времени старения и в связи с этим необходимостью интенсификации процесса. Примером может служить совмещение в одной операции сушки и пропитки обмотки, выполняемых циклически.

Параллельность в организации производственного процесса проявляется в следующих формах.

Параллельность в структуре технологической операции находит свое выражение в многоинструментальной либо многопредметной обработке или сборке.

Параллельность в изготовлении деталей и в их сборке предусматривает одновременное выполнение работ над аналогичными или разными деталями, например при совмещении операций штамповки деталей с их сборкой.

Наибольшими возможностями с технологической точки зрения обладают следующие два вида обеспечения параллельности процессов: 1) изготовление и сборка на многопредметных поточных линиях одновременно нескольких РЭА или их элементов; 2) совмещение на автоматизированных поточных линиях изготовления деталей с их сборкой.

В первом случае за некоторыми рабочими местами на поточной линии можно закрепить операции по нескольким наименованиям изделий, если штучное время по этим операциям значительно меньше соответствующих ритмов выпуска. Естественно, что это требует общности всех или нескольких операций для изготовляемых на поточной линии изделий, т. е. может быть выполнено на основе унификации конструкции различных изделий и типизации процессов изготовления их деталей и сборки. Однако последнее возможно не всегда.

4. При организации производственного процесса в целях увеличения производительности стремятся обеспечить кратчайший путь прохождения изделия по всем фазам и операциям процесса, от запуска исходного материала до выхода готового РЭА. Принцип прямоточности, отвечающий такому построению производственного процесса, может осуществляться как по предприятию в целом, так и в пределах цеха, участка, линии и отдельного рабочего места.

Создание прямоточного производства основано на конструктивных, технологических и организационных предпосылках.

Основным требованием оформления конструкции для обеспечения этого условия является разработка ее элементов таким образом, чтобы деталь или узел могли быть изготовлены в одной фазе производства.

Эти требования могут быть распространены и на аппаратуру, выпускаемую в малых количествах, при условии высокой унификации ее элементов. Детали и элементы массового производства имеют прямоточный технологический маршрут.

Применительно к содержанию технологических операций это говорит о необходимости внедрения методов массового производства в серийное.

5. Под принципом пропорциональности в организации производственного процесса понимается пропорциональная производительность в единицу времени всех производственных подразделений - основных и вспомогательных цехов и обслуживающих хозяйств завода, а в рамках этих цехов и хозяйств - участков и линий, групп оборудования и рабочих мест.

Пропорциональные производственные возможности всех основных цехов завода позволяют считать, что при полном использовании имеющегося оборудования и площадей каждый из цехов и все цехи, вместе взятые, обеспечат равномерный выпуск РЭА, которая по своему номенклатурному составу, количествам и срокам выпуска будет соответствовать требованию комплектного и равномерного выпуска заводом готовой продукции.

Чем более тщательно разработана конструкция РЭА, тем легче обеспечить требования пропорциональности производства. При недостаточной проработанности конструкции отдельные детали или узлы будут «узким местом» в производстве, что потребует непропорционального развития соответствующих рабочих мест, например, по обеспечению стабильности выходных параметров регулировкой.

Хорошими методами улучшения пропорциональности являются повышение расчлененности конструкции и унифицированности ее элементов.

К технологическим методам повышения пропорциональности процессов относятся прежде всего их механизация и автоматизация.

Пропорциональность процесса может быть обеспечена и методами организации производства. К их числу относятся в первую очередь совершенствование производственной структуры цехов и участков (например, создание предметно-замкнутых участков), планирование количества оборудования и его загрузки по сменам, времени запуска в производство и выпуска деталей и узлов.

Обеспечение пропорциональности производства технологическими методами может быть получено в пределах нескольких участков или даже цехов: концентрацией процесса на одном или нескольких рабочих местах, удлинением поточных линий, применением механизированных групповых и типовых процессов.

Пропорциональность производственных процессов должна восстанавливаться все время при последовательном их совершенствовании, связанном с повышением уровня механизации и автоматизации. При этом повышение пропорциональности должно достигаться на основе все более высокой производительности, при экономической эффективности капиталовложений в технологическое оснащение.

6. Устранение или уменьшение всякого рода перерывов в производстве РЭА можно обеспечить путем непрерывности технологических процессов. Устранение межоперационных и внутриоперационных перерывов или их сокращение может быть предусмотрено при разработке конструкций, выполняемых непрерывным производственным процессом (например, применение корпусов, отливаемых под давлением), а также осуществлено технологическими и организационными методами. В поточном производстве, например, за счет синхронизации операций перерывы между ними могут быть сведены к минимуму или ликвидированы.

Применительно к отдельным технологическим операциям принцип непрерывности заключается в перекрытии машинным временем установки и снятия деталей и сборочных элементов, их проверки, а также приемов управления оборудованием.

При производстве РЭА непрерывность процесса повышается как при изготовлении деталей, так и при сборке, а также путем слияния процесса изготовления и сборки.

В сборочных цехах принцип непрерывности процессов при производстве РЭА находится еще (при обычном монтаже) не на достаточно высоком уровне.

Непрерывность процесса повышают также совершенствованием естественных процессов (пропитки, сушки и др.) и, в частности, включением их в поток так же, как операций контроля и испытаний.

Иногда возможно объединение изготовления со сборкой и, в частности, применение автоматизированного оборудования с программным управлением, что делает возможным обеспечить при его перестройке для сборки разных изделий высокую непрерывность процесса.

7. Принцип ритмичности в организации производственного процесса предполагает выпуск в равные промежутки времени одинаковых или возрастающих количеств продукции и соответственно этому повторение через эти промежутки времени производственного процесса во всех его фазах и операциях. Различают ритм выпуска продукции (в конце процесса), операционный (промежуточный) ритм, а также ритм запуска (в начале процесса).

Ритм выпуска может быть длительно устойчивым, если соблюдаются операционные ритмы на всех рабочих местах, выполняющих отдельные операции технологического процесса, т. е. на всех рабочих местах должны комплектно и равномерно повторяться работы, обеспечивающие ритмичный выпуск продукции в заданных номенклатуре и количестве. Операционный ритм может быть обеспечен только при соблюдении ритма запуска.

В сборочных цехах с устойчивой номенклатурой непрерывно выпускаемой" продукции для соблюдения установленного ритма необходимо, чтобы за каждый период ритма на каждой операции выполнялось столько сборочных элементов, сколько необходимо для выпускаемого в течение периода ритма количества годных радиоаппаратов или для обеспечения запланированного выпуска в следующем периоде ритма.

Ритмичность производства в сборочном цехе может быть существенно повышена при разработке групповых и типовых процессов, их унификации и предварительной синхронизации.

Наиболее ритмичной является сборка на одно-предметных поточных линиях, где она может быть основана на дифференцированных, преимущественно ручных операциях или на концентрированных автоматизированных.

158. Методы оптимизации технологических процессов. Перечислите методы и сущность каждого

МЕТОДЫ ОПТИМИЗАЦИИ:

1. Алгоритмические.

2. Градиент.

3. Математическое программирование:

3.1 линейное;

3.2 нелинейное;

3.3 целочисленное;

3.4 динамическое;

3.5 статистическое моделирование.

4. Аналитические (формулы).

Многообразие видов ММ ТС и широкая область их применения отражаются и в различии методов оптимизации. Целью оптимизации является выделение из этого множества единственного варианта ТС, оптимальной по некоторому результирующему критерию или нескольким критериям качества. Сравнение ТС между собой по нескольким критериям качества однозначно можно осуществить с помощью принципа Парето. Согласно этому принципу одна система лучше другой, если соответствующие ей критерии качества имеют значения не хуже критериев качества сравниваемой системы. Причем хотя бы один из них должен быть лучше соответствующего критерия другой системы. Принцип Парето позволяет упорядочить множество рассматриваемых систем и выделить в нем некоторое подмножество, внутри которого сравнение систем по указанному принципу уже невозможно. В тех случаях, когда нецелесообразно сужать поле поиска и вместе с тем необходимо отбросить неоптимальные системы, требуется построение конкретной процедуры реализации принципа Парето. Ее можно сформулировать как задачу оптимизации по одному из критериев качества, когда остальные критерии включены в разряд ограничений.

Выбор единственной оптимальной системы возможен далее только путем введения результирующего критерия, а полученная зависимость может использоваться при этом как дополнительное ограничение. Рассмотренный вариант реализации принципа Парето не является единственным, это задача многокритериальной оптимизации практически сводится к однокритериальной. Поэтому методы однокритериальной оптимизации имеют фундаментальное значение для проблемы оптимизации. Ввиду сложности современных ТС задача полной оптимизации разделяется на ряд подзадач оптимизации. В первую очередь это задачи оптимизации элементов ТС и затем задачи оптимизации всей системы по частным критериям или по некоторому результирующему критерию. Элементы ТС могут быть более или менее детально описаны математически, поэтому их оптимизация может быть осуществлена аналитическими методами. Это в первую очередь метод множителей Лагранжа, метод геометрического программирования, градиентный метод оптимизации.

Градиентный метод оптимизации и его обобщения используют свойство градиента быть направленным в сторону максимального возрастания функции качества. Поэтому если нет ограничений, то алгоритм сводится к генерированию новой точки исходя из предыдущей с помощью следующего соотношения:

,

где - шаг перемещения из  в .

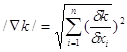
Как видно, перемещение осуществляется из  в  в сторону противоположную направлению градиента. Более сложным обобщением градиентного метода является алгоритм переменной метрики. Однако он требует вычислений разностей градиентов в последовательных точках, т. е. учитывает приращения второго порядка. Аналогичные добавки получаются и в методе сопряженных направлений.

Величина шага  подбирается из условия, чтобы функция имела в следующей точке первый локальный минимум по . При наличии ограничений существует несколько вариантов применения метода градиента: штрафных функций, проекции градиента.

Наиболее наглядным является метод перемещения к седловой точке для функции Лагранжа из некоторой начальной точки (, ).

При переходе к подсистемам более высокого иерархического уровня возможности точного математического моделирования уменьшаются или же точные ММ становятся настолько сложными, что вышеуказанные методы применить нельзя. В настоящее время в связи с широким внедрением средств вычислительной техники получили распространение численные методы оптимизации: метод наискорейшего спуска, метод Ньютона, метод покоординатного спуска, симплекс-метод и др.

Особого упоминания заслуживает метод линейного программирования, поскольку широко используется аппроксимация линейными функциями различных аналитических и экспериментальных зависимостей. Этот метод следует рассматривать не только как метод исследования операций. Существуют его модификации, позволяющие решать задачи параметрического синтеза. Поскольку моделями функционирования большинства ТС являются динамические модели, в которых ТП представляется как некоторый многоэтапный процесс, то наиболее адекватной стратегией их оптимизации является стратегия динамического программирования. Успех применения того или иного метода оптимизации во многом зависит от выбора критерия качества, т. е. аналитической зависимости показателя качества от параметров , по которым оптимизация производится.

Широко используются некоторые унифицированные аналитические зависимости для представления критериев качества, инвариантные относительно метода оптимизации, а между тем выбор подходящей аналитической зависимости для критерия качества позволяет повысить эффективность применяемого метода. Так, при использовании метода Ньютона неравноценны даже эквивалентные с точки зрения описания качества системы функции  и , аналитическая запись которых отличается лишь знаком корня. В частности, для

во втором случае точное решение получается за одну итерацию из любой начальной точки, а в первом случае число итераций зависит от положения начальной точки и может быть значительным.

Исходя из общих особенностей ТС можно дать некоторую схему применения методов оптимизации и используемых при этом критериев. Любая ТС предполагает пространственно-временную организацию перемещения исходных ресурсов (материалов, комплектующих), промежуточных продуктов и законченного изделия. Весьма широкий круг задач подобного рода допускает формулировку в виде задачи линейного программирования. В качестве критериев в данном случае выступают общие затраты на транспортирование, временные затраты, затраты на реконструкцию существующих систем и т. д. Ограничения обычно носят характер неравенств, отражающих возможности средств транспортирования, производительности оборудования, ресурсы поставляемых материалов и комплектующих. Возможности оптимизации систем в целом с помощью метода линейного программирования позволяют на самом раннем этапе ее проектирования просмотреть множество различных ее вариантов и получить весьма полезную дополнительную информацию для ее структурного синтеза. Здесь возможно получение информации об оптимальном размещении системы и рациональном выборе поставщиков и т. д. Следует отметить, что применение линейного программирования не ограничивается оптимизацией ТС, так сказать, в микромасштабе. Имеются весьма важные области применения линейного программирования и для оптимизации ТП. Так, в современной технологии РЭА важную роль играет получение веществ с высокой гомогенностью состава. Задача синтеза таких веществ из исходного сырья, содержащего несколько компонентов, может быть сформулирована как некоторая задача равномерного приближения и решена с помощью метода линейного программирования. Как задача равномерного приближения формулируется также задача построения кинематических узлов с заданными свойствами.

Проектирование элементов ТС предполагает использование преимущественно нелинейных ММ и соответственно методов нелинейного программирования. В качестве обобщенного критерия здесь выступает производительность, надежность при ограничениях на затраты энергии, материалов, комплектующих. Среди указанных методов в настоящее время широкое распространение получил метод геометрического программирования.

Уникальным свойством геометрического программирования является то, что оптимальное значение критерия вычисляется до получения координат оптимальной точки. Это позволяет построить весьма экономичные вычислительные алгоритмы при сравнении различных параметров ТС и облегчить структурный синтез. После проектирования элементов ТС осуществляется возврат к оптимизации системы в целом, но уже преследующий совершенно иные цели, чем при использовании метода линейного программирования. Наиболее важным становится оптимальное распределение функций между отдельными элементами ТС. Математическая модель системы на этом этапе уже известна в наиболее законченном виде. Однако ввиду ее сложности оптимизация на этом этапе встречает трудности вычислительного характера из-за большой размерности задачи. Наиболее важным методом оптимизации на этом этапе является метод динамического программирования.

Использование метода динамического программирования для указанных систем возможно в случае, если критерий качества является аддитивной функцией управляющих переменных, каждая из которых регулирует процесс на определенном этапе. Оптимальное значение управляющей переменной определяется состоянием системы в начале этого этапа и конечной целью управления и не зависит от эволюции системы на предыдущих этапах. Последнее условие соответствует принципу оптимальности Беллмана и является условием применимости динамического программирования. Динамическое программирование не является методом в строгом смысле, а является некоторой общей стратегией, заключающейся в том, что исходная задача становится задачей многоэтапной оптимизации, каждый этап которой, начиная с конечного, использует информацию об оптимальном решении на предыдущем этапе. Эта информация в наиболее явном виде может быть представлена в виде функционального уравнения, связывающего значение критерия качества на оптимизируемом этапе с оптимальным значением критерия качества на предыдущем этапе. Управляющие переменные могут быть векторными величинами.

Другой трудностью использования динамического программирования является то, что функция качества не является выпуклой функцией и поэтому достигаемый этим методом экстремум не является глобальным. Однако примеры решения задач методом динамического программирования показывают, что полученные решения имеют достаточно хорошее качество.

В ряду методов оптимизации ТС заслуживают упоминания метод наискорейшего спуска и метод покоординатного спуска. Особую эффективность эти методы имеют в случае имитационного моделирования ТС, применяемого в том случае, если производные критерия качества по управляющим переменным не могут быть выражены из-за сложности ММ в явном виде через управляющие переменные. Направление наискорейшего спуска оценивается по отклику критерия качества на изменения управляющих переменных. Оба указанных метода являются в настоящее время наиболее универсальными численными методами оптимизации и могут быть реализованы в виде конкретных алгоритмов, позволяющих получить локальные, а в случае выпуклости функции качества и глобальные экстремумы.

Метод случайного поиска может быть применен для оптимизации систем большой сложности и большой размерности (т. е. зависящих от большого числа параметров). Для его реализации необходимы достаточно производительные генераторы случайных (псевдослучайных) чисел.

Все эти методы оптимизации используются также в задачах оптимального управления ТП, в частности в задаче оптимального контроля параметров ТП и качества выпускаемых изделий. Введение развитой системы контроля качества, например, позволяет на ранних стадиях ТП отбраковывать изделия и тем самым устранять затраты на обработку заведомо негодных изделий. Это приводит к задачам линейного и нелинейного, целочисленного программирования. Задача оптимального управления ТП использует сложные динамические модели и требует привлечения самых мощных и универсальных методов оптимизации, среди которых метод случайного поиска зачастую оказывается единственно реализуемым.

Оптимизация современных ТС требует привлечения целого ряда методов оптимизации. Оптимизацию ТС можно рассматривать как некоторый многоэтапный процесс с возможным циклическим повторением этапов. Разработчики ТС должны быть знакомы с широким кругом методов оптимизации, их возможностями и сравнительной эффективностью. Проблема разработки универсального математического и программного обеспечения методов оптимизации для современных ЭВМ в настоящее время, весьма актуальна и далека от разрешения.

Когда имеется одна достаточно четко выраженная цель, степень которой можно оценить на основе одного критерия, используются методы математического программирования. Если эта цель, а следовательно, и степень ее достижения описываются с привлечением методов теории вероятностей или математической статистики, то используется стохастическое программирование.

Для анализа и синтеза ТП сборки и монтажа РЭА, оптимизации их структуры и принципов управления широкое распространение получил метод статистического моделирования. Его сущность состоит в создании специального алгоритма, реализуя который на ЭВМ, можно воспроизвести процесс по элементам с сохранением логической структуры и последовательности протекания процесса.

Метод статистического моделирования включает четыре этапа.

1. Составление содержательного описания процесса. Оно проводится на основе обстоятельного изучения процесса при выполнении натурного эксперимента на реально существующей аппаратуре и оборудовании, а также фиксации количественных характеристик. При отсутствии реального объекта используются накопленный опыт и результаты наблюдений за процессами аналогичного назначения. Содержательное описание позволяет:

- составить ясное представление о физической природе и количественных характеристиках ТП;

- расчленить ТП на ТО и простейшие элементы, определить их показатели и параметры;

- составить схему взаимодействия элементов в операции, а операций в ТП; определить закономерности изменения показателей процесса при изменении его параметров виде таблиц и графиков;

- сформулировать постановку задачи, значение начальных условий.

2. Построение формализованной схемы. На этом этапе уточняются количественные характеристики ТП и дается строгое математическое определение всех зависимостей между показателями и параметрами ТП, его отдельных элементов. Полученные на предыдущем этапе экспериментальные данные подвергаются систематизации с учетом случайного характера их получения. При формализации различают случайные события, случайные величины и случайные функции. Случайные события задаются с помощью вероятностей или частостей их появления, случайные величины- законами распределения или их числовыми характеристиками: средним значением, среднеквадратическим отклонением, корреляционными моментами, а случайные функции - средними значениями и корреляционными функциями. В заключение устанавливается точная математическая формулировка задачи исследований.

3. Составление моделирующего алгоритма проводится на основе построенной ММ. Для преобразования формализованной схемы в ММ необходимо, воспользовавшись готовыми математическими схемами (случайное событие, система массового обслуживания и т. д.), записать в аналитической форме все соотношения, которые еще не были записаны, выразить логические условия в виде систем неравенств, а также придать аналитическую форму всем другим сведениям, имеющимся в формализованной схеме. Числовой материал для удобства обработки на ЭВМ используется не в первоначальном виде, а в форме аппроксимирующих функций.

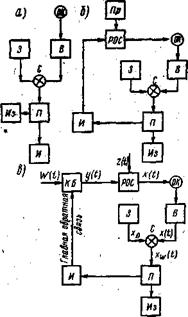
Моделирующие алгоритмы чаще всего представляются в виде схемы, где каждый блок изображает достаточно крупную группу элементов ТП, а связи между блоками отражают логическую структуру ТП. Схема алгоритма не учитывает особенностей системы команд ЭВМ, они вводятся при построении развернутых схем счета и программировании.

4. Разработка методики решения задачи и использование результатов моделирования. Методика решения задачи определяется целью исследования. Количество реализаций процесса моделирования рассчитывается исходя из заданной точности представления результатов. Полученные данные справедливы при фиксированных значениях параметров процесса, входной информации и начальных условиях.

Похожие работы

Автоматика и автоматизация производственных процессов

Скачать

30010

3

0

... Ориентировочный объем раздела КИП и А в дипломном проекте - 10...15 страниц рукописного текста. Графическая часть состоит из одного чертежа - функциональной схемы автоматизации заданного технологического процесса. Подробные указания по выполнению функциональной схемы приведены в разделе 4. 3. УКАЗАНИЯ ПО ВЫБОРУ СРЕДСТВ АВТОМАТИЗАЦИИ Конкретные типы средств автоматизации выбирают с учетом ...

Основы автоматизации производственных процессов

Скачать

25998

0

10

... деталей винта и шайбы. Описан технологический процесс автоматизированного сборочного участка с применением бункерно-загрузочных устройств, ориентируещего приспособления, отсекающих механизмов, транспортеров. СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ.Автоматизация производственных процессов. Шаумян Г.А. ’’ Высшая школа ’’, 1967, -172с. Автоматизация процессов в машиностроении. Учеб. пособие для вузов. ...

По автоматизации производственных процессов

Скачать

20155

3

2

... сопряжения их. Устройства автоматического контроля. Контрольные автоматы классификация по назначению. Разработка новых высокопроизводительных методов и все шире внедряющаяся автоматизация технологических процессов обработки деталей машин привели к существенному снижению трудоемкости их изготовления. Производительность процессов контроля пока растет медленнее. Увеличивается количество ...

Разработка системы автоматизации технологического процесса на примере установки ЭЛОУ-АВТ

Скачать

39590

4

4

... решить только на основе ши­рокого внедрения автоматики в производственные процессы и внедрить автоматизи­рованные системы в различные сферы хозяйственной деятельности, и в первую очередь в проектирование, управление оборудованием и технологическими процессами. Поднять уровень автоматизации производства примерно в 2 раза. Создавать комплексно-автомати­зированные производства, которые можно быстро и ...