Функционирование модели внутренних ресурсов CCF/SSF как системы управления вызовами

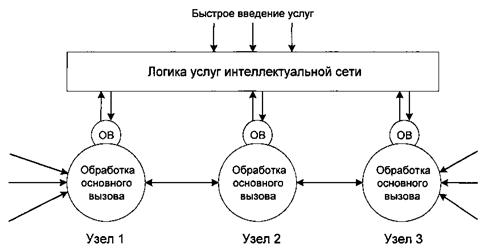
2.4 Функционирование модели внутренних ресурсов CCF/SSF как системы управления вызовами

На основании вышеизложенного, проанализируем последовательность действий, выполняемых объектами модели CCF/SSF.

Пользователь взаимодействует с CCF/SCF через CCAF с целью запросить связь. Менеджер базового процесса обслуживания вызовов (BCM создает BCSM, которая представляет основные функции управления соединением, необходимые для организации и поддержки этой связи. В процессе управления соединением в BCSM отслеживаются события, связанные с обслуживанием вызова.

ВСМ обрабатывает события, происходящие в точках обнаружения в BCSM. В случае если в активизированной точке обнаружения удовлетворяется соответствующий ей критерий, ВСМ информирует FIM/CM о состоянии BCSM и об обнаруженном событии. Если ВСМ нужны инструкции, работа БМСВ приостанавливается в данной DP до их получения. В противном случае BCSM продолжает работать.

Используя полученную от ВСМ информацию, FIM/CM определяет, нужна ли для обработки события логика услуг IN или логика обычных услуг. Кроме того, принимается решение, нужно ли активизировать новую логику услуги, или событие может быть обработано уже активизированной к данному моменту логикой.

Если для обработки события необходимо новое обращение к логике услуг IN, FIM/CM информирует об этом IN-SM и снабжает его информацией о событии и о состоянии BCSM. Если для обработки события необходим запрос обычной услуги (не интеллектуальной), FIM/CM информирует об этом non-IN-SM (менеджера услуг не-IN), который несет ответственность за дальнейшее обслуживание вызова.

IN-SM принимает и обрабатывает информацию о событиях, связанных с услугами IN. Если необходимо новое обращение к логике услуг, IN-SM создает новую IN-SSM, которая представляет состояния соединения в виде, понятном программам логики услуг в SCF. Затем менеджер коммутации услуг формирует и направляет в сторону SCF информационный поток, содержащий сведения о текущем состоянии IN-SSM.

SCF принимает и обрабатывает информационный поток от SSF и активизирует логику затребованной услуги, после чего направляет к SSF ответный информационный поток, содержащий требование к IN-FM изменить состояние IN-SSM таким образом, чтобы был реализован нужный атрибут услуги. SCF может также потребовать от SSF информировать его об определенной группе событий внутри BCSM, то есть указать группу точек EDP которые должны быть активизированы.

IN-SM принимает и обрабатывает информационный поток от SCF с целью изменить должным образом состояние IN-SSM. При этом IN-SM передает соответствующий запрос к FIM/CM, а также следит за изменением состояния IN-SSM с целью обнаружить события, о которых необходимо информировать SCF.

FIM/CM принимает запрос от IN-SM и проверяет его правомерность с учетом того, логика каких услуг к данному моменту активизирована. После этого FIM/CM передает к ВСМ указание, какие функции должны быть выполнены, и требование отслеживать события в BCSM.

Выполняя полученное указание, ВСМ манипулирует состояниями одной или нескольких BCSM. В процессе работы с BCSM он выполняет соответствующие функции управления ресурсами, а также следит за событиями в BCSM. Обнаружив в BCSM событие, ВСМ информирует об этом FIM/CM.

FIM/CM определяет, как следует обрабатывать это событие, после чего сообщает IN-SM, что событие связано с активной в данной момент логикой услуги IN.

IN-SM обрабатывает информацию о событии следующим образом. При условии, что событие связано с активной в данный момент логикой услуги ИС, IN-SM обновляет текущее состояние IN-SSM с тем, чтобы отразить состояние соединения пользователя и передать в информационном потоке от SSF к SCF информацию о событии и о состоянии IN-SSM.

В рассматриваемом нами случае SCF обрабатывает информационный поток следующим образом. При условии, что событие связано с активной логикой услуги IN, содержание информационного потока передается соответствующей программе. Затем формируется ответный информационный поток к SSF, содержащий требование, чтобы IN-SM изменил состояние IN-SSM.

Обмен информационными потоками между SSF и SCF продолжается, пока логика услуги не достигнет завершения (не останется никаких EDP или обслуживание вызова ресурсами CCF/SSF перейдет в область, где, в соответствии с логикой данной услуги, возникновение новых EDP не ожидается).

3. Общий анализ полумарковских процессов, как основы построения базовой модели управления вызова на приемной стороне

3.1 Определения, общая характеристика и основные свойства марковских и полумарковских процессов

Для реализации системы управления вызовами интеллектуальной сети, необходимо рассмотреть организацию базовых моделей управления вызовами на передающей и приемной стороне, в основе которых, как было отмечено, лежит БПОВ. В качестве методики проведения данных исследований предложено использовать аппарат марковских и полумарковских процессов, которые в последнее время достаточно широко используются в теории массового обслуживания, где для исследования реального объекта применяется формальное описание функционирования этого объекта в терминах той или иной системы массового обслуживания (СМО) [16]. Целесообразность применения для исследований марковских и полумарковских процессов объясняется двумя обстоятельствами: во-первых, для марковских процессов хорошо разработан математический аппарат, позволяющий решать многие содержательные физические задачи, и во-вторых, при помощи марковских процессов можно описывать точно или приближенно поведение ряда реальных физических систем и устройств [11].

Приведем общее определение марковского процесса. Случайный процесс  называется марковским, если для любых  моментов времени  из отрезка ,  условная функция распределения «последнего» значения  при фиксированных значениях , , …,  зависит только от , т.е. при заданных значениях     справедливо соотношение

,…,

. (3.1)

Здесь и в дальнейшем через  обозначена вероятность события, указанного в фигурных скобках.

Для трех моментов времени  формула (3.1) принимает вид:

,…,.(3.2)

Поэтому часто говорят, что характерное свойство марковских процессов состоит в следующем: если точно (если настоящее состояние  известно не точно, то будущее состояние марковского процесса будет зависеть от прошлых состояний) известно состояние марковского процесса в настоящий момент времени (), то будущее состояние (при ) не зависит от прошлого состояния (при ).

В случае, если пространство состояний , , …,  марковского процесса  является конечным или счетным, марковский процесс называется цепью Маркова. Если параметр  принимает значения только в дискретном множестве, то цепь Маркова называется цепью с дискретным временем. Если же параметр  принимает значения в некотором непрерывном множестве, то цепь Маркова называется цепью с непрерывным временем.

Важным частным случаем цепи Маркова с непрерывным временем является так называемый процесс гибели и размножения.

Случайный процесс ,  называется процессом гибели и размножения, если он удовлетворяет условиям:

– пространство состояний процесса есть множество неотрицательных целых чисел (или некоторое его подмножество;

– время пребывания процесса в состоянии имеет показательное распределение с параметром  и не зависит от предыдущего поведения процесса;

– после завершения пребывания процесса в состоянии  он переходит в состояние  с вероятностью ,  и в состояние  с вероятностью . Вероятность  полагается равной 1.

Состояние процесса ,  в момент времени  можно трактовать как размер некоторой популяции в этот момент времени. Переход из состояния  в состояние  трактуется как рождение нового члена популяции, а переход в состояние  – как гибель члена популяции. Такая трактовка процесса и объясняет его название.

В дальнейшем применительно к марковским процессам будем пользоваться следующими обозначениями: , если пространство состояний (фазовое пространство) процесса непрерывно, и , если пространство состояний дискретно.

Полумарковские процессы объединяют теорию цепей Маркова, разрывных марковских процессов и теорию восстановления. В соответствии с предложенной методикой анализа марковских процессов приведем определение полумарковского процесса.

Пусть поведение некоторой системы описывается следующим образом. В каждый момент времени система может находиться в одном из  возможных фазовых состояний , , …, , причем известны начальное состояние системы (в начальный момент времени  она находиться в состоянии ) и одношаговые вероятности перехода  , , . следовательно, процесс  есть однородная цепь Маркова.

Сопоставим каждому ненулевому элементу  матрицы вероятностей перехода случайную величину  с функцией распределения . В теории массового обслуживания случайную величину  обычно рассматривают как время пребывания системы в состоянии  при условии, что следующим состоянием, в которое перейдет система, будет . При этом величина  считается неотрицательной и непрерывной с плотностью вероятности . При такой интерпретации величину  можно назвать временем ожидания в состоянии  до перехода в .

Представим, что точка, отображающая поведение системы на фазовой плоскости, остается в состоянии  в течении времени , прежде чем она прейдет в  (рис. 3.1). По достижении  «мгновенного» (в соответствии с матрицей вероятностей перехода ) выбирается следующее состояние , и после того как состояние  выбрано, время ожидания в  полагается равным  с функцией распределения  или плотностью вероятности .Этот процесс затем следует неограниченно продолжать, выбирая каждый раз независимо следующее состояние и время ожидания. Если через  обозначить состояние системы, занятое в момент времени . То полученный случайный момент принято называть полумарковским.

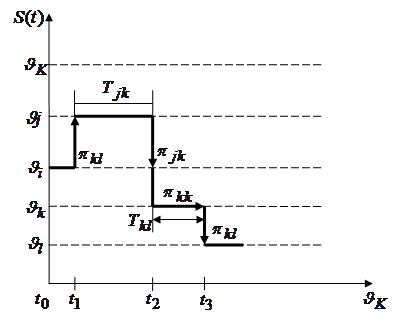Рисунок 3.1– Иллюстрация поведения полумарковского процесса

Из приведенного определения следует, что если игнорировать случайный характер времени ожидания и интересоваться только моментами перехода, то процесс  будет представлять собой однородную цепь Маркова (или вложенным марковским процессом). Однако при учете пребывания процесса в разных состояниях в течении случайного отрезка времени процесс  не будет удовлетворять уравнению Маркова (если не все времена ожидания распределены экспоненциально). Следовательно, процесс является марковским только в моменты перехода. Сказанное оправдывает название «полумарковский процесс» или «полумарковская цепь».

При заданном начальном состоянии дальнейшее поведение полумарковского процесса (полумарковской цепи) полностью определяется матрицей вероятностей перехода , , , и матрицей функций распределения  или (для непрерывных случайных величин ) матрицей плотностей вероятностей  [17].

В рамках исследований полумарковских процессов с позиций теории массового обслуживания наибольший интерес представляет анализ взаимосвязи времени достижения и времени пребывания в состояниях полумарковского процесса. Согласно [16] данный анализ основывается на реализации элементарного процесса чистой гибели. В качестве примера рассмотрим систему , т.е. однолинейную систему массового обслуживания с ожиданием (буфером неограниченной емкости), в которую поступает простейший поток запросов (вызовов) интенсивности , а время обслуживания запросов (вызовов) имеет показательное распределение с параметром .

Исследуя поведение этой системы, можно установить, что случайный процесс  – число вызовов в системе в момент  – является процессом гибели и размножения с вероятностью  равной [16]:

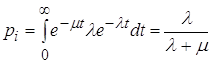, . (3.3)

Анализ данной системы в рамках элементарного процесса чистой гибели основан на исследовании соответствующего графа перехода из одного состояния в другое. Простейший граф перехода имеет вид, показанный на рис. 3.2.

Рисунок 3.2 – Граф переходов элементарного процесса чистой гибели

Обозначим через , , вероятность пребывания процесса в состоянии с номером , а через  функцию распределения времени первого достижения процессом состояния с номером . Тогда между этими функциями можно установить следующие зависимости:

, .

Подставляя эти выражения в условие формировки  получим

. (3.4)

Следовательно, в рассматриваемом элементарном процессе чистой гибели вероятность пребывания процесса в промежуточном состоянии оказывается равной разности функций распределения времени первого попадания процесса в это состояние и времени попадания в следующее состояние. Добавляя и вычитая в правой части уравнения (3.4), затем помножив полученное выражение на   и про интегрировав сначала по  в бесконечных пределах, а затем по частям, получим [18]

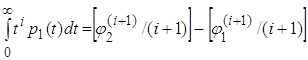, (3.5)

где  – -й начальный момент распределения случайной величины времени попадания процесса в -е состояние . В частности, из формулы (3.5) видно. Что при

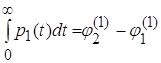. (3.6)

В результате находим, что площадь под кривой  числено равна разности разных средних времен попадания процесса в состояния 2 и 1, а интегральная мера 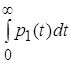 численно равна среднему времени, проведенному процессом в состоянии единицы [18].

Физический смысл полученного результата можно пояснить следующим образом. Обозначим через  случайный момент времени попадания процесса в состояние , а через  длительность пребывания процесса в этом состоянии. Тогда для процесса с графом переходов на рис. 3.2, можно составить следующее уравнение баланса времени:

. (3.7)

Возведя выражение (3.21) в квадрат и применив операцию математического ожидания, учитывая при этом независимость случайных величин  и  получим аналогичное (3.19) выражение для расчета интегральных мер. Так при  находим

.

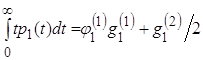Аналогичным образом, возводя уравнение (3.7) в степень  всякий раз будем получать выражения для расчета интегральных мер вида 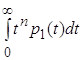 через начальные моменты случайной длительности пребывания процесса в состоянии единицы и первого попадания в нее.

В результате определяется полный набор интегральных мер вида 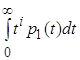 , с помощью которого можно судить о поведении функции .

Похожие работы

Организация интеллектуальной сети в г. Кокшетау на базе платформы оборудования Alcatel S12

Скачать

260457

20

40

... сети телекоммуникаций, а также сравнивая технические возможности оборудований различных фирм в настоящем дипломном проекте предлагаю создать интеллектуальную сеть в г.Кокшетау на базе оборудования S-12 фирмы Alcatel [6]. Выбор оборудования не случаен, так как на сети города полностью эксплуатируется данная система. Это позволяет оптимально решить вопросы по синхронизации, сигнализации и по ...

Система транковой связи LTR

Скачать

58637

0

1

... -систем в единую сеть, но и позволяет предоставить абонентам более широкий набор теле­коммуникационных услуг, включая дуплексную связь. Рис. 5.6. Многозоновая сеть LTR на базе коммутаторов FASTNet, использующая коммутируемые линии ТФОП   5.4. СИСТЕМА MULTI-NET   Состав и структура системы Система Multi-Net предназначена для создания многозоновых сетей связи большой про­тяженности ...

Модернизация сети телекоммуникаций района АТС-38 г. Алматы

Скачать

129463

15

13

... оконечной станции. Спектр линейного сигнала симметричный и достаточно высокочастотный, присутствуют также низкочастотные и постоянная составляющие. Постановка задачи Проведя анализ по модернизации существующих сооружений сети телекоммуникаций района АТС-38, ставим задачу для нашего дипломного проектирования: 1.Увеличить номерную емкость района АТС-38 заменой существующей РАТС типа АТСКУ 10000, ...

Технология размещения базовых станций связи стандарта DCS-1800

Скачать

103375

18

10

... мобильной и фиксированной телефонной связью; в перспективе, не должно быть никакой разницы между мобильным и домашним телефонами. 2. Анализ вопросов проектирования сотовой системы связи стандарта DCS-1800 оператора «Астелит»   2.1 Расчет величины дуплексного разноса между частотными каналами Величина дуплексного разноса определяется соотношением [6]  = - = -, (2.1) где ...