Аналитические решения для простейших полумарковских процессов

3.2 Аналитические решения для простейших полумарковских процессов

Описание поведения систем массового обслуживания с помощью распределений моментов первого, второго и последующих достижений системой того или иного состояния, показанных на примере элементарного процесса чистой гибели, оказывается очень полезным в целом ряде практических исследований. Поэтому целесообразно рассмотреть примеры полумарковских процессов, для которых возможно получение подобных результатов в аналитической форме или в виде эффективных вычислительных процедур.

Для начала рассмотрим простейших процесс, имеющий только два состояния (рис. 3.3). Обозначим через  функцию плотности распределения времени пребывания процесса в состоянии 0, а через  – в состоянии 1.

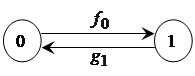
Рисунок 3.3 – Простейший процесс

Соответственно  и  – их преобразования Лапласа. В соответствии с [16], преобразованием Лапласа распределения  будем называть функцию , определяемую как:

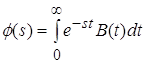. (3.8)

Если  чисто мнимая переменная, преобразование Лапласа совпадает с характеристической функцией . Областью определения функции  обычно считается правая полуплоскость комплексной плоскости. Однако, без существенного ограничения сущности, в рамках проводимого анализа можно рассматривать  как действительное положительное число.

Состояние процесса, приведенного на рис. 3.3 опишем с помощью функции распределения момента -го попадания процесса  в -ю  вершину: 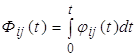. Тогда, учитывая независимость времен пребывания процесса в вершинах 0 и 1, рассматриваемая последовательность переходов будет иметь вид

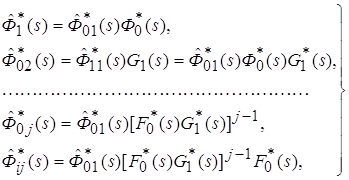, (3.9)

где  – преобразование Лапласа функции .

На основании этих соотношений находят разнообразные характеристики процесса. Так вероятность пребывания процесса в нулевой вершине может быть определена из условия

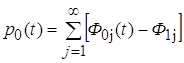. (3.10)

Применяя к выражению (3.10) преобразование Лапласа и используя формулы (3.9), получаем

. (3.11)

Если в момент  процесс находится в нулевой вершине, то  и формула (3.11) принимает вид

. (3.12)

Определение разложения в ряд функции  делает удобным оценку переходного режима.

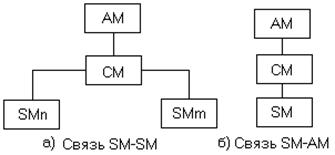
Увеличим число вершин графа на единицу (рис. 3.4.). Заметим, что в этом случае процесс блужданий относительно нулевой вершины может быть описан с помощью некоторого эквивалентного процесса, соответствующего переходам на вспомогательном графе изображенном на рисунке 3.5а.

Рисунок 3.4 – Полумарковский процесс с трема состояниями

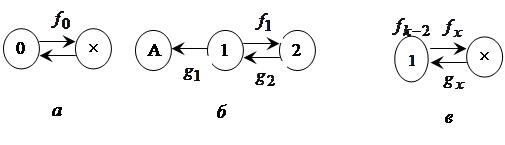
Рисунок 3.5 – Эквивалентные графы для исследования: а) блужданий относительно нулевого состояния; б) возврата в нулевое состояния; в) блужданий относительно промежуточного состояния

Обозначим через  плотность вероятности времени первого перехода процесса из группы состояний {1,2} в нулевое состояние при начале блужданий из состояний 1. Тогда

. (3.13)

Определим функцию . Для этого воспользуемся формулами (3.12), записанными для графа, изображенного на рисунке 3.5б:

;

, ,

где ,  – преобразования Лапласа дефектных случайных величин времени, проводимого процессом в состоянии 1 перед переходом соответственно в состоянии 0 и 2.

С помощью последних выражений находим преобразование Лапласа распределения времени первого попадания процесса в состояние А для графа, изображенного на рис 3.5б

.

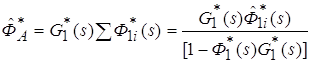Состояние  в общем случае описывается уравнением вида

, (3.14)

где  – некоторый линейный оператор.

Это уравнение описывает еще одно общее и важное свойство марковских процессов, для которых эволюция вероятности перехода . Заметим, что это свойство позволяет исследовать поведение марковских процессов при помощи хорошо разработанных методов решения соответствующих дифференциальных уравнений.

Отсюда, учитывая, что начальные условия для рассматриваемого случая , получаем

.

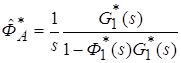Теперь из условия  находим необходимую функцию

. (3.15)

Подставляя выражение (3.15) в формулу (3.13), получаем преобразование Лапласа вероятности пребывания процесса в нулевом состоянии

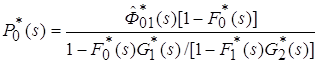. (3.16)

Для определения функции  рассмотрим блуждания относительно первого состояния и построим для них эквивалентный граф (рис. 3.5в). Здесь преобразования Лапласа времени пребывания в состоянии 1 и вне этого состояния определяется из соотношений

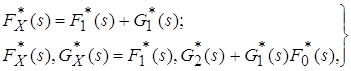, (3.17)

полученных из условия равенства распределений времени пребывания процесса в состоянии 1 и времени возврата в это состояние для исходного графа (рис. 3.4) и эквивалентного (рис. 3.5в). Разрешая систему уравнений (3.17) относительно неизвестных функций, находим

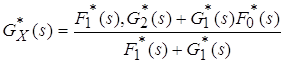. (3.18)

Теперь на основе формулы (3.13), учитывая совпадения форм графов, изображенных на рисунке 3.8, а и б, и используя (3.18), находим преобразование Лапласа вероятности пребывания процесса в состоянии 1

, (3.19)

где .

Функция  в данном случае может быть найдена из условия нормировки . Расположения изображений  в ряды по степеням  для оценки переходных режимов находим путем применения в формулах (3.16) и (3.19) правил операций над рядами по известных разложениям   и  .

Дальнейшее обобщение рассматриваемого класса полумарковских процессов проведем на случай однородных блужданий на неограниченном графе переходов, изображенном на рис. 3.6, где ; , т.е.  и  – функция плотности дефектных случайных величин времени, проведенного процессом в состоянии  перед переходом соответственно в состояния  и .

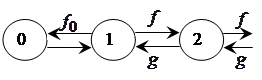
Рисунок 3.6 – Однородный полумарковский процесс

Здесь блуждания относительно крайнего левого нулевого состояния можно представить с помощью двух эквивалентных графов переходов, изображенных на рис. 3.7.

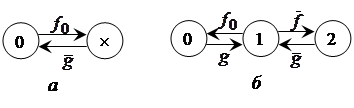
Рисунок 3.7 – Эквивалентные графы для исследования блужданий относительно нулевого (а) и первого (б) состояний

Функции  на обоих эквивалентных графах совпадают, так как представляют собой плотности распределения момента первого возврата из множества вершин графов, полученных из исходного путем отбрасывания собственно нулевой (рис. 3.7а), а также нулевой и первой (рис. 3.7б) вершин. Эти отбрасываемые множества и законы распределений, определяющие блуждание на них, совпадут друг с другом, так как нумерация вершин несущественна. Поэтому установим соответствие между эквивалентными графами и, воспользовавшись выражением (3.15), в которое вместо функции  подставим  получим уравнение относительно неизвестной функции

.

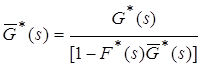Учитывая предельное свойство преобразование Лапласа , решение этого уравнения получаем в виде

. (3.20)

Из выражения (3.20) следует, что вероятность возврата процесса в исходное нулевое состояние для бесконечного графа, изображенного на рис. 3.6, определяется соотношением

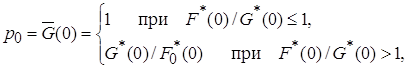
где  и  – вероятности перехода процесса из состояния  ( соответственно в состояния  и . Т.е. соответствуют описанному выше для системы  процессу гибели и размножения.

Отметим, что среднее число возвратов процесса в исходное состояние может быть найдено по формуле .

На основе полученных моделей объединяющих вероятности переходов между состояниями, случайные времена переходов удобно определять по вероятностно – временному графу, который описывает переходы процесса из одного состояния в другое. Такой вероятностно-временной граф для базовой модели управления вызовами на приемной стороне строится на основании соответствующей базовой модели состояний вызова, описанной в предыдущем разделе. Поэтому далее разрабатывается алгоритм функционирования базовой модели управления вызовами на приемной стороне, который определяет последовательность процедур в определенной временной последовательности. Эти процедуры в свою очередь определяют вероятностно-временные характеристиками, для анализа которых и используются вероятностно-временные графы.

Похожие работы

Организация интеллектуальной сети в г. Кокшетау на базе платформы оборудования Alcatel S12

Скачать

260457

20

40

... сети телекоммуникаций, а также сравнивая технические возможности оборудований различных фирм в настоящем дипломном проекте предлагаю создать интеллектуальную сеть в г.Кокшетау на базе оборудования S-12 фирмы Alcatel [6]. Выбор оборудования не случаен, так как на сети города полностью эксплуатируется данная система. Это позволяет оптимально решить вопросы по синхронизации, сигнализации и по ...

Система транковой связи LTR

Скачать

58637

0

1

... -систем в единую сеть, но и позволяет предоставить абонентам более широкий набор теле­коммуникационных услуг, включая дуплексную связь. Рис. 5.6. Многозоновая сеть LTR на базе коммутаторов FASTNet, использующая коммутируемые линии ТФОП   5.4. СИСТЕМА MULTI-NET   Состав и структура системы Система Multi-Net предназначена для создания многозоновых сетей связи большой про­тяженности ...

Модернизация сети телекоммуникаций района АТС-38 г. Алматы

Скачать

129463

15

13

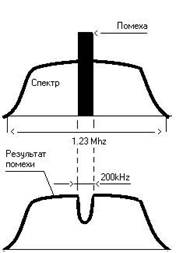
... оконечной станции. Спектр линейного сигнала симметричный и достаточно высокочастотный, присутствуют также низкочастотные и постоянная составляющие. Постановка задачи Проведя анализ по модернизации существующих сооружений сети телекоммуникаций района АТС-38, ставим задачу для нашего дипломного проектирования: 1.Увеличить номерную емкость района АТС-38 заменой существующей РАТС типа АТСКУ 10000, ...

Технология размещения базовых станций связи стандарта DCS-1800

Скачать

103375

18

10

... мобильной и фиксированной телефонной связью; в перспективе, не должно быть никакой разницы между мобильным и домашним телефонами. 2. Анализ вопросов проектирования сотовой системы связи стандарта DCS-1800 оператора «Астелит»   2.1 Расчет величины дуплексного разноса между частотными каналами Величина дуплексного разноса определяется соотношением [6]  = - = -, (2.1) где ...