Обслуживание абонента сетью
Стандарт DECT для связи
Стандарты Bluetooth, Wi-Fi (802.11, 802.16)
Системы сложных сигналов для телекоммуникационных систем
Последовательность прямоугольных импульсов
Производные системы сигналов
Методы фазовой манипуляции сигналов (ФМ2, ФМ4, ОФМ)
Модуляция с минимальным частотным сдвигом
Реализация квадратурных модемов
Характеристики приема сигналов в телекоммуникационных системах
Вероятности ошибок различения M флуктуирующих сигналов
Расчет ошибок различения M сигналов с неизвестными неэнергетическими параметрами
Сравнение синхронных и асинхронных систем связи
Навигация
Системы сложных сигналов для телекоммуникационных систем
Беспроводные телекоммуникационные системы
109728
знаков
0
таблиц
55
изображений
2. Системы сложных сигналов для телекоммуникационных систем
2.1 Спектры сигналов
Спектр сигнала s(t) определяется преобразованием Фурье
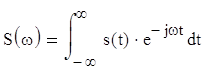
В общем случае спектр является комплексной функцией частоты ω. Спектр может быть представлен в виде
,
где |S(ω)| – амплитудный, а φ(ω) – фазовый спектр сигнала s(t).
Спектр сигнала обладает следующими свойствами:
1. Линейность: если имеется совокупность сигналов s1(t), s2(t), …, причем s1(t)
S1(ω), s2(t)S2(ω), …, то сумма сигналов преобразуется по Фурье следующим образом:
,
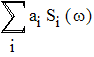где ai – произвольные числовые коэффициенты.
2. Если сигналу s(t) соответствует спектр S(ω), то такому же сигналу, смещенному на t0, соответствует спектр S(ω) умноженный на e-jωt0 s(t-t0)S(ω)e-jωt0.
3. Если s(t)S(ω), то
4. Если s(t)S(ω) и f(t)=ds/dt, то f(t)F(ω)=jωS(ω).
5. Если s(t)S(ω) и g(t)=∫s(t)dt, то g(t)G(ω)=S(ω)/jω.
6. Если u(t)U(ω), v(t)V(ω) и s(t)=u(t)v(t), то
.
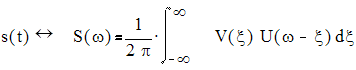Сигнал находится по спектру с помощью обратного преобразования Фурье
.[4]
Рассмотрим спектры некоторых сигналов.
1. Прямоугольный импульс.
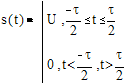
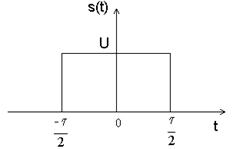
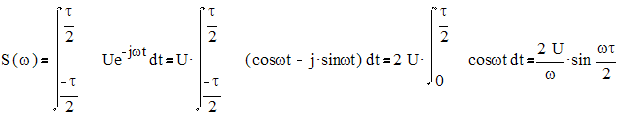
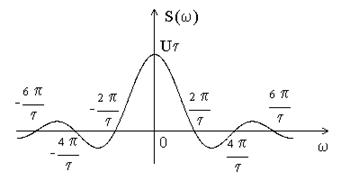
Рис.2.1. Спектр прямоугольного импульса.
2. Гауссовский импульс.
s(t)=Uexp(-βt2)
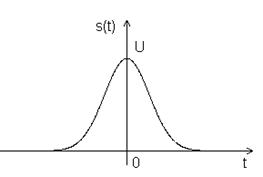
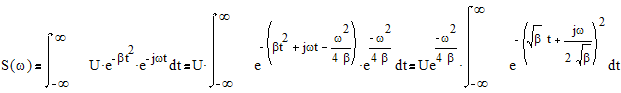
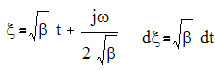
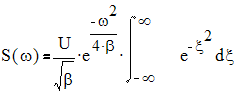
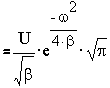
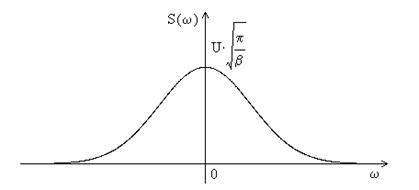
Рис.2.2. Спектр гауссовского импульса.
3. Сглаженный импульс
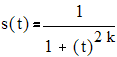
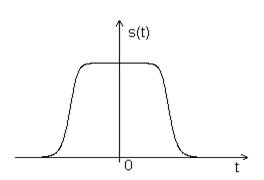
С помощью численного интегрирования находим спектр S(ω).
S(0)=2.052 S(6)=-0.056
S(1)=1.66 S(7)=0.057
S(2)=0.803 S(8)=0.072
S(3)= 0.06 S(9)=0.033
S(4)=-0.259 S(10)=-0.0072
S(5)=-0.221 S(ω)=S(-ω)
Рис. 2.3. Спектр сглаженного импульса.
2.2 Корреляционные свойства сигналов
Для сравнения сигналов, сдвинутых во времени, вводят автокорреляционную функцию (АКФ) сигнала. Она количественно определяет степень отличия сигнала u(t) и его смещенной во времени копии u(t - τ) и равна скалярному произведению сигнала и копии:
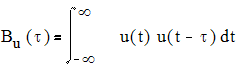
Непосредственно видно, что при τ=0 автокорреляционная функция становится равной энергии сигнала: Bu(0)=Eu.
Автокорреляционная функция четна: Bu(τ)=Bu(-τ).
При любом значении временного сдвига τ модуль АКФ не превосходит энергии сигнала |Вu(τ)|≤Bu(0)=Eu.
АКФ связана со спектром сигнала следующим соотношением:
.
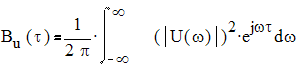Верно и обратное:
.
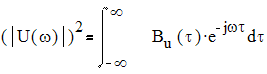Для дискретного сигнала АКФ определяется в следующем виде:
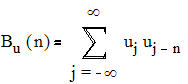
и обладает следующими свойствами.
Дискретная АКФ четна: Bu(n)=Bu(-n).
При нулевом сдвиге АКФ определяет энергию дискретного сигнала:
.
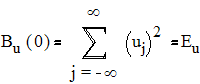Иногда вводят взаимнокорреляционную функцию (ВКФ) сигналов, которая описывает не только сдвиг сигналов друг относительно друга по времени, но и различие в форме сигналов.
ВКФ определяется следующим образом
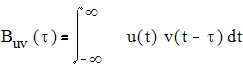
для непрерывных сигналов и
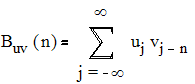
для дискретных сигналов. [4]
Рассмотрим АКФ некоторых сигналов.
Похожие работы
... устройства воздействуют помехи в виде излучений космоса, Солнца, Земли и др. планет. Правильный и точный учет всех особенностей спутниковой связи позволяет выполнить оптимальное проектирование системы связи, обеспечить её надежную работу в наиболее сложных условиях и в то же время исключить излишние энергетические затраты, приводящие к неоправданному усложнению наземной и бортовой аппаратуры. В ...
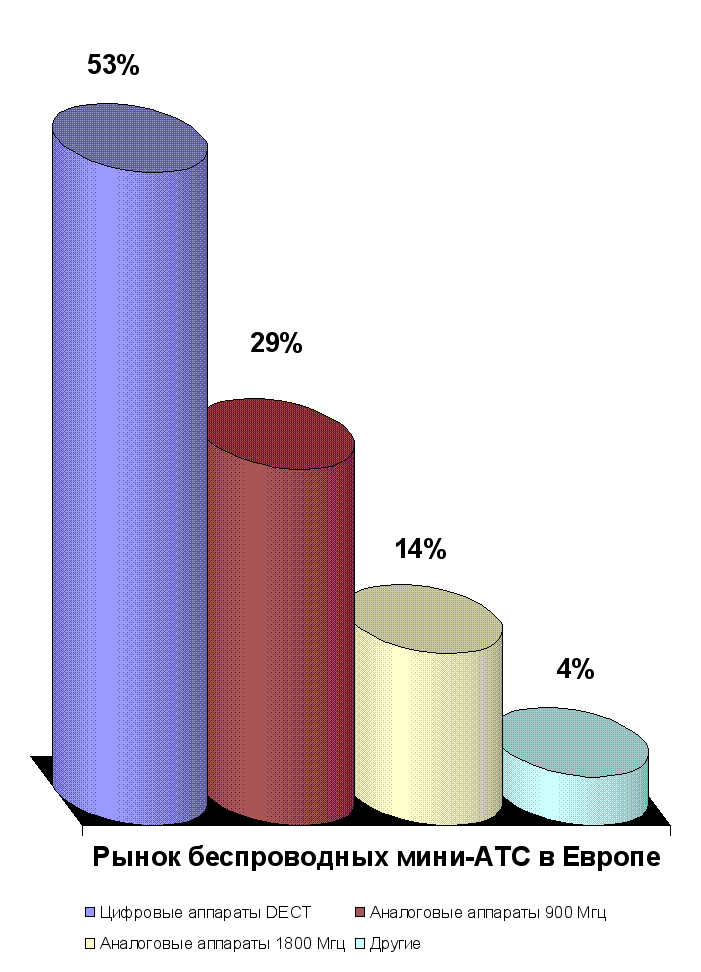
... предприятием аналоговых мини-АТС. ЗАКЛЮЧЕНИЕ В представленной дипломной работе рассмотрена возможность использования мирового опыта по проектированию и строительству офисных телекоммуникационных сетей на базе систем микросотовой связи стандарта DECT фирмой ООО «Сибирь-связь» (г. Красноярск) при оказании услуг по телефонизации офисов. Проведено изучение действующих стандартов используемых при ...
... десять радиоканалов. Исходя, из предполагаемого числа абонентов, определим количество абонентов, приходящихся на одну БС: (2.3) где Nзад – общее число абонентов поселка Омчак Магаданской области; М – общее количество БС. Требуемое число радиоканалов для одной БС: , (2.4) 2.2 Расчет интенсивности нагрузки Интенсивность поступающей нагрузки рассчитывается, исходя из количества ...
... и для шифрования. В WEP применяется алгоритм шифрования RC4. 64-разрядный ключ состоит из 40 разрядов, определяемых пользователем, и 24-разрядного вектора инициализации. Пытаясь повысить безопасность беспроводных сетей, некоторые изготовители оборудования разработали расширенные алгоритмы со 128-разрядными и более длинными ключами WEP, состоящими из 104-разрядной и более длинной пользовательской ...
0 комментариев