Обслуживание абонента сетью
Стандарт DECT для связи
Стандарты Bluetooth, Wi-Fi (802.11, 802.16)
Системы сложных сигналов для телекоммуникационных систем
Последовательность прямоугольных импульсов
Производные системы сигналов
Методы фазовой манипуляции сигналов (ФМ2, ФМ4, ОФМ)
Модуляция с минимальным частотным сдвигом
Реализация квадратурных модемов
Характеристики приема сигналов в телекоммуникационных системах
Вероятности ошибок различения M флуктуирующих сигналов
Расчет ошибок различения M сигналов с неизвестными неэнергетическими параметрами
Сравнение синхронных и асинхронных систем связи
Навигация
Производные системы сигналов
Беспроводные телекоммуникационные системы
109728
знаков
0
таблиц
55
изображений
2.4 Производные системы сигналов
Производным сигналом называется сигнал, который получается в результате перемножения двух сигналов. В случае ФМ сигналов перемножение должно осуществляться поэлементно или, как чаще называют, посимвольно. Система, составленная из производных сигналов, называется производной. Среди производных систем особое значение имеют системы, построенные следующим образом. В качестве основы используется некоторая система сигналов, корреляционные свойства которой не вполне удовлетворяют требованиям к КФ, но которая обладает определенными преимуществами с точки зрения простоты формирования и обработки. Такая система называется исходной. Затем выбирается сигнал, который обладает определенными свойствами. Такой сигнал называется производящим. Умножая производящий сигнал на каждый сигнал исходной системы, получаем производную систему. Производящий сигнал следует выбирать так, чтобы производная система была действительно лучше исходной, т.е. чтобы она обладала хорошими корреляционными свойствами. Комплексная огибающая производного сигнала Sμm(t) равна произведению комплексных огибающих исходных сигналов Um(t) и производящего сигнала Vμ(t), т.е. Sμm(t)= Um(t)Vμ(t). Если индексы изменяются в пределах m=1..M, μ=1..H, то объем производной системы сигналов L=MH.
Выбор производящих сигналов определяется рядом факторов, в том числе и исходной системой. Если сигналы исходной системы широкополосные, то производящий сигнал может быть широкополосным и иметь малые уровни боковых пиков функции неопределенности, близкие к среднеквадратическому значению. Если же сигналы исходной системы узкополосные, то достаточно выполнения неравенства FV>>FU (FV – ширина спектра производящих сигналов, FU – ширина спектра исходных сигналов) и требования малости боковых пиков АКФ.
Возьмем в качестве исходной – систему Уолша. В этом случае производящие сигналы должны быть широкополосными и иметь хорошие АКФ. Кроме того, производящий сигнал должен иметь столько же элементов, что и исходные сигналы, т.е. N=2k элементов, где k – целое число. Этим условиям в целом удовлетворяют нелинейные последовательности. Поскольку основным является требование малости боковых пиков АКФ, то в классе нелинейных последовательностей были отобраны наилучшие сигналы с числом элементов N=16, 32, 64. Эти сигналы показаны на рис. 2.13. На рис. 2.13. указаны также значения числа блоков μ для каждого производящего сигнала. Они близки к оптимальному значению μ0=(N+1)/2. Это и является необходимым условием получения хорошей АКФ с малыми боковыми пиками.
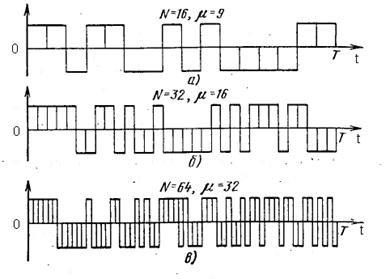
Рис. 2.13. Производящие ФМ сигналы.
Объем производной системы равен объему системы Уолша N. Производные системы обладают лучшими корреляционными свойствами, чем системы Уолша. [6]
3. Модуляция сложных сигналов
3.1 Геометрическое представление сигналов
Рассмотрим геометрическое или векторное представление сигналов. Определим N-мерное ортогональное пространство как пространство, определяемое набором N линейно независимых функций {ψj(t)}, именуемых базисными. Любая функция этого пространства может выражаться через линейную комбинацию базисных функций, которые должны удовлетворять условию
,
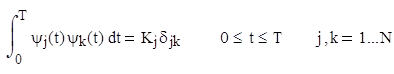где оператор 
называется символом Кронекера. При ненулевых константах Kj пространство именуется ортогональным. Если базисные функции нормированы так, что все Kj=1, пространство называется ортонормированным. Основное условие ортогональности можно сформулировать следующим образом: каждая функция ψj(t) набора базисных функций должна быть независимой от остальных функций набора. Каждая функция ψj(t) не должна интерферировать с другими функциями в процессе обнаружения. С геометрической точки зрения все функции ψj(t) взаимно перпендикулярны.
В ортогональном сигнальном пространстве проще всего определяется Евклидова мера расстояния, используемая в процессе обнаружения. Если волны, переносящие сигналы, не формируют подобного пространства, они могут преобразовываться в линейную комбинацию ортогональных сигналов. Можно показать, что произвольный конечный набор сигналов {si(t)} (i=1…M), где каждый элемент множества физически реализуем и имеет длительность T, можно выразить как линейную комбинацию N ортогональных сигналов ψ1(t), ψ2(t), …, ψN(t), где N
M, так что
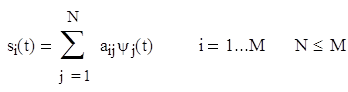где
.
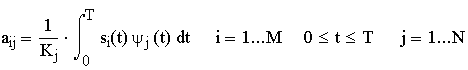Вид базиса {ψj(t)} не задается; эти сигналы выбираются с точки зрения удобства и зависят от формы волн передачи сигналов. Набор таких волн {si(t)} можно рассматривать как набор векторов {si}={ai1, ai2, …,aiN}. Взаимная ориентация векторов сигналов описывает связь между сигналами (относительно их фаз или частот), а амплитуда каждого вектора набора {si} является мерой энергии сигнала, перенесенной в течение времени передачи символа. Вообще, после выбора набора из N ортогональных функций, каждый из переданных сигналов si(t) полностью определяется вектором его коэффициентов si=(ai1, ai2, …,aiN) i=1…M. [2]
Похожие работы
... устройства воздействуют помехи в виде излучений космоса, Солнца, Земли и др. планет. Правильный и точный учет всех особенностей спутниковой связи позволяет выполнить оптимальное проектирование системы связи, обеспечить её надежную работу в наиболее сложных условиях и в то же время исключить излишние энергетические затраты, приводящие к неоправданному усложнению наземной и бортовой аппаратуры. В ...
... предприятием аналоговых мини-АТС. ЗАКЛЮЧЕНИЕ В представленной дипломной работе рассмотрена возможность использования мирового опыта по проектированию и строительству офисных телекоммуникационных сетей на базе систем микросотовой связи стандарта DECT фирмой ООО «Сибирь-связь» (г. Красноярск) при оказании услуг по телефонизации офисов. Проведено изучение действующих стандартов используемых при ...
... десять радиоканалов. Исходя, из предполагаемого числа абонентов, определим количество абонентов, приходящихся на одну БС: (2.3) где Nзад – общее число абонентов поселка Омчак Магаданской области; М – общее количество БС. Требуемое число радиоканалов для одной БС: , (2.4) 2.2 Расчет интенсивности нагрузки Интенсивность поступающей нагрузки рассчитывается, исходя из количества ...
... и для шифрования. В WEP применяется алгоритм шифрования RC4. 64-разрядный ключ состоит из 40 разрядов, определяемых пользователем, и 24-разрядного вектора инициализации. Пытаясь повысить безопасность беспроводных сетей, некоторые изготовители оборудования разработали расширенные алгоритмы со 128-разрядными и более длинными ключами WEP, состоящими из 104-разрядной и более длинной пользовательской ...
0 комментариев