Навигация
ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
1. ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
1.1 Структурный анализ механизма
Подвижно соединенные между собой части механизма называются звеньями. В механизме различают неподвижные и подвижные звенья, которые могут совершать разные типы движений.
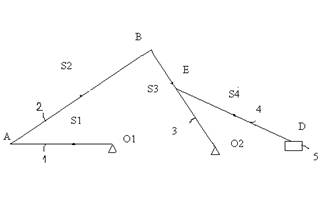
Структурно-кинематической схемой механизма называется условное изображение взаимосвязанных неподвижных звеньев, выполненное в принятом стандартном масштабе длин с принятием условных обозначений кинематических пар.
Определение ступени свободы механизма:
Ступень движения механизма определим по уравнению Чебышева
W = 3n – 2P5 – P4
где n – количество движущихся звеньев механизма;
![]() ,
, ![]() – количество кинематических пар 4-го и 5-го классов.
– количество кинематических пар 4-го и 5-го классов.
Для механизма, что исследуется, количество движущихся звеньев n=4, кинематических пар 5-го класса P5=7 , кинематических пар 4-го класса нет.
Имеем:
W = 3 * 5 – 2 * 7 - 0 = 1
Для работы механизму необходима только одно ведущее звено, так как ступень движимости равна единице.
1.2 Кинематический анализ механизма
1.2.1 Определение скоростей точек и звеньев механизма
Планом скоростей называется диаграмма, на которой изображены векторы скоростей точек плоского механизма.
Для определения скоростей точек и звеньев механизма воспользуемся методом планов скоростей. Скорость точки А (равно, как и скорость точки D) равна нулю, и поэтому построение планов скоростей начинаем со скорости точки B ведущего звена АB (так как можно определить его угловую скорость w и известна длинна данного звена АВ)
Найдем скорость ведущего звена w, беря во внимание, что нам известна частота вращения n; w - обороты в минуту, 1 оборот = 2П, w = ![]() , отсюда:
, отсюда:
w = ![]() 56,52 (об/мин)
56,52 (об/мин)
Учитывая, что скорость ведущего звена w теперь известна, скорость точки B определим из уравнения
VВ = w * LАВ
где LAB – длина звена АB, м.
VB = 56,52 * 0,025 = 1,41 (м/с)
Вектор VB направлен перпендикулярно звену АB.
От произвольно взятой точки Pv (полюса плана скоростей) отложим вектор скорости точки В, перпендикулярен звена АВ и направлен в сторону вращения.
Выбираем масштабный коэффициент скорости m (определим из уравнения):
mV=VB/PVв
где VB – скорость точки, м/с;
PVв– длина вектора, мм.
m= 1,41/97,5= 0,014 (![]() )
)
Определяя скорость точки С будем исходить из того, что эта точка одновременно принадлежит двум звеньям ВС и CD.
Для определения скорости точки C будем использовать теорему о разложении скоростей.
По принадлежности точки C звену ВС записываем первое векторное уравнение:
VС = VВ +VСВ
В этой векторной сумме известно первое слагаемое (из построения графика скорости точки В), а VСВ – только направление (этот вектор перпендикулярен звену СВ). Проводим соответствующую линию на плане скоростей через точку В.
По принадлежности точки C звену СD записываем второе векторное уравнение:
VС = VD+VСD
Из этого уравнения сразу можно выделить, что VD = 0, так как точка D – неподвижна, а про VСD известно лишь то, что этот вектор перпендикулярен ВА. Таким образом мы можем провести вектор, перпендикулярный СD и проходящий через полюс PV, а скорость точки С определяется:
VC = вс * mV = 73 * 0,014
где вс – вектор, взятый из плана скоростей, мм
Для нахождения скорости точки Е необходимо составить пропорцию, из которой мы получим величину отрезка се.
ВС/СЕ = вс/се;
се = СЕ * вс / ВС
так как: ВС = 180 мм; СЕ = 52 мм; вс = 70 мм
се =20,2 мм
Данную полученную величину откладываем на плане скоростей от точки с по продолжению прямой вс. Рассчитываем VE
VE = PVе * mV = 62,5 * 0,014 = 0,966
Определим скорость точки F. Точка F принадлежит звену EF и ползуну 5 (траектория движения ползуна – прямая постоянная горизонтальная линия).
Сложим векторное уравнение:
VF =VE + VFE
В этой векторной сумме известно первое слагаемое, а VFE – только направление (этот вектор перпендикулярен звену EF). Проводим соответствующую линию на плане скоростей через точку е.
Высчитаем скорость точки F как:
VF = PV f * mV = 52 * 0,014 = 0,728
VFE = ef * mV = 32 * 0,014 = 0,448
В данном разделе мы определили Скорости точек и звеньев механизма методом построения планов скоростей, значения которых сведены в таблице 1.1
| Точка | Скорость точки, м/с |
| VА | 0 |
| VВ | 1,4 |
| VС | 0,966 |
| VD | 0 |
| VE | 0,875 |
| VF | 0,728 |
Похожие работы
... Отсюда: H (1.48) Н.м (1.49) Полученные данные занесем в таблицу 1.4. Таблица 1.4 Fур, Н Мур, Н×м 28 0.7 2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими внешними усилиями ...
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
... H 14 23,4 22 R, H 14 24,2 11,8 1 22,2 2. Расчет элементов кинематических пар на прочность. 2.1. Определение внешних сил, действующих на звенья. В результате динамического анализа плоского рычажного механизма определены внешние силы, действующие на звенья и кинематические пары. Такими внешними усилиями являются силы инерции F , моменты инерции M , а также реакции ...
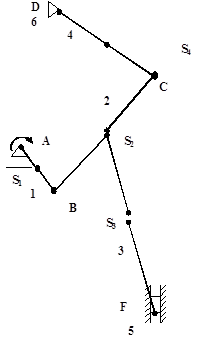

0 комментариев