Навигация
Построение плана ускорений
1.2.2 Построение плана ускорений
Для определения ускорений точек и звеньев механизма воспользуемся методом планов ускорений.
Построению планов ускорений предшествует построение планов скоростей, так как нам понадобятся все значения скоростей (Таблица 1.1)
Ускорение точки имеет 2 составляющих: Нормальную (центростремительную) и касательную (тангенциальную)
Полное ускорение будет суммой этих двух составляющих.
Построение планов ускорений начинаем с точки В ведущего звена механизма АВ (точка А ускорения не имеет). В данном случае есть только нормальная составляющая (из формулы ![]() , где
, где ![]() ) направленная по радиусу вращения к центру вращения (точка А).
) направленная по радиусу вращения к центру вращения (точка А).
Масштабный коэффициент ускорений найдём таким образом:
mа= ![]() = 78,4/98 = 0,8 (
= 78,4/98 = 0,8 (![]() )
)
Где величина Рав длинна первого произвольного вектора в на плане ускорений.
Находим ускорение точки С относительно точки В из уравнения:
![]()

Где при делении на mа мы найдем расстояние в мм, которое следует отложить на плане ускорений. Данный вектор С вокруг В мы переносим параллельно звену ВС на план ускорений из вектора в. Рассмотрим тангенциальное ускорение, оно будет перпендикулярно данному отрезку ![]() .
.
Находим точку С относительно точки D:
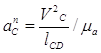 =
=![]()
Полученную в мм величину отложим из полюса Ра параллельно звену CD. Данному вектору построим перпендикуляр этому ветору и на пересечении двух перпендикуляров (данного и перпендикуляра ![]() ) будет точка с, вектор, проведенный из полюса Ра к точке с будет полным ускорением точки с.
) будет точка с, вектор, проведенный из полюса Ра к точке с будет полным ускорением точки с.
Точка е на плане ускорений будет лежать на отрезке вс на некотором расстоянии от точки с, найти которое можно составив пропорцию
ВС/СЕ = вс/се;
се = СЕ * вс / ВС
так как: ВС = 180 мм; СЕ = 52 мм; вс = 50 мм
се = 14,5 мм
Находим ускорение для точки F (ползун) из уравнения:
![]()
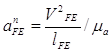 =
=![]()
Данную величину откладываем от точки е параллельно звену FE и строим перпендикулярную тангенциальную составляющею. В точке пресечения с линией траектории движения ползуна F проходящей через полюс Ра зафиксируем точку f, а расстояние Ра f будет ускорением точки F.
Для последующих расчетов нам понадобятся:
![]() СВ = свnс*mа=48,5*0,8=38,8
СВ = свnс*mа=48,5*0,8=38,8
![]() С = сnс*mа=87,5*0,8=70
С = сnс*mа=87,5*0,8=70
![]() FE= ef*mа=28,5*0,8=22,8
FE= ef*mа=28,5*0,8=22,8
|
| 78,4 |
|
| 13 |
|
| 23,33 |
|
| 5,017 |
|
| 38,8 |
|
| 70 |
|
| 22,8 |
А также угловые ускорения:
![]() 0
0
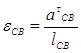 =38,8/0,09=431,11
=38,8/0,09=431,11
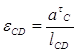 =70/0,05=1400
=70/0,05=1400
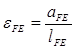 =22,8/0,05=456
=22,8/0,05=456
|
| 0 |
|
| 431,11 |
|
| 1400 |
|
| 450 |
Ускорения центров масс (которые по условию находятся в центре звена) найдем по формуле: aSn = РаSn* mа
mа = 0,8
aS1 = РаS1 * mа = 48,5 * 0,8 = 38,8
aS2 = РаS2 * mа = 90* 0,8 = 72
aS3 = РаS3 * mа =45* 0,8 = 36
aS4 = РаS4 * mа = 44,5* 0,8 = 35,6
aS5 = РаS5 * mа = 43,5 * 0,8 = 34,8
| aS1 | 38,8 |
| aS2 | 72 |
| aS3 | 36 |
| aS4 | 35,6 |
| aS5 | 34,8 |
Имея данные вышеобчисленные величины, находим силы инерции:
![]() = - 4*38,8 = 155,2
= - 4*38,8 = 155,2
![]() = - 15*72 = 1080
= - 15*72 = 1080
![]() = -5*36 = 180
= -5*36 = 180
![]() = - 8*35,6 = 284,8
= - 8*35,6 = 284,8
![]() = - 11*34,8 = 382,8
= - 11*34,8 = 382,8
| -155,5 |
|
| -1080 |
|
| -180 |
|
| -284,8 |
|
| -382,8 |
Похожие работы
... Отсюда: H (1.48) Н.м (1.49) Полученные данные занесем в таблицу 1.4. Таблица 1.4 Fур, Н Мур, Н×м 28 0.7 2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими внешними усилиями ...
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
... H 14 23,4 22 R, H 14 24,2 11,8 1 22,2 2. Расчет элементов кинематических пар на прочность. 2.1. Определение внешних сил, действующих на звенья. В результате динамического анализа плоского рычажного механизма определены внешние силы, действующие на звенья и кинематические пары. Такими внешними усилиями являются силы инерции F , моменты инерции M , а также реакции ...

0 комментариев