Навигация
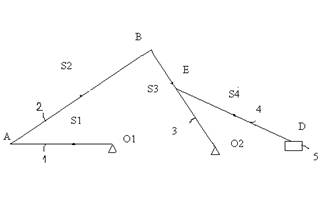
1.3.3 Силовой анализ группы 0-1
Составим уравнение моментов относительно точки А:
![]()
G1 = 39,2
![]() = 1078 H
= 1078 H
Определим Рур:
![]()
Для построения силового многоугольника выберем масштабный коэффициент, составим уравнение и построим силовой многоугольник:
mF = ![]() /PF
/PF![]() =30 (Н/мм)
=30 (Н/мм)
Проведем расчеты и полученные данные внесем в таблицу:
| Сила | Сила, Н | Длинна отрезка, мм |
|
| 155,2 | 5,2 |
| G1 | 39,2 | 1,3 |
| Рур | 2149,73 | 71,65 |
|
| 1078 | 35,9 |
Строим план сил в соответствии с уравнением:
![]() + G1+Рур+
+ G1+Рур+![]() +
+![]()
Соответственно с уравнением и полученными величинами длин построим известные силы (от полюса) ![]() , G1, Рур,
, G1, Рур, ![]() . Замкнем силовой многоугольник, получим вектор
. Замкнем силовой многоугольник, получим вектор ![]() . Далее измеряем длину вектора и переведем ее обратно:
. Далее измеряем длину вектора и переведем ее обратно: ![]() = 79 мм = 2370 Н
= 79 мм = 2370 Н
2. ПРОЕКТНЫЙ РАСЧЕТ ЗВЕНЬЕВ МЕХАНИЗМА НА ПРОЧНОСТЬ
2.1 Выбор расчетной схемы
В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними силами являются силы инерции ![]() , моменты инерции
, моменты инерции ![]() и реакции в кинематических парах R. Под воздействием внешних сил звенья плоского механизма подвергаются деформации изгиба и растяжения (или сжатия)
и реакции в кинематических парах R. Под воздействием внешних сил звенья плоского механизма подвергаются деформации изгиба и растяжения (или сжатия)
Для расчета звена на прочность была выбрана группа 4-5.
Данное звено находится одновременно под воздействием деформации изгиба и растяжения
На стадии проектирования механизму необходимо дать оценку на прочность его элементов. Для этого следует определить с помощью метода сечений величину внутренних усилий, которые действуют в звеньях данного механизма.
2.2 Построение эпюр
Для звена 4-5 (FE) выделим 2 участка: FS4, S4E, в произвольной точке каждого выделенного участка берется сечение с условной длинной Z1 и Z2 соответственно.
Методом сечений рассчитаем Nz:
Nz1 = ![]() + Рп.с = 502,8
+ Рп.с = 502,8
Nz2 = ![]() = 246
= 246
По этим уравнениям строится эпюра Nz
Для поперечной силы Qy также запишем уравнения:
Qy1 = ![]() - G5 = -83,8
- G5 = -83,8
Qy2 = ![]() - G5 +
- G5 + ![]() τ*cosβ - G4 = - 147,7
τ*cosβ - G4 = - 147,7
По данным уравнениям строим эпюры Qy
Для изгибающего момента высчитаем и построим эпюры по следующим уравнениям:
Mx1 = (![]() - G5)*Z 1
- G5)*Z 1
Mx2 = -![]() Z2
Z2
Для первого участка 0 <= Z1 => 0,025, отсюда:
Mx1 (при Z1 = 0) = 0
Mx1 (при Z1 = 0,025) = -2,12
Для второго участка 0 <= Z2 => 0,05, отсюда:
Mx2 (при Z2 = 0) = 0
Mx2 (при Z2 = 0,05) = -3,93
По данным значениям строим эпюры.
2.3 Подбор сечений
Проанализировав все данные эпюры мы находим опасное сечение (в данном случае – опасное сечение проходит через точку S4, в особенности потому что в ней изгибающий момент наибольший:
![]() -1,2
-1,2
Деформация изгибающего момента обуславливает появление в материале нормальное напряжение, которое не должно быть больше допустимого [σ]:
![]()
Это уравнение дает возможность найти геометрические размеры опасного сечения через подбор параметров W.
Проведем расчеты для прямоугольного сечения с параметрами h x b? При этом h = 2b. Тогда:
![]() =
=
Подстановка в уравнение для напряжения дает
![]() ,
,
![]() = 2,5 мм
= 2,5 мм
Тогда:
h=4,4*2 = 8,8(мм)
Для круглого сечения:
![]() .
.
Подстановка в уравнение для напряжения дает
![]() ,
,
![]() = 6,94 мм
= 6,94 мм
Для сложного сечения геометрические параметры найдем подбором. Для этого рассчитаем Wx, приняв за ![]() , по формуле:
, по формуле:
![]() = 32,75 (мм3)
= 32,75 (мм3)
Материал для данного механизма – СТ 3, ![]() .
.
Данному двутавровому сечению соответствует профиль № 10 со следующими параметрами:
h=100 мм, b=70 мм, d=4.5 мм, t=7.2 мм, R=7.0 мм, r=3.0 мм
ВЫВОДЫ
Во время данного учебного курсового проектирования мы на конкретном практическом задании закрепили знания, полученные во время изучения материала курса «Теоретическая и прикладная механика»
Целью проекта было решение поставленной задачи: определение нагруженности плоского рычажного механизма по заданной схеме и исходным характеристическим данным.
Был проведен комплексный динамический и силовой анализ, во время которого выяснили, что механизм состоит из четырех кинематических пар, также были построены планы скоростей, ускорений, а так же планы сил для каждой группы звеньев (согласно разбиению на группы Асура), после чего были определены опасные сечения.
Для определения нагруженности было выбрано звено EF (опасное сечение для данного звена находится в точке S4, согласно построенным эпюрам)
В завершении работы были проведены расчеты определения параметров сечений звена механизма для прямоугольного, круглого и двутаврого сечений.
Похожие работы
... Отсюда: H (1.48) Н.м (1.49) Полученные данные занесем в таблицу 1.4. Таблица 1.4 Fур, Н Мур, Н×м 28 0.7 2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими внешними усилиями ...
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
... H 14 23,4 22 R, H 14 24,2 11,8 1 22,2 2. Расчет элементов кинематических пар на прочность. 2.1. Определение внешних сил, действующих на звенья. В результате динамического анализа плоского рычажного механизма определены внешние силы, действующие на звенья и кинематические пары. Такими внешними усилиями являются силы инерции F , моменты инерции M , а также реакции ...
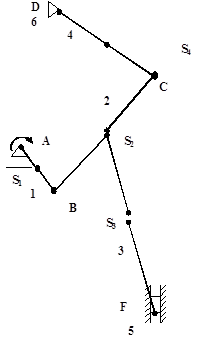

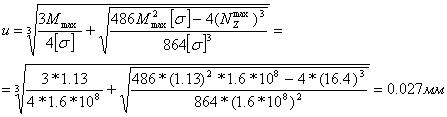
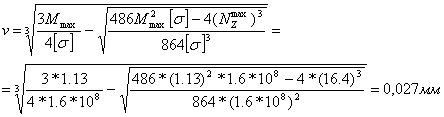
0 комментариев