Навигация
4.3. Рух по колу.
Одержимо умову руху тіла за коловою орбітою:
a = v2/r,
зумовлене гравітаційною силою:
mv2/r = GMm/r2
або
v = (MG/r)1/2.
Це є умова колової орбіти.
T = 2r/v
залежність періоду від радіуса знайдемо.
(2r)2/T2 = MG/r,
T2 = (2)2r3/MG – частинний випадок з закону Кеплера.
4.4. Еліптичні орбіти.
Опишемо властивості еліптичних орбіт:
F1 і F2 – фокуси еліпса. Для будь-якої точки Р.
F1Р + F2Р = const = 2a, остання рівність слідує з P(a, 0),
a – велика піввісь, b – мала піввісь.
В астрономії використовують a і e – ексцентриситет.
Відношення:
e = 
/2a,
пов’яжемо з b.
Нехай Р(0, b):
(ea)2 + b2 = a2,
e = (1 – b2/a2)1/2, причому 0<e<1
В частинному випадку
b = a еліпс стає колом і 
. Для орбіти Землі е =0.016.
4.5. Астрономічні одиниці
Зручно вибрати таку систему одиниць щоб 
. Для опису руху Землі, у якості просторової одиниці, вибирають велику піввісь земної орбіти. Вона називається астрономічна одиниця (а.о.), яка рівна 1а.о.=1.496 1011м.
У якості одиниць часу приймають 1рік = 3.15 1017с. У цих одиницях
Т=1рік, а=1а.о.
можемо записати
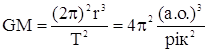
4.6. Зауваження до програмування
Будемо користуватись масивом чисел
/ Коментар, Основна програма
DECLARE SUB ff(y) – об’явити підпрограму
REM Коментар
REM PROGRAM
CALL ff(x) – викликати підпрограму
END
SUB name [( parameterlist)]
END SUB
FOR I=1 to n,
NEXT
де I – змінна циклу.
PRINT y,z видає на екран y, z
INPUT x, y - ввід даних
Точність чисельного розв’язку визначають, зменшуючи величину кроку 
до того часу, поки чисельний розв’язок не перестане залежати від кроку при заданому рівні точності, але це має виконуватись обережно, бо зростає число кроків і похибка округлення.
Найпростіша графіка.
CLS – очистити екран;
SCREEN 12 – графічна сторінка;
LINE (x1,y1) – (x2,y2), color, B – не замальовує рамку, якщо BF – замальовує.
CIRCLE (x1,y1), radius, PSET (x,y) – засвітити точку, PRESET (x,y) – погасити точку.
DO [white: until] condition
LOOP
DO
LOOP [{white: until}]
Оператор друкування по місцю:
LOCATE 5,5
VIEW PRINT 10 TO 15
Зупинка циклу з клавіатури при натисканні на клавішу “h”
DO UNTIL INKEY$ = ”h”
Задати логічні координати екрану
SCREEN 12
WINDOW (x1,y1)-(x2,y2)
Друкувати дані по формату експоненційної форми
PRINT USING “##.###^^^^”;x
4.7. Простий гармонічний осцилятор.
m d2x/dt2 =-kx;
F = - kx – повертаюча сила, нехай w02=k/m. Розв’язок цього рівняння можемо представити у наступному вигляді
x(t)=Acos(w0t + ).
A, - амплітуда і фаза визначаються з початкових умов.
Перевіркою правильності роботи програми може бути умова збереження повної енергії.
E = mv2/2 +kx2/2.
Рівняння руху, що описує затухаючі коливання
d2x/dt2 =-02x – g dx/dt + F(t)/m;
де другий доданок гальмуюча сила, третій – вимушуюча сила
F(t)/m = A0cos(wt).
Математичний маятник довжиною L.
Швидкість точки, що рухається по колу v = L dq/dt, тангенціальне прискорення a = L d2q/dt2.
Рівняння руху матиме вигляд
d2x/dt2 = - mg sinq.
Повна енергія представиться формулою
E = mL2 (dq/dt)2 /2 + mgL(1 – cosq).
8. Хвильові явища
Моделюємо лінійний ланцюг зв’язаних осциляторів. Виділимо властивості ланцюга, що відносяться до хвильових явищ. У наближенні неперервного ланцюжка виводиться лінійне хвильове рівняння. Демонструються інтерференція, дифракція, рефракція і поляризація. Розглядаємо ряд Фур’є і принцип Ферма.
8.1. Вступ
Для опису коливального і хвильового руху використовують такі поняття як період, амплітуда і частота. Як пов’язані ці величини. Розглянемо натягнутий шнур.
Імпульс розповсюджується по ньому зі швидкістю, що визначається натягом і інерційними властивостями шнура. Рух ділянки локалізований і здійснюється перпендикулярно руху хвилі.
На макроскопічному рівні спостерігаємо поперечну, хвилю на мікроскопічному рівні дискретні частинки здійснюють коливний рух.
Почнемо з мікроскопічної картини і розглянемо коливний рух лінійного ланцюга частинок сполучених пружинками. Рух моделюється, чисельно розв’язуючи рівняння руху для окремої частинки.
Побачимо, що енергія передається вздовж ланцюга, хоча кожний осцилятор знаходиться поблизу свого положення рівноваги.
Побачимо, що найзагальніший рух системи N часток можна представити як суперпозицію N незалежних простих гармонічних рухів.
Похожие работы
... ’язування задач у будь-якій галузі людської діяльності. Розв’язування задач у будь-якій галузі діяльності-це завжди одержання певних результатів обробки вхідних даних Для розв'язування задач комп'ютер озброєний найрізноманітнішими програмами, які поділяються на такі категорії: · операційні системи; · системи програмування; · прикладне програмне забезпечення. Оскі ...
... зичної освіти, а й важливий чинник загального розвитку школяра та професійного становлення у будь-якій галузі. Перша проблема, яку потрібно вирішити, упроваджую чи елементи комп'ютерного моделювання при вивченні фізики – вибір інструментальних засобів його реалізації. У час зародження сучасних інформаційних технологій єдиним способом було використання мов програмування високого рівня. За останні ...
... принтера також містить різні мови опису даних (Adobe PostScript, PCL і тощо.). Ці мови знову ж таки призначені для того, щоб забрати частину роботи у комп'ютера і передати її принтеру. Розглянемо фізичний принцип дії окремих компонентів лазерного принтера. 2.5.29 Фотобарабан Як вже писалося вище, найважливішим конструктивним елементом лазерного принтера є фотобарабан, що обертається, за ...
... , у принципі, здатний обробляти інформацію в 2L/L раз швидше в порівнянні зі своїм класичним аналогом. Звідси відразу видно, що маленькі квантові регістри (L<20) можуть служити лише для демонстрації окремих вузлів і принципів роботи квантового комп’ютера, але не принесуть великої практичної користі, тому що не зуміють обігнати сучасні ЕОМ, а коштувати будуть набагато дорожче. 1.3.Принципи ...
0 комментариев