Навигация
8.2. Зв’язані осцилятори.
Розглянемо простішу ніж у попередніх розділах модель.
Нехай ui-зміщення ії маси вздовж осі системи.
Кінці лівої і правої частинок нерухомі. Нерухомість виразимо U0 = UN+1=0.
Рівняння руху і-ї частинки
, i=2, …, N-1
, 
Це рівняння не тільки для повздовжніх коливань, але і для поперечних рівняння аналогічні.
Частоти нормальних коливань для kс=k
2n=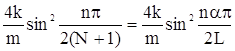
,
де N-число частинок, n-номер коливань n=1, …, N.
8.3. Фур’є аналіз.
Зміщення частинок можна представити у вигляді лінійної комбінації нормальних коливань, тобто лінійної суперпозиції синусоїдальних доданків.
Взагалі довільна періодична f(t) з періодом Т може бути записана у вигляді ряду Фур’є по sin i cos
f(t)=1/2 a0+
,
0-основна кругова частота, 0=2/Т
Доданки для n = 2, 3… являють другу і третю гармоніки. Коефіцієнти Фур’є виражаються
an =2/T
,bn =2/T
, 
На практиці використовують скінчене число членів n.
8.4. Хвильовий рух.
Ми виявили, що коливання окремих зв’язаних осциляторів призводить до розповсюдження енергії на довільну відстань. Знову запишемо рівняння для зміщення
, i=1, …, N.
Розглянемо перехід N прямує до нескінченості, a прямує до 0 за сталої довжини ланцюга. Це дискретне рівняння можна замінити хвильовим. ui(t) замінити на u(x, t), де x – неперервна змінна
похідну по часу записати як частинну похідну.
Через те що частинки розподілені неперервно, можна ввести величини M=m/a T=ka
легко показати що
Хвильове рівняння має величезну кількість розв’язків наприклад
Оскільки хвильове рівняння лінійне, то розв’язок можна представити у вигляді ряду Фур’є.
Якщо хвиля при русі зберігає свою форму то кажуть, що вона не диспергує, це зумовлено лінійністю зв’язку i k, інакше кожна гармоніка хвилі рухається з тією ж швидкістю. Якщо ж швидкість хвилі залежить від довжини хвилі (або хвильового числа), то кажуть, що диспергує, і цьому випадку форма хвилі змінюється з часом.
8.5. Інтерференція і дифракція.
Про інтерференцію говорять, коли змішуються хвилі від невеликого числа джерел, а про дифракцію коли від великого.
Дослід Юнга.
Дві щілини, монохроматичне світло. Щілини як точкові джерела
.
Електричне поле буде рівне сумі
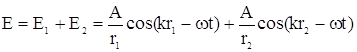
Інтенсивність дорівнює 
.
8.6. Поляризація.
Розглянемо явище, коли цікавить напрямок коливань. Для поперечної електромагнітної хвилі. Напруженість двовимірна векторна функція 
вздовж z-розповсюджується хвиля.
Ex (z,t) і Ey(z,t) Для монохроматичної хвилі =const, але компоненти коливаються незалежно.
Щоб сумарне поле знайти треба векторно скласти компоненти.
Похожие работы
... ’язування задач у будь-якій галузі людської діяльності. Розв’язування задач у будь-якій галузі діяльності-це завжди одержання певних результатів обробки вхідних даних Для розв'язування задач комп'ютер озброєний найрізноманітнішими програмами, які поділяються на такі категорії: · операційні системи; · системи програмування; · прикладне програмне забезпечення. Оскі ...
... зичної освіти, а й важливий чинник загального розвитку школяра та професійного становлення у будь-якій галузі. Перша проблема, яку потрібно вирішити, упроваджую чи елементи комп'ютерного моделювання при вивченні фізики – вибір інструментальних засобів його реалізації. У час зародження сучасних інформаційних технологій єдиним способом було використання мов програмування високого рівня. За останні ...
... принтера також містить різні мови опису даних (Adobe PostScript, PCL і тощо.). Ці мови знову ж таки призначені для того, щоб забрати частину роботи у комп'ютера і передати її принтеру. Розглянемо фізичний принцип дії окремих компонентів лазерного принтера. 2.5.29 Фотобарабан Як вже писалося вище, найважливішим конструктивним елементом лазерного принтера є фотобарабан, що обертається, за ...
... , у принципі, здатний обробляти інформацію в 2L/L раз швидше в порівнянні зі своїм класичним аналогом. Звідси відразу видно, що маленькі квантові регістри (L<20) можуть служити лише для демонстрації окремих вузлів і принципів роботи квантового комп’ютера, але не принесуть великої практичної користі, тому що не зуміють обігнати сучасні ЕОМ, а коштувати будуть набагато дорожче. 1.3.Принципи ...
0 комментариев