Навигация
Алгоритмы раскраски вершин графа
2. Алгоритмы раскраски вершин графа
Раскраской вершин графа G называется разбиение множества вершин Х на l непересекающихся подмножеств Х1, Х2, ..., Хl; ХÈХI; XiÇXj=Æ; i,jÎI={1,2,..,l}, (1)
таких, что внутри каждого подмножества Xi не должно содержаться смежных вершин (Xi-внутренне устойчивые подмножества).
Если каждому подмножеству хi поставить в соответствие определенный цвет, то вершины внутри этого подмножества можно окрасить в один цвет, вершины другого подмножества Хj - в другой цвет и т.д. до раскраски всех подмножеств.
В этом случае граф называется 1-раскрашиваемым. Наименьшее число подмножеств, на которое разбивается граф при раскраске, называется хроматическим числом c(G).
Очевидно, что полный граф Kn можно раскрасить только n цветами, следовательно, c(Кn) =n. Для связного графа G= (Х,U) с числом ребер m, где (n-1)<m<n(n-1)/2 верхняя оценка хроматического числа c(G) определяется как
c(G)![]()
Нижней оценкой c(G) является число вершин в наибольшем полном подграфе графа G,т.е. его плотность. Известно утверждение, что для любого графа c(G)<1+max r(xi),где хi Î Х, iÎI={1,2,...,n},r(xi)- локальная степень вершины хi.Приводятся также следующие оценки:
c(G)³n2/(n2-m2); c(G)£n+1-c(Gд),
где Gд= К\G ( дополнение графа G до полного К).
Задача раскраски вершин (поиска хроматического числа) графа может быть решена точными или приближенными алгоритмами.
К точным алгоритмам относятся: алгоритм, использующий метод Магу – Вейсмана; алгоритмы, основанные на рассмотрении максимальных r - подграфов и алгоритмы на основе методов целочисленного линейного программирования.
К приближенный алгоритмам раскраски относятся алгоритмы, основанные на упорядочивании множества вершин графов , последовательном удалении из графа вершин, имеющих максимальную степень и на анализе подмножеств смежности вершин.
2.1 Точные алгоритмы
Алгоритм, использующий метод Магу - Вейссмана
1. Для графа G (Х,U) построим семейство МВУП F={Fj}, где j= 1,... ,1; 1 - число МВУП.
1. 2. Составим матрицу
Cij=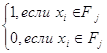
3. Для. каждой вершины графа G =(Х,U) по матрице С находим суммы тех FjÎF, в которые она входит, и записываем произведение этих сумм.
4. Раскрываем скобки по правилам булевой алгебры и выбираем слагаемое, состоящее из наименьшего числа сомножителей.
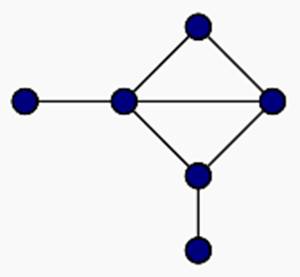
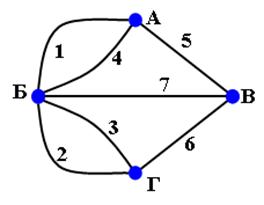
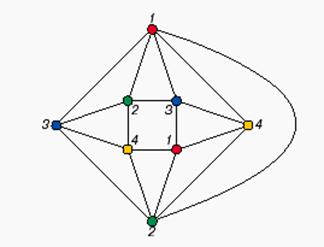
Рассмотрим работу описанного алгоритма на примере графа (рис.16).Согласно алгоритму Магу - Вейссмана для поиска семейства МВУП составим произведение
ПG = (X1 +Х2) (Х1+ХЗ) (Х2+ХЗ) (Х2+Х5) (Х2+Х7) (ХЗ+Х5) (ХЗ+Х6) (ХЗ+X7)*
(Х4+Х5) (Х4+Х6) (Х4+Х7) = (Х1+Х2ХЗ)*(Х2+ХЗХ5Х7) (ХЗ+Х5Х6Х7) (Х4++Х5Х6Х7) = (Х1Х2+Х1ХЗХ5Х7+Х2ХЗ+Х2ХЗХ5Х7) (ХЗХ4+ХЗХ5Х6Х7+Х4Х5Х6X7++Х5ХбХ7) =Х1Х2Х3Х4+Х1Х2Х5ХбХ7+Х1Х3Х4Х5X7+Х1Х3Х5Х6Х7+Х2ХЗХ4+
+Х2ХЗХ5Х6Х7. Рi= Х1Х2ХЗХ4 поглощается подмножеством Р5 =Х2ХЗХ4.
Используя условие, что в ПG в качестве сомножителей будут вершины Х\Рj получаем следующее семейство
МВУП F={F1,F2,F3,F4,F5}: F1=X\{X1,X2,X5,X6,X7}={X3,X4}; F2={X2,X6}; F3={X2,X4}; F4={X1,X5,X6,X7}; F5={X1,X4}.
Составляем матрица C
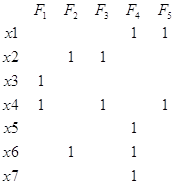
Для каждой вершины Хi Î Х по матрице С составим суммы тех FjÎF, в которые оно входит и запишем произведение этих сумм
ПС=(F4+F5)(F2+F3)F1*(F1+F3+F5)F4*(F2+F4)F4=(F2+F3F4)F1F4=F1F2F4+F1F3F4.
Каждое из двух полученных слагаемых содержит в неявном виде все вершины графа G =(Х,U), Таким
образом, для раскраски требуется минимум 3 цвета. Раскроем слагаемые и удалим дублирующие вершины.
В результате получаем два варианта решения:
F1F2F4={ХЗ,Х4;Х2;Х1,Х5,Х6,Х7} или
F1F2F4={ ХЗ,Х4;Х2X6;Х1,Х5,Х7};
F1F3F4={X3;X2,Х4;Х1,Х5,Х6,Х7}
или F1F3F4={XЗ,X4;X2;X1,X5,Xб,X7}.
Первый и последний варианты совпали. Получены три различных варианта минимальной раскраски вершин графа.
Похожие работы
... набором типовых подсхем - Автоморфизм графов конструктивное перечисление структурных изомеров для производных органических соединений синтез тестов цифровых устройств 2.2. Нахождение кратчайших путей в графе Начальные понятия Будем рассматривать ориентированные графы G = <V, E>, дугам которых приписаны веса. Это означает, что каждой дуге <u, ...
... практичных алгоритмов оптимизированного перебора, позволяющих за разумное время осуществлять распараллеливание достаточно больших участков. Анализ работ, посвященных оптимизации кода для процессоров с параллелизмом на уровне команд показывает, что для достижения наилучших результатов необходимо применение комплекса оптимизаций, среди которых можно выделить следующие классы. Преобразования циклов ...
... канальных трассировщиков. Иными словами - ГБД не должна содержать циклических конфликтов. 3. Разработка информационного содержания базы знаний для решения вертикальных конфликтов БЗ для решения вертикальных конфликтов (ВК) в процессе трассировки строится на основе продукционных правил. Ввиду того, что возможны различные варианты вертикальных конфликтов, целесообразным представляется проведение ...
... Рассела и во многом базируется на работе Бертрана Рассела и Альфреда Уайтхэда «Principia Mathematica» (этот фундаметальный трёхтомник математической логики до сих пор не издан на русском языке)[8]. Заключение Прародителем информатики является кибернетика, основанная американским математиком Норбертом Винером, опубликовавшим в 1948 году одноименную книгу. Основоположником ...
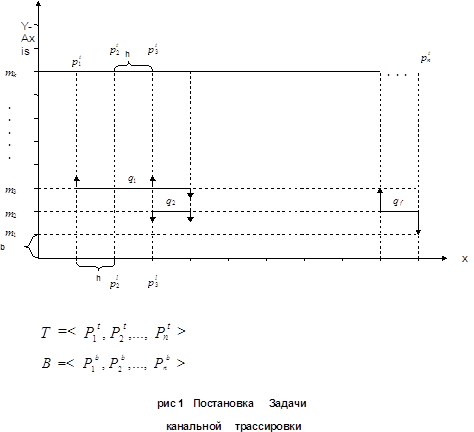

0 комментариев