Навигация
ПРОГРАММА И ПРИМЕР РЕАЛИЗАЦИИ АЛГОРИТМА БПФ С ПРОРЕЖИВАНИЕМ ПО ВРЕМЕНИ
36424
знака
11
таблиц
11
изображений
3. ПРОГРАММА И ПРИМЕР РЕАЛИЗАЦИИ АЛГОРИТМА БПФ С ПРОРЕЖИВАНИЕМ ПО ВРЕМЕНИ
Ниже при водится программа вычисления БПФ с прореживанием по времени по способу с замещением и рассматриваются при меры реализации этой программы.
Программа 1 - быстрое преобразование Фурье с основанием два и прореживанием по времени. Программа осуществляет алгоритм БПФ с основанием два и прореживанием по времени комплексной или вещественной последовательности х(п) длиной N отсчетов. Вещественные составляющие отсчетов исходной последовательности записываются в массив А1(N), а мнимые - массив А2(N). В программе для ознакомления с ее работой предусмотрено формирование входной последовательности, соответствующей отсчетам полигармонического сигнала
 |
(3.1)
строки (80-240). При использовании программы для выполнения БПФ произвольной последовательности необходимо заменить строки 80-240, организовав ввод исходной последовательности.
Основными этапами обработки являются: ввод исходных данных (строки 50-240), двоично-инверсная перестановка исходной последовательности (строки 250-350), собственно алгоритм БПФ (строки 360-510), расчет амплитуд и фаз анализируемого сигнала по результатам БПФ (строки 520-590) и вывод результатов (строки 600-690). Пользователю выводятся в виде таблицы значения номера компоненты (гармоники) БПФ, вещественная и мнимая ее составляющие [Аl (1) и А2 (1)], амплитуда и фаза соответствующей гармоники [R (1) и Fl (1)].
Пример 2. Реализация БПФ вещественного сигнала 
содержащего три составляющие при значениях параметров: А0=2, w0=
0=0, А1=I, w1=0,125, 
1=0,7854, А2=3, w2=0,3125, 2=1,57.
В качестве исходных данных последовательно вводятся значения:
N=16; J=3; А(0)=2; w(0)=0; w1(0)=0; A(1)= 1; w(1)=0,125; w1 (1)=0,7854; А (2)=З; w(2)=0,3125; w1(2)= 1,57; I 9= 1;
Пример 3. Реализация БПФ комплексного сигнала (3.1), содержащего три составляющие (J=3), при значениях параметров Ak, wk и k таких же, как
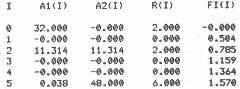
в примере 2. Ввод исходных данных аналогичен примеру 2, за исключением того, что значение I 9=0.
4. АЛГОРИТМ БПФ С ПРОРЕЖИВАНИЕМ ПО ЧАСТОТЕ
Рассматриваемый ниже алгоритм вычисления ДПФ (1.1) отличается тем, что входная последовательность х(пТ), п=0,..., N -1, разбивается на две последовательности посередине (т. е. одна последовательность для n=0...N/2-1, а другая - для п=N/2...N-1) и эта процедура продолжается для каждой новой последовательности до тех пор, пока не получается искомая выходная одноэлементная последовательность Х (k); при этом величины Х (k) уже оказываются в выходном массиве в «прореженном» порядке и их приведение к естественному порядку связано с инверсией двоичного представления индексов k в вычисленных значениях Х (k).
Итак, запишем ДПФ (1.1) в виде:
(4.1)
Учитывая, что 
=
получаем
. (4.2)
Подставив вместо k в (4.2) значение 2k или (2k+ 1), получим выражения для четных и нечетных отсчетов ДПФ: .
; (4.3)
, (4.4)
где теперь для значений
:
Х0 (п)=х(п) +x(n+N/2); (4.5)
Х1(п)=х(п) -х(n+N/2). (4.6)
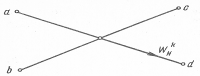
Рисунок 5 - Выполнение базовой операции «бабочка»
Следовательно, вычисление N-точечного ДПФ X(k) сводится к вычислению двух N/2-точечных ДПФ при четных и нечетных значениях k для функций х0(п) и x1 (п) и выполнению базовой операции «бабочка» (рис.5) отличие операции «бабочка» здесь заключается в том, что комплексное умножение выполняется после операции сложения-вычитания.
Ту же процедуру можно теперь применить к x0 (п) и х1 (п) и перейти от N/2-точечных ДПФ к N/4-точечным ДПФ и, таким образом, свести вычисление Х (2k) и Х (2k + 1) через Х (4k), X(4k+2), X(4k+ 1), X(4k+3). Продолжив этот процесс, перейдем в конечном итоге к 2-точечным ДП Ф с последующим прямым вычислением всех выходных отсчетов Х (k). Полный алгоритм БПФ с прореживанием по частоте и его программная реализация аналогичны рассмотренным выше для метода БПФ с прореживанием по времени.
Необходимо отметить, что в обоих алгоритмах БПФ - и с прореживанием по времени, и с прореживанием по частоте требуется примерно Nlog2 N операций (комплексных умножений) и оба алгоритма могут быть реализованы по способу с замещением, используя только один массив ячеек памяти. В обоих алгоритмах должна быть предусмотрена процедура двоичной инверсии - на входе (при прореживании по времени) или на выходе (при прореживании по частоте).
Похожие работы
... учесть введением в блок-схему дополнительного .источника шума [11]. Расстояние между отсчетами должно удовлетворять теореме Найквиста для двумерных колебаний [1]. Устройства для дискретизации и квантования изображений основаны на технике микроденситометрии. В подобных системах на пленку проектируется луч света с интенсивностью I1. Интенсивность I2 света, прошедшего сквозь пленку (или отраженного ...
... Интересным примером применения спецпроцессора СПФ СМ явилась обработка радиолокационных сигналов зондирования поверхности планеты Венера, которое проводилось со спутника. Глава 3. Применение цифровой обработки сигналов. 3.1 Шумоподавление для звука Звуковой сигнал, записываемый в реальных акустических условиях, часто содержит нежелательные шумы, которые могут порождаться окружающей средой ...
... , расположенной напротив одного из ушей, к точке, расположенной перед человеком. Дилэй применяется, прежде всего, в том случае, когда запись голоса или акустического музыкального инструмента, выполненную с помощью единственного микрофона, встраивают в стереофоническую композицию. Этот эффект служит основой технологии создания стереозаписей. Подробные рекомендации по применению задержки в этих ...
... построения оптических систем и сетей связи В результате изучения данной дисциплины студент должен: знать: принципы построения инфокоммуникационных сетей (ПК-1); основные характеристики первичных сигналов связи (ПК-3); принципы построения проводных и радиосистем передачи с частотным и временным разделением каналов (ПК-1); основные характеристики каналов и трактов (ПК-3); принципы построения ...
0 комментариев