Навигация
ПРИМЕНЕНИЕ МЕТОДА БПФ ДЛЯ ВЫЧИСЛЕНИЯ ОБРАТНОГО ДПФ (ОДПФ)
36424
знака
11
таблиц
11
изображений
5. ПРИМЕНЕНИЕ МЕТОДА БПФ ДЛЯ ВЫЧИСЛЕНИЯ ОБРАТНОГО ДПФ (ОДПФ)
По определению (1.2) ОДПФ х(пТ) N-точечной последовательности X(k), k=0, 1,..., N-1, выражается соотношением
(5.1)
причем в общем случае и х(пТ), и Х(k)-комплексные. Пусть х(пТ) и Х*(k)-последовательности, комплексно сопряженные соответственно с х(пТ) и X(k). Согласно (5.1) можно записать
(5.2)
Но выражение суммы в правой части (5.2) есть прямое ДПФ последовательности Х*(k), k=0,..., N-1, и, следовательно, эта сумма может быть вычислена при помощи рассмотренных алгоритмов и программ БПФ.
Таким образом обеспечивается вычисление последовательности Nx* (пТ) и для определения х(пТ) остается взять комплексно сопряженное с Nx*(пТ) выражение и разделить его на N:
 |
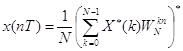(5.3)
6. ПРИМЕНЕНИЕ БПФ ДЛЯ ВЫЧИСЛЕНИЯ РЕАКЦИИ ЦФ
Вычисление реакции у(пТ) ЦФ с импульсной характеристикой h(пТ), п=0, 1,..., N-1, на входное воздействие х(пТ), п=О, 1,...M -1, может быть выполнено на основе алгоритма свертки
(6.1)
при п=0, 1,..., N+M-2.
Применение алгоритмов БПФ позволяет выполнить эффективное вычисление выходной последовательности у(пТ) ЦФ. С этой целью следует определить ДПФ H(k) и X(k) в N+M-1 точках для последовательностей h(пТ) и х(пТ), затем определить ДПФ Y(k)=H(k)X(k) выходной последовательности у(пТ). Вычисление у (пТ) по ОДПФ Y(k) выполняется, например, по алгоритму (5.3). Для вычисления ДПФ и ОДПФ используются алгоритмы БПФ. Отметим, что если длина М последовательности х(пТ) велика, то реализация упомянутого выше алгоритма вычисления у(пТ) связана со значительной временной задержкой (для накопления всех М выборок х(пТ)). С целью уменьшения этой задержки можно входную последовательность х(пТ) разбить на отрезки xi(пТ) каждый длиной L и обрабатывать каждый из них независимо от других. Представим
(6.2)
Тогда можно (6.1) записать в виде
 |
(6.3)
Где частная свертка
 |
(6.4)
Таким образом можно начинать расчет методами БПФ частных сверток и формировать у(пТ) путем соответствующего суммирования элементов частных сверток [2].
7. ДРУГИЕ БЫСТРЫЕ АЛГОРИТМЫ ВЫЧИСЛЕНИЯ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
7.1 Обобщенный алгоритм Кули-Тьюки с произвольным основанием с множителями поворота
Кроме рассмотренных выше классических алгоритмов БПФ известных как алгоритмы Кули-Тьюки по основанию 2, известно множество других. Некоторые из них позволяют существенно повысить эффективность вычисления дискретного преобразовании Фурье. Так, алгоритмы Винограда при равном числе сложении требуют примерно в 5 раз меньше умножений, чем алгоритмы Кули-Тьюки.
В основе всех известных алгоритмов лежит принцип разбиении исходного ДПФ на совокупность мало точечных. Различие заключается в способах вычисления мало точечных алгоритмов и последующего объединения частичных результатов. При этом размер преобразования не обязательно равен степени двух, т. е. становится возможным БПФ произвольной длины, что очень важно для ряда практических задач. Так, в технике связи при цифровом преобразовании многоканальных сигналов размер БПФ определяется числом объединяемых каналов.
Кратко рассмотрим только некоторые, наиболее важные алгоритмы, на основе которых впоследствии возникло множество различных эффективных модификаций. Это: 1) обобщенный алгоритм Кули-Тьюки с произвольным основанием с множителями поворота; 2) алгоритм простых множителей Гуда-Винограда; 3) алгоритм Винограда.
Для простоты изложения везде будем полагать N=N1N2, где N - длина преобразования. Очевидно, приводимые ниже положения легко могут быть перенесены на более общий случай, когда 
Обобщенный алгоритм Кули-Тьюки с произвольным основанием с множителями поворота. Итак, пусть N=N1N2, гдеN1 и N2 - положительные целые. Покажем, что в этом случае вычисление исходного N-точечного ДПФ можно свести к вычислению N1 N2-точечных и N2 N1-точечных ДПФ и N умножениям на множители поворота 
. Для этого в выражения для ДПФ (1.1)
 |
(7.1)
где 
, необходимо сделать подстановку:
k=k1 +k2N2, k1=0, …., N2-1; k2=0, …., N1-1; (7.2)
n=n1 +n2N2, n1=0, …., N2-1; n2=0, …., N2-1. (7.3)
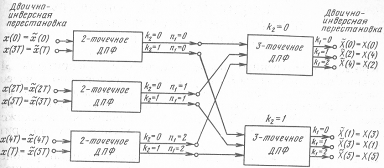
Рисунок 6 - Сигнальный граф алгоритма
Тогда ДПФ (7.1) преобразуется к виду
 |
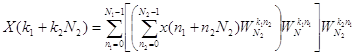(7.4)
Таким образом, полученный алгоритм включает в себя две основные ступени: на первой ступени переставленные в соответствии с (7.3) входные выборки подвергаются N2-точечному преобразованию Фурье. На второй ступени производится вычисление N1-точечных ДПФ. Между первой и второй ступенями осуществляется операция поворота путем умножения на поворачивающие множители 
. Полученная последовательность на выходе ДПФ должна быть переставлена в соответствии с (7.2).
Пример 4. Пусть N=6, N1=3, N2=2. Положим k=k1+k2*2; n=n1+ +n2*3; n1k2=0,1,2; n2k1=0, 1.
Тогда
 |
Соответствующий сигнальный граф алгоритма изображен на рис.6.
Рассмотренный подход может быть положен в основу синтеза алгоритмов БПФ Кули-Тьюки с произвольным постоянным основанием. Наибольшую популярность получили алгоритмы с основаниями 4 и 8, позволяющие повысить эффективность вычисления ДПФ по сравнению с классическими алгоритмами по основанию 2. Отметим, что алгоритмы с основанием 2 также могут быть получены с использованием рассмотренного подхода. Таким образом, рассмотренный метод синтеза является общим и позволяет синтезировать различные модификации алгоритма Кули - Тьюки с произвольными постоянным и смешанным основаниями.
Похожие работы
... учесть введением в блок-схему дополнительного .источника шума [11]. Расстояние между отсчетами должно удовлетворять теореме Найквиста для двумерных колебаний [1]. Устройства для дискретизации и квантования изображений основаны на технике микроденситометрии. В подобных системах на пленку проектируется луч света с интенсивностью I1. Интенсивность I2 света, прошедшего сквозь пленку (или отраженного ...
... Интересным примером применения спецпроцессора СПФ СМ явилась обработка радиолокационных сигналов зондирования поверхности планеты Венера, которое проводилось со спутника. Глава 3. Применение цифровой обработки сигналов. 3.1 Шумоподавление для звука Звуковой сигнал, записываемый в реальных акустических условиях, часто содержит нежелательные шумы, которые могут порождаться окружающей средой ...
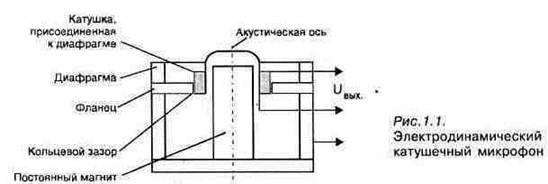
... , расположенной напротив одного из ушей, к точке, расположенной перед человеком. Дилэй применяется, прежде всего, в том случае, когда запись голоса или акустического музыкального инструмента, выполненную с помощью единственного микрофона, встраивают в стереофоническую композицию. Этот эффект служит основой технологии создания стереозаписей. Подробные рекомендации по применению задержки в этих ...
... построения оптических систем и сетей связи В результате изучения данной дисциплины студент должен: знать: принципы построения инфокоммуникационных сетей (ПК-1); основные характеристики первичных сигналов связи (ПК-3); принципы построения проводных и радиосистем передачи с частотным и временным разделением каналов (ПК-1); основные характеристики каналов и трактов (ПК-3); принципы построения ...
0 комментариев