Навигация
Геометрия места точек на плоскости
Гатчинский социально-гуманитарный институт (филиал)
автономного образовательного учреждения высшего профессионального образования
Ленинградский государственный университет им. А. С. Пушкина
Факультет: МФИ
КУРСОВАЯ РАБОТА
Дисциплина: Геометрия
Геометрия места точек на плоскости
Студент: Кузвесов И. Н.
3-го курса
Научный руководитель:
Игнатьева И. В.
Гатчина
2009
План
Введение
1. Определение геометрического места точек
2. Сущность метода геометрических мест
3. Основные геометрические места точек на плоскости
4. Примеры задач на геометрические места точек
Список литературы
Введение
Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Такое название этой науке было дано потому, что в древнее время главной целью геометрии было измерение расстояний и площадей на земной поверхности.
Легко представить себе поверхность как границу тела: плоская поверхность стола, сферическая поверхность мяча, цилиндрическая поверхность трубы. Но такое представление не полно. Возьмем тонкую замкнутую проволоку изогнутой формы и опустим её в мыльную пену. Если мы осторожно извлечем её из пены, то увидим, что просвет в проволочном "кольце" затянут тончайшей мыльной пленкой. Правильно представлять себе поверхность именно как тонкую пленку (но лишенную всякой толщины).
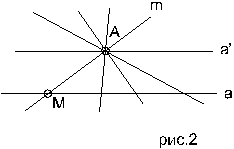
Важнейшая и простейшая поверхность - плоскость. Прямая m, лежащая в плоскости, разбивает её на две части - полуплоскости; точки этой прямой и только они являются общими точками обеих полуплоскостей. Если А - точка одной полуплоскости, а В - другой, то отрезок АВ пересекает границу m полуплоскостей в некоторой точке С, лежащей между А и В.
Плоскости задаются тремя точками и обозначаются часто так: плоскость АВС или PQR и т.д. Иногда бывает проще обозначать плоскость одной буквой греческого алфавита: a, b, g, d...
Под фигурой обычно понимают некоторое сочетание определенным образом расположенных в одной плоскости (а иногда и в пространстве) элементов: точек, прямых, лучей, отрезков (иногда и плоскостей).
Под телом понимают обычно часть пространства, ограниченную какой-либо замкнутой поверхностью. Так, конус - тело, ограниченное канонической поверхностью с боков и плоским круглым основанием снизу. Куб - тело, ограниченное шестью квадратными гранями, и т.д. Курс геометрии традиционно подразделяется на планиметрию и стереометрию; в планиметрии рассматриваются свойства различных фигур (треугольников, многоугольников, окружностей), лежащих в плоскости. В стереометрии изучаются свойства пространственных фигур и тел.
1. Определение геометрического места точек
Геометрическое место точек – это множество всех точек, удовлетворяющих определённым заданным условиям.
Пример 1. Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO AB и AO = OB:
Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d. Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
Пример 2. Окружность - это геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра (одна из этих точек – А).
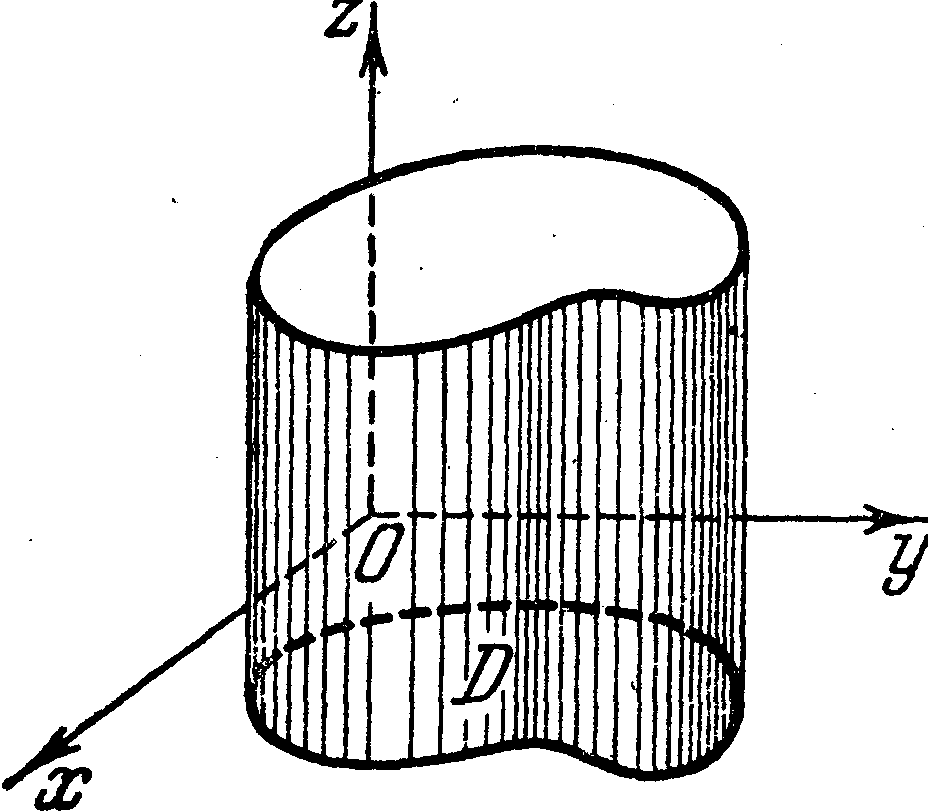
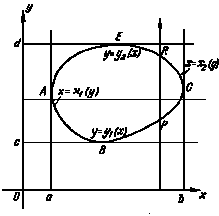
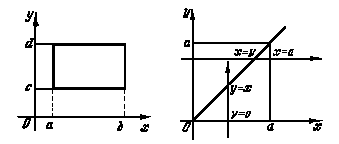
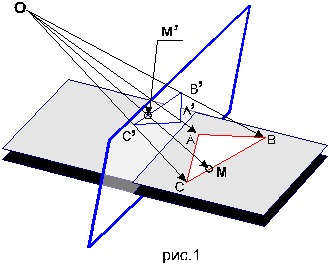
Тогда отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности AmB, называется дугой. Прямая PQ, проходящая через точки M и N окружности, называется секущей, а её отрезок MN, лежащий внутри окружности - хордой. Хорда, проходящая через центр круга например, BC называется диаметром и обозначается d или D. Диаметр – это наибольшая хорда, равная двум радиусам (d = 2r). Предположим, дана точка А (7; 3; 5); эта запись означает, что точка А определяется координатами х = 7, у = 3, z = 5. Если масштаб для построения чертежа задан или выбран, то откладывают на оси х от некоторой точки О отрезок ОАХ, равный 7 единицам, и на перпендикуляре к этой оси, проведенном из точки Ах, отрезки АХА' = 3 ед. и АХА" = 5 ед. Получаем проекции А' и А". Для построения достаточно взять только ось х. Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям. Например, отрезок ОАХ - выражает абсциссу точки А, отрезок АХА' - ее ординату, отрезок АХА" - аппликату. Если задается лишь абсцисса, то этому соответствует плоскость, параллельная плоскости, определяемой осями у и z. Действительно, такая плоскость является геометрическим местом точек, у которых абсциссы равны заданной величине. Если задаются две координаты, то этим определяется прямая, параллельная соответствующей координатной оси.
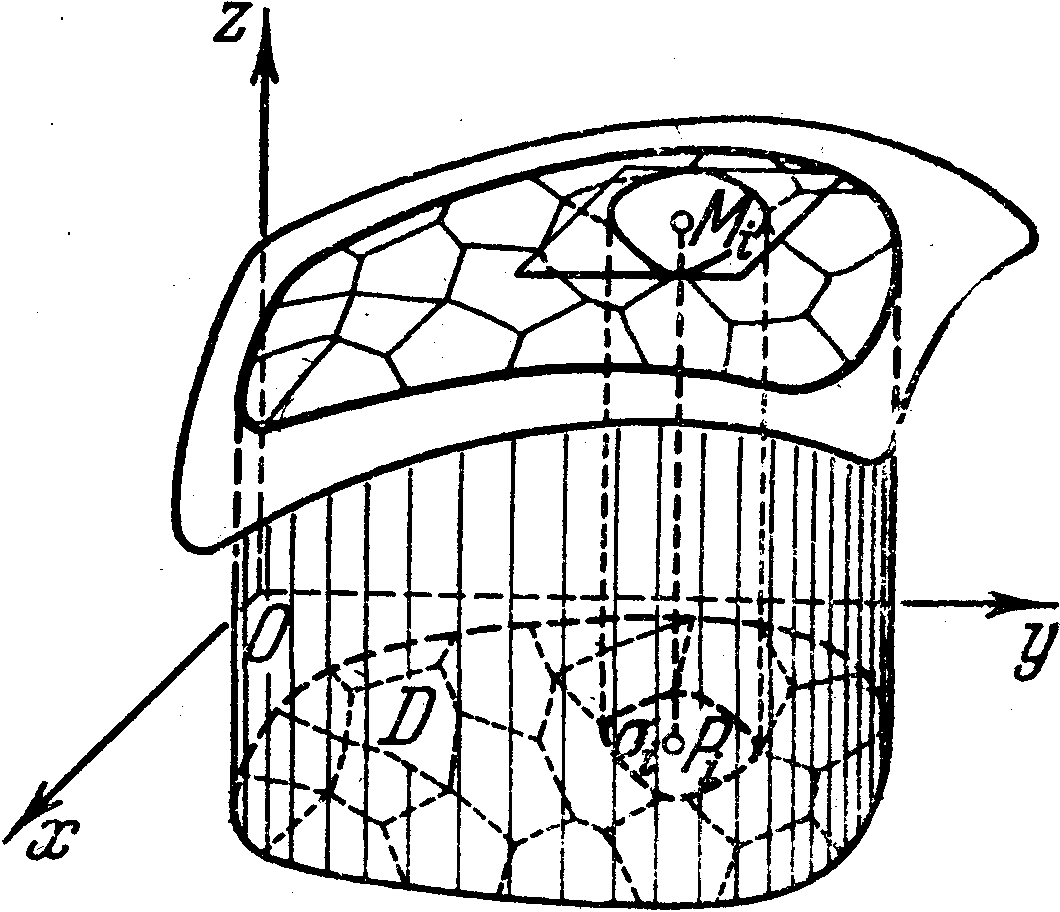
Например, имея заданными абсциссу и ординату, получаем прямую, параллельную оси z (это прямая АВ). Она является линией пересечения двух плоскостей _ и _, где _ - геометрическое место точек с равными ординатами. Прямая АВ служит геометрическим местом точек, у которых равны между собой абсциссы и равны между собой ординаты. Если задаются все три координаты, то этим определяется точка. Точка К, полученная в пересечении трех плоскостей, из которых _ есть геометрическое место точек по заданной абсциссе, _ - по заданной ординате и _ - по заданной аппликате. Точка может находиться в любом из восьми октантов. Следовательно, нужно знать не только расстояние данной точки от той или иной плоскости координат, но и направление, по которому надо это расстояние отложить; для этого координаты точек выражают относительными числами.
Похожие работы
... информационной причинности взаимодействий (нейтрализация энтропии), связанной с процессами отражения степеней упорядоченности (возбуждений), обладание универсальной системой пространственно-временных отношений, выделяют “абсолютный квант” в феноменальное явление физической природы. Он может быть неожиданным материальным воплощением той начальной активной субстанции, которую объективный идеализм, ...
... Q(у) такого сечения равна , где у при интегрировании считается величиной постоянной. Интегрируя затем Q(у) в пределах изменения у, т. е. от c до d, мы придем ко второму выражению для двойного интеграла (Б) Здесь интегрирование совершается сначала по х, а потом по у. .Формулы (А) и (Б) показывают, что вычисление двойного интеграла сводится к последовательному вычислению двух обыкновенных ...
... сопряжена с P, Q. Т. е. эти пары взаимно гармонические. Как и свойство взаимной раздельности пар, свойство гармонической сопряжённости инвариантно относительно проектирования (это инвариант проективной геометрии) (рис.14). Т. e. если P, Q и S, T гармонически сопряжённые пары, то после проектирования из некоторого центра O на прямую и получим тоже гармонически сопряжённые пары P/, Q/ и S/, T/. ...
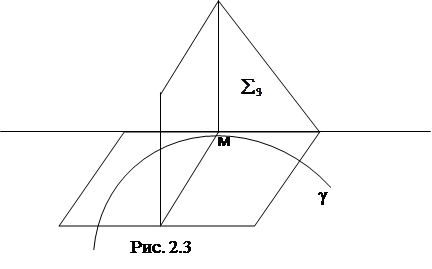
... Известно, что соприкасающаяся плоскость к кривой g в точке M определяется векторами . Таким образом, исходя из формулы (23) получим, что соприкасающаяся плоскость ребра возврата g - есть касательная плоскость к торсу. Рассмотрим торс пространства 1R4, порожденной кривой определяемый уравнением (23). Введем координатные линии на поверхности торса: u-линии (v=c) и v-линии (u=c). Найдем скалярное ...

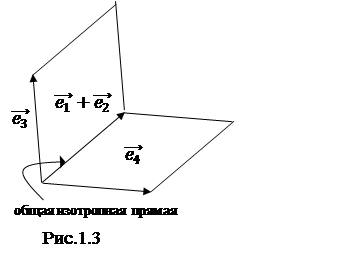
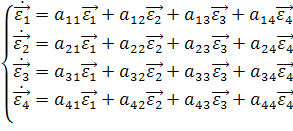
0 комментариев