Навигация
Найдите производную функций в данных точках
29946
знаков
3
таблицы
2
изображения
5. Найдите производную функций в данных точках.
I в.: f(x) = cos x, при х = 
II в.: f(x) = tg x, при х = 
III в.: f(x) =cos 2x, при х = 
IVв.: f(x) = x2 + 4x + 72, при х = -5
Приложение 3
Конспект урока на тему "Производная"
1. Задачи, приводящие к понятию производной.
Рассмотрим движение материальной точки М вдоль оси Ох (рис.1). За начало отсчета (точка О) примем положение материальной точки в момент времени t = 0. Пусть в момент времени t координата движущейся точки х равна f(t), т.е. координата х материальной точки есть функция времени:
Х = f(t), t Є [0; T]
О М х
Эта функция называется законом движения, задается формулой:
X = Vt
На практике поезда, автомобили движутся равномерно и прямолинейно лишь на некоторых участках, а в общем случае их движение неравномерное. При неравномерном прямолинейном движении материальная точка за разные, но равные по длительности промежутки времени может совершать разные как по времени, так и по направлению перемещения. Для неравномерного движения вводится понятие средней скорости Vср, которая зависит от выбора моментов времени t0 и t1:
Vср (t1, t0) = 
Проиллюстрируем сказанное примером. Из курса физики известно, что свободное падение тел в поле тяжести Земли является неравномерным движением и совершается по закону х = 
, где g – ускорение свободного падения. Его средняя скорость за первую секунду движения, т.е. за промежуток времени от момента t0 = 0 до момента времени t1 = 1, равна:
Vср(1, 0) = 
,
в то время как для второй секунды движения (t1 = 2, t0 = 1) она уже равна в три раза большему значению:
Vср(2, 1) =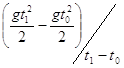 
= 
Средняя скорость не может полностью характеризовать неравномерное движение. Для полной характеристики вводят так называемую мгновенную скорость. Очевидно, что средняя скорость Vср (t1, t0) тем полнее характеризует движение за промежуток времени от t0 до t1, чем меньше длительность этого промежутка. Предел средней скорости за промежуток времени от t0 до t1 при t1, стремящимся к t0, называется мгновенной скоростью V(t0) в момент времени t0, т.е.:
|
|
|
|
|
|
|
|
|
|
Похожие работы
... = [х ln х] – х(dх/х) = = [х ln х] – [х] = 2 ln2 – 1 = ln4 – 1 3.Исторические сведения о возникновении и развитии основных понятий. В математике XVII в. самым большим достижением справедливо считается изобретение дифференциального и интегрального исчисления. Сформировалось оно в ряде сочинений Ньютона и Лейбница и их ближайших сотрудников и учеников. Введение в математику методов анализа ...
... некоторых математических теорем Выведем из физических соображений некоторые ограничения на функцию, которая может служить законом движения макроскопического тела, а затем сравним их с условиями основных теорем дифференциального исчисления. (А) Начнем с простого соображения о том, что реальный физический эксперимент имеет свое начало и конец, т.е. протекает за конечный отрезок времени. В силу ...
... . . . . x –2 1 – 0 – 0 + вогнутая перегиб выпуклая перегиб вогнутая Отсюда следует, что функция выпуклая при , вогнутая при . Точки , – точки перегиба. 2. Дифференциальное исчисление функций и его приложение» 1. Провести полное исследование свойств и построить эскиз графика функции . Решение. 1) Область определения функции ...
... Спорщики возьмут в руки перья и, сказав: “Начнем вычислять” - примутся за расчеты. Как уже отмечалось, Лейбниц одновременно с Ньютоном и независимо от него открыл основные принципы дифференциального и интегрального исчислений. Теория приобрела силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование - взаимно обратные операции. Об этом свойстве хороню знал и ...
0 комментариев