Навигация
Графическое представление динамического ряда
1.2 Графическое представление динамического ряда
В анализе динамических рядов наряду с табличной формой широко используются графические представления. Основным способом отображения динамических рядов является статистическая кривая. Для ее построения берется система прямоугольных координат. На оси абсцисс откладывается время, а на оси ординат - уровни динамического ряда. В итоге получены две статистические кривые экспорта и импорта, которые дают наглядное представление о динамике исследуемого ряда:
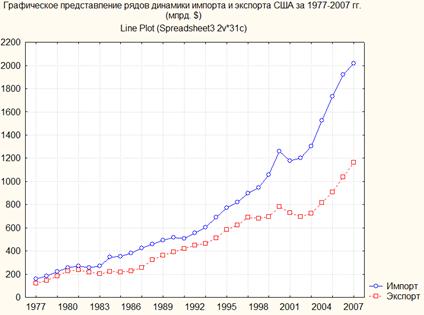
Рис. 1. Графическое представление динамики импорта и экспорта США (млрд. $)
Мы видим, что существует тенденция увеличения объема экспорта и импорта на протяжении рассматриваемого периода, но эта закономерность не проявляется четко на каждом конкретном уровне. Например, можно выделить резкое снижение объема экспорта и импорта 1999г. по 2002 г.
Построение и анализ рядов динамики позволяет выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно длительной динамике. На основную закономерность динамики накладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уровней, именуемой трендом, и дальнейшее прогнозирование на ее основе являются главными задачами анализа рядов динамики.
В курсовом проекте необходимо рассчитать показатели изменения уровней динамических рядов, средние показатели, затем определить тренд каждого ряда.
1.3 Расчет показателей изменения уровней динамических рядов и средних показателей
Анализ динамических рядов социально-экономических явлений обычно начинают с рассмотрения статистик, расчет которых не требует какой-либо предварительной обработки анализируемого динамического ряда. Речь идет о так называемых показателях динамического ряда, позволяющих пояснить характер, скорость, интенсивность и направление развития изучаемого явления за определенный промежуток времени.
В результате того или иного сопоставления уровней динамического ряда формируется система абсолютных и относительных показателей динамики, к числу которых относятся абсолютные приросты (и их среднее значение), ускорение, коэффициенты роста (и их среднее значение), коэффициенты прироста (и их среднее значение), абсолютное значение одного процента прироста.
Показатели абсолютного прироста и темпа роста, рассчитанные путем сопоставления каждого текущего уровня ряда (yt) с непосредственно ему предшествующим (yt-1), называются цепными, а рассчитанные путем сопоставления с уровнем, принимаемым за базу - базисными. В данном случае за базу принимается первый уровень ряда, т.е. значения экспорта и импорта Франции в 1977 г.
Абсолютным приростом называется разность последующего и предыдущего уровней ряда динамики:
![]() ,
,
где:
yt— уровень ряда динамики в момент времени t;
yt-1— уровень ряда динамики в момент времени t-1;
Dt— абсолютный прирост.
За весь период, описываемый рядом, абсолютный прирост (D) выразится как алгебраическая сумма частных приростов или, что очевидно, как разность между последним уровнем ряда и первым его уровнем:
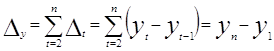 , где:
, где:
yn¾ последний уровень ряда;
у1¾ первый уровень.
Ускорение – это разность между последующим и предыдущим абсолютными приростами.
![]()
При расчете характеристики ускорения сопоставляемые временные отрезки должны быть одинаковы, а показатель может быть рассчитан только на основе цепных абсолютных приростов.
Темп роста (коэффициент роста) - отношение последующего уровня к предыдущему или какому-либо другому, принятому за базу сравнения. При помощи темпов роста измеряется, во сколько раз уровень текущего периода выше или ниже уровня базисного периода, или сколько процентов он составляет по отношению к базисному. Таким образом, темп роста может быть выражен в виде коэффициентов, когда определяется непосредственное отношение абсолютных размеров уровней, и в процентах, когда он показывает, сколько процентов текущий уровень составляет по отношению к базисному, принятому за 100%.
Темп роста в виде коэффициентов вычисляется по формулам:
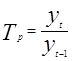 ¾ цепные темпы роста;
¾ цепные темпы роста;
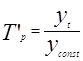 ¾ базисные темпы роста,
¾ базисные темпы роста,
где yconst – база сравнения;
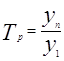 ¾ темп роста за весь период.
¾ темп роста за весь период.
Величина темпа роста больше единицы показывает увеличение уровня текущего периода по сравнению с базисным. Величина темпа роста, равная единице, показывает, что уровень текущего периода по сравнению с базисным не изменился, а величина темпа роста меньше единицы показывает уменьшение уровня текущего периода. Этот показатель характеризует интенсивность изменения уровня ряда.
Темпом прироста называется отношение абсолютного прироста к базисному уровню, т. е.
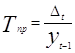 , где
, где
Dt ¾ абсолютный прирост данного уровня;
yt-1 и yconst — базисный уровень;
Tnp — темп прироста (в виде коэффициента).
Этот показатель характеризует относительную скорость изменения уровня ряда в единицу времени.
Поскольку абсолютный прирост (D) за весь период равен уп - у1, то темп прироста за весь период составит:
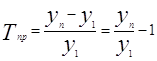 ,
,
где yn/y1 есть темп роста за этот период.
Тогда Тпр=Тр - 1, если темп роста и темп прироста выражаются в виде коэффициентов, и Тпр(%)=Тр(%) - 100, если они выражаются в процентах.
При темпах роста, меньших 100% или единицы (снижение уровней ряда), получаем отрицательные темпы прироста, т.е. темпы снижения.
Средний уровень динамического ряда
Чтобы найти средний уровень интервального ряда, достаточно сумму уровней этого ряда разделить на число периодов, к которым она относится, т.е.
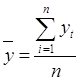
Средний абсолютный прирост
Обобщающим показателем скорости изменения явления во времени служит средний абсолютный прирост - средняя из абсолютных приростов за равные промежутки времени одного периода.
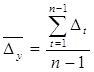
Средний темп роста
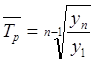
Средний темп прироста
Для расчета средних темпов прироста пользуются следующим соотношением:
![]() , (в виде коэффициентов)
, (в виде коэффициентов)
![]() .
.
Показатели динамического ряда объемов импорта США за период с 1977 по 2007 год представлены в Таблице 2, а экспорта в Таблице 3.
Таблица 2
Показатели изменений уровней динамического ряда объема импорта США за период с 1977 по 2006 гг.
| № п/п | год | Yt | ∆t | Tp | T'p | Tпр | T'пр |
| Уровень рядов динамики в момент t (исходные данные) | Абсолютный прирост ∆t = Yt - Yt-1 | Цепные темпы роста Tp = Yt/Yt-1 | Базисные темпы роста T'p = Yt/Yconst (Yconst = 1) | Темп прироста (цепной) Tпр = ∆t / Yt-1 | Темп прироста (базисный) T'пр = ∆t / Yconst | ||
| 1 | 1977 | 160,411 | 1.00 | ||||
| 2 | 1978 | 186,046 | 25,635 | 1,16 | 1,16 | 0,16 | 0,16 |
| 3 | 1979 | 222,225 | 36,179 | 1,19 | 1,39 | 0,19 | 0,23 |
| 4 | 1980 | 256,985 | 34,76 | 1,16 | 1,60 | 0,16 | 0,22 |
| 5 | 1981 | 273,352 | 16,367 | 1,06 | 1,70 | 0,06 | 0,10 |
| 6 | 1982 | 254,884 | -18,468 | 0,93 | 1,59 | -0,07 | -0,12 |
| 7 | 1983 | 269,878 | 14,994 | 1,06 | 1,68 | 0,06 | 0,09 |
| 8 | 1984 | 346,363 | 76,485 | 1,28 | 2,16 | 0,28 | 0,48 |
| 9 | 1985 | 352,463 | 6,1 | 1,02 | 2,20 | 0,02 | 0,04 |
| 10 | 1986 | 382,294 | 29,831 | 1,08 | 2,38 | 0,08 | 0,19 |
| 11 | 1987 | 424,443 | 42,149 | 1,11 | 2,65 | 0,11 | 0,26 |
| 12 | 1988 | 459,543 | 35,1 | 1,08 | 2,86 | 0,08 | 0,22 |
| 13 | 1989 | 492,922 | 33,379 | 1,07 | 3,07 | 0,07 | 0,21 |
| 14 | 1990 | 516,987 | 24,065 | 1,05 | 3,22 | 0,05 | 0,15 |
| 15 | 1991 | 508,363 | -8,624 | 0,98 | 3,17 | -0,02 | -0,05 |
| 16 | 1992 | 553,923 | 45,56 | 1,09 | 3,45 | 0,09 | 0,28 |
| 17 | 1993 | 603,438 | 49,515 | 1,09 | 3,76 | 0,09 | 0,31 |
| 18 | 1994 | 689,215 | 85,777 | 1,14 | 4,30 | 0,14 | 0,53 |
| 19 | 1995 | 770,852 | 81,637 | 1,12 | 4,81 | 0,12 | 0,51 |
| 20 | 1996 | 822,025 | 51,173 | 1,07 | 5,12 | 0,07 | 0,32 |
| 21 | 1997 | 899,020 | 76,995 | 1,09 | 5,60 | 0,09 | 0,48 |
| 22 | 1998 | 944,353 | 45,333 | 1,05 | 5,89 | 0,05 | 0,28 |
| 23 | 1999 | 1059,440 | 115,087 | 1,12 | 6,60 | 0,12 | 0,72 |
| 24 | 2000 | 1259,300 | 199,86 | 1,19 | 7,85 | 0,19 | 1,25 |
| 25 | 2001 | 1179,180 | -80,12 | 0,94 | 7,35 | -0,06 | -0,50 |
| 26 | 2002 | 1200,230 | 21,05 | 1,02 | 7,48 | 0,02 | 0,13 |
| 27 | 2003 | 1303,050 | 102,82 | 1,09 | 8,12 | 0,09 | 0,64 |
| 28 | 2004 | 1525,680 | 222,63 | 1,17 | 9,51 | 0,17 | 1,39 |
| 29 | 2005 | 1732,350 | 206,67 | 1,14 | 10,80 | 0,14 | 1,29 |
| 30 | 2006 | 1919,430 | 187,08 | 1,11 | 11,97 | 0,11 | 1,17 |
| 31 | 2007 | 2016,980 | 97,55 | 1,05 | 12,57 | 0,05 | 0,61 |
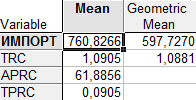
Таблица 3
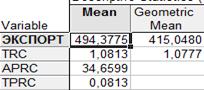
Показатели изменений уровней динамического ряда объема экспорта США за период с 1977 по 2007 гг.
| № п/п | год | Yt | ∆t | Tp | T'p | Tпр | T'пр |
| Уровень рядов динамики в момент t (исходные данные) | Абсолютный прирост ∆t = Yt - Yt-1 | Цепные темпы роста Tp = Yt/Yt-1 | Базисные темпы роста T'p = Yt/Yconst (Yconst = 1) | Темп прироста (цепной) Tпр = ∆t / Yt-1 | Темп прироста (базисный) T'пр = ∆t / Yconst | ||
| 1 | 1977 | 123,182 | 1,00 | ||||
| 2 | 1978 | 145,847 | 22,665 | 1,18 | 1,18 | 0,18 | 0,18 |
| 3 | 1979 | 186,363 | 40,516 | 1,28 | 1,51 | 0,28 | 0,33 |
| 4 | 1980 | 225,566 | 39,203 | 1,21 | 1,83 | 0,21 | 0,32 |
| 5 | 1981 | 238,715 | 13,149 | 1,06 | 1,94 | 0,06 | 0,11 |
| 6 | 1982 | 216,442 | -22,273 | 0,91 | 1,76 | -0,09 | -0,18 |
| 7 | 1983 | 205,639 | -10,803 | 0,95 | 1,67 | -0,05 | -0,09 |
| 8 | 1984 | 223,976 | 18,337 | 1,09 | 1,82 | 0,09 | 0,15 |
| 9 | 1985 | 218,815 | -5,161 | 0,98 | 1,78 | -0,02 | -0,04 |
| 10 | 1986 | 227,158 | 8,343 | 1,04 | 1,84 | 0,04 | 0,07 |
| 11 | 1987 | 254,122 | 26,964 | 1,12 | 2,06 | 0,12 | 0,22 |
| 12 | 1988 | 322,427 | 68,305 | 1,27 | 2,62 | 0,27 | 0,55 |
| 13 | 1989 | 363,812 | 41,385 | 1,13 | 2,95 | 0,13 | 0,34 |
| 14 | 1990 | 393,592 | 29,780 | 1,08 | 3,20 | 0,08 | 0,24 |
| 15 | 1991 | 421,730 | 28,138 | 1,07 | 3,42 | 0,07 | 0,23 |
| 16 | 1992 | 448,163 | 26,433 | 1,06 | 3,64 | 0,06 | 0,21 |
| 17 | 1993 | 464,773 | 16,610 | 1,04 | 3,77 | 0,04 | 0,13 |
| 18 | 1994 | 512,627 | 47,854 | 1,10 | 4,16 | 0,10 | 0,39 |
| 19 | 1995 | 584,743 | 72,116 | 1,14 | 4,75 | 0,14 | 0,59 |
| 20 | 1996 | 625,073 | 40,330 | 1,07 | 5,07 | 0,07 | 0,33 |
| 21 | 1997 | 689,182 | 64,109 | 1,10 | 5,59 | 0,10 | 0,52 |
| 22 | 1998 | 682,138 | -7,044 | 0,99 | 5,54 | -0,01 | -0,06 |
| 23 | 1999 | 695,797 | 13,659 | 1,02 | 5,65 | 0,02 | 0,11 |
| 24 | 2000 | 781,918 | 86,121 | 1,12 | 6,35 | 0,12 | 0,70 |
| 25 | 2001 | 729,100 | -52,818 | 0,93 | 5,92 | -0,07 | -0,43 |
| 26 | 2002 | 693,103 | -35,997 | 0,95 | 5,63 | -0,05 | -0,29 |
| 27 | 2003 | 724,771 | 31,668 | 1,05 | 5,88 | 0,05 | 0,26 |
| 28 | 2004 | 818,520 | 93,749 | 1,13 | 6,64 | 0,13 | 0,76 |
| 29 | 2005 | 907,158 | 88,638 | 1,11 | 7,36 | 0,11 | 0,72 |
| 30 | 2006 | 1038,270 | 131,112 | 1,14 | 8,43 | 0,14 | 1,06 |
| 31 | 2007 | 1162,98 | 124,71 | 1,12 | 9,44 | 0,12 | 1,01 |
Похожие работы
... в год увеличивался экспорт и импорт страны, какими темпами они росли, каковы были коэффициенты прироста и т. п. Поэтому представляется необходимым для более глубокого анализа динамики внешней торговли США в период 1993–1997 гг. рассчитать также производные показатели динамики. Ряды динамики – это ряды количественных характеристик изменения общественных явлений во времени, которые отображаются при ...
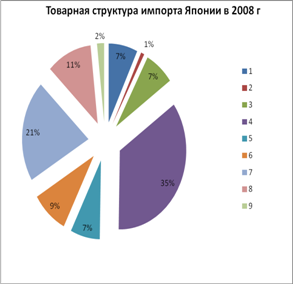
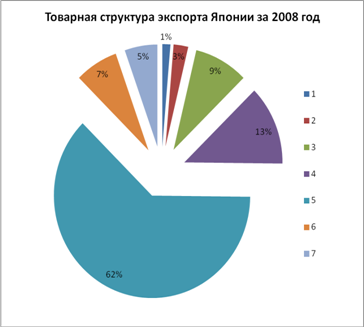
... стране были неблагоприятными. 2. Географическое распределение внешней торговли Японии за 2002–2010 годы Для полного анализа внешней торговли Японии не достаточно лишь рассмотреть динамику ее основных показателей, важно также понять географическую ориентацию внешнеэкономических связей страны. Для этого следует рассмотреть территориальную структуру внешней торговли Японии за 2 года (2002 ...
... ресурсов общества, что было характерно для деятельности многих предприятий в условиях социалистической экономики и, к сожалению, для деятельности некоторых предприятий в условиях переходной экономики. 1.3 Метод суммирования расходов Валовой внутренний продукт, подсчитанный по этому методу, представляет собой сумму расходов экономических агентов на все конечные товары и услуги: хлеб, яблоки, ...
... - - 59,49 138,65 90,82 Из стран ДЗ - - 16,29 122,09 44,59 Из стран СНГ - - 86,58 140,60 110,33 Заключение Данная работа состояла из 4 частей. Все вместе они представляли собой статистический анализ внешнеэкономической деятельности РФ. Но при этом каждая часть рассматривалась как ...
0 комментариев