Навигация
Аналитическое выравнивание динамического ряда
35563
знака
9
таблиц
76
изображений
2.2 Аналитическое выравнивание динамического ряда
Кривые роста, описывающие закономерности развития явлений во времени, получают путём аналитического выравнивания динамических рядов. Выравнивание ряда с помощью тех или иных функций (то есть их подгонка к данным) в большинстве случаев оказывается удобным средством описания эмпирических данных, характеризующих развитие во времени исследуемого явления. Это средство при соблюдении ряда условий можно применить и для прогнозирования. Процесс выравнивания состоит из следующих основных этапов:
выбора типа кривой, форма которой соответствует характеру изменения динамического ряда;
определения численных значений (оценивание) параметров кривой;
апостериорного контроля качества выбора тренда.
Найденная функция позволяет получить выровненные, или, как их иногда называют, теоретические значения уровней динамического ряда, то есть те уровни, которые наблюдались бы, если бы динамика явления полностью совпадала с кривой. Эта же функция с некоторой корректировкой или без неё, применяется и для экстраполяции.
Вопрос о выборе типа кривой является основным при выравнивании ряда. При всех прочих равных условиях ошибка в решении этого вопроса оказывается более значимой по своим последствиям (особенно для прогнозирования), чем ошибка, связанная со статистическим оцениванием параметров.
Весьма распространенным приемом выявления формы тренда является графическое изображение временного ряда. Но при этом весьма велико влияние субъективного фактора, даже при отображении выровненных уровней. Наиболее надежные методы выбора уравнения тренда основаны на свойствах различных кривых, применяемых при аналитическом выравнивании. Такой подход позволяет увязать тип тренда с теми или иными качественными свойствами развития явления.
Итак, рассмотрим следующие типы уравнений тренда:
линейная форма:
;
полином 2-ой степени:
;
полином 3-ей степени:
;
степенная форма:
;
экспоненциальная форма:
, или Yt = aebt
где 
- уровень ряда, полученный в результате выравнивания по прямой,
- начальный уровень тренда;
, 
, 
- константы тренда.
Это только часть тех кривых, которые можно было использовать для выравнивания ряда.
Задача: подобрать для каждого из периодов динамических рядов наилучший тренд, по которому будет спрогнозирован дальнейший результат.
Полученные уравнения трендов сведены в таблицы 2.49 – 2.54 по периодам и динамическим рядам с указанием значений остаточной дисперсии для каждой модели и коэффициента детерминации. Также был произведен выбор наилучших трендов, основанный на минимуме остаточной дисперсии и максимуме коэффициента детерминации.
Рассчитанные показатели представлены ниже.
Для их расчета будут использоваться следующие таблицы по периодам:
1 период:
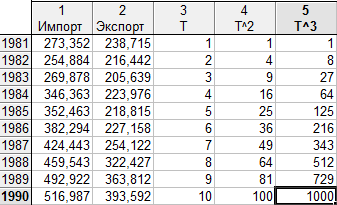
Рис. 10. Исходные данные
2 период:
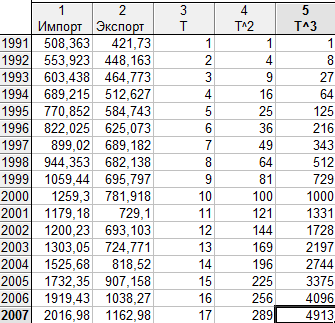
Рис. 11. Исходные данные
Где под Т подразумевается время.
Также нам потребуются следующие обозначения, которые используются в ППП Statistica:
в таблице «Результаты расчета параметров линейной модели тренда»
Estimate – числовые значения параметров уравнения;
Standard еrror – стандартная ошибка параметра;
t-value – расчетное значение t-критерия;
df – число степеней свободы (n-2);
p-level – расчетный уровень значимости;
Lo. Conf. Limit и Up. Conf. Limit – соответственно нижняя и верхняя граница доверительных интервалов для параметров уравнения с установленной вероятностью (указана как Level of Confidence в верхнем поле таблицы).
В таблице «Результаты дисперсионного анализа линейной модели тренда»:
В верхней заголовочной строке таблицы выдаются пять оценок:
Sum of Squares – сумма квадратов отклонений;
df – число степеней свободы;
Mean Squares – средний квадрат;
F-value – критерий Фишера;
p-value – расчетный уровень значимости F-критерия.
В левом столбце указывается источник вариации:
Regression – квадраты теоретических (полученных по тренда) значений признака;
Residual – отклонения фактических значений от теоретических (полученных по уравнению тренда);
Total – отклонения фактических значений 
от их средней величины.
На пересечении столбцов и строк получаем однозначно определенные показатели:
Regression / Sum of Squares – сумма квадратов прогнозных значений;
Residual / Sum of Squares – сумма квадратов отклонений теоретических и фактических значений (для расчета остаточной, необъясненной дисперсии);
Total / Sum of Squares – сумма первой и второй строчки (сумма квадратов фактических значений);
Corrected Total / Sum of Squares – сумма квадратов отклонений фактических значений от средней величины (для расчета общей дисперсии);
Regression vs. Corrected Total / Sum of Squares – повторение первой строчки;
Regression / Mean Squares – сумма квадратов прогнозных значений, деленная на число степеней свободы;
Residual / Mean Squares – остаточная, необъясненная дисперсия;
Regression vs. Corrected Total / Mean Squares – повторение первой строчки;
Regression / F-value – расчетное значение F-критерия.
В таблице «Таблица наблюдаемых, прогнозных значений и остатков для линейной модели тренда»:
Observed – наблюдаемые значения (то есть уровни исходного динамического ряда);
Predicted – прогнозные значения (полученные по уравнению тренда для данных моментов времени);
Residuals – остатки (разница между фактическими и прогнозными значениями).
1 период:
1.1. Линейная функция
1.1.1. Импорт
Model is: v1=a0+a1*v3
Dependent variable: Импорт Independent variables: 1
Loss function: least squares
Final value: 2860,58754087
Proportion of variance accounted for:,96459517 R =,98213806
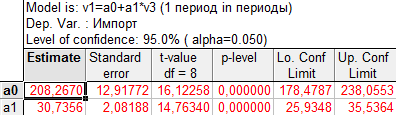
Рис. 12. Результаты расчета параметров линейной модели тренда
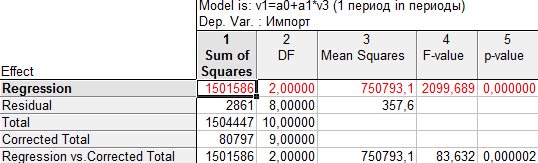
σ²ост = 357,6
Рис. 13. Результаты дисперсионного анализа линейной модели тренда
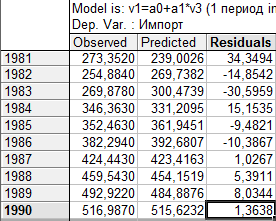
Рис. 14. Таблица наблюдаемых, прогнозных значений и остатков для линейной модели тренда
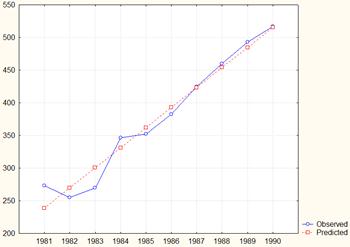
Рис. 15. Исходный динамический ряд и линейный тренд
Похожие работы
... в год увеличивался экспорт и импорт страны, какими темпами они росли, каковы были коэффициенты прироста и т. п. Поэтому представляется необходимым для более глубокого анализа динамики внешней торговли США в период 1993–1997 гг. рассчитать также производные показатели динамики. Ряды динамики – это ряды количественных характеристик изменения общественных явлений во времени, которые отображаются при ...
... стране были неблагоприятными. 2. Географическое распределение внешней торговли Японии за 2002–2010 годы Для полного анализа внешней торговли Японии не достаточно лишь рассмотреть динамику ее основных показателей, важно также понять географическую ориентацию внешнеэкономических связей страны. Для этого следует рассмотреть территориальную структуру внешней торговли Японии за 2 года (2002 ...
... ресурсов общества, что было характерно для деятельности многих предприятий в условиях социалистической экономики и, к сожалению, для деятельности некоторых предприятий в условиях переходной экономики. 1.3 Метод суммирования расходов Валовой внутренний продукт, подсчитанный по этому методу, представляет собой сумму расходов экономических агентов на все конечные товары и услуги: хлеб, яблоки, ...
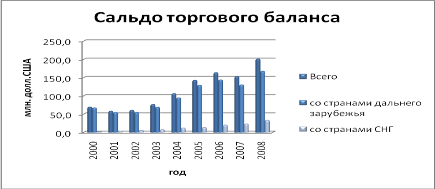
... - - 59,49 138,65 90,82 Из стран ДЗ - - 16,29 122,09 44,59 Из стран СНГ - - 86,58 140,60 110,33 Заключение Данная работа состояла из 4 частей. Все вместе они представляли собой статистический анализ внешнеэкономической деятельности РФ. Но при этом каждая часть рассматривалась как ...
0 комментариев