Місце стереометричного матеріалу в курсі математики основної школи та вимоги до його засвоєння

1.2.2 Місце стереометричного матеріалу в курсі математики основної школи та вимоги до його засвоєння

Структурування навчального матеріалу з геометрії доцільно здійснити на основі таких принципів:

а) у курсі математики в 5–6-х класах треба ознайомити учнів з основними поняттями геометрії площини та простору на наочно-інтуїтивному та оперативному рівнях, формулами для обчислення площ поверхонь та об’ємів геометричних тіл, готувати учнів до вивчення систематичного курсу геометрії, суміжних дисциплін;

б) систематичне вивчення геометрії має починатися з 7-го класу курсом планіметрії, який містить дещо розширену порівняно з 5–6-м класами стереометричну частину;

в) стереометричний матеріал має органічно поєднуватися з аналогічним планіметричним матеріалом; властивості плоских фігур треба демонструвати на відповідних елементах стереометричних фігур, розкриваючи тим самим певні властивості останніх;

г) вивчення стереометричного матеріалу в основній школі має носити практичний характер, базуватися переважно на дослідах, інтуїції, експерименті; тим самим буде сформовано необхідний запас просторових уявлень як основи для вивчення систематичного курсу стереометрії в 10–11-х класах на науково-теоретичному рівні;

ґ) курс планіметрії треба завершити узагальнюючим розділом «Елементи стереометрії».

Уявлення про місце стереометричного матеріалу в курсі математики основної школи та його структурування дає таблиця 3 (див. додаток В).

Передбачається вивчення геометричного матеріалу з різним ступенем обґрунтованості та повноти. Мінімальний рівень підготовки описаний за допомогою завдань відповідно до класу та навчального матеріалу.

Обовязкові результати навчання

5–6-й класи

1. Точка, пряма, площина, промінь, відрізок.

1. Позначте точку і проведіть через неї три прямі.

2. Проведіть пряму і позначте на ній точки A, B, C. Назвіть відрізки, що утворилися.

3. Розгляньте рис. 1.

 

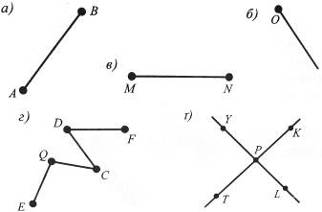
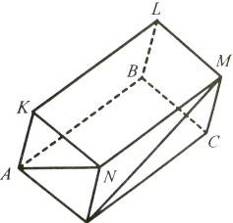
Рис. 1 Рис. 2

Які фігури зображено на ньому? Назвіть: три відрізки; три промені. Скільки прямих зображено на рисунку?

6. Назвіть відрізки і точки, зображені на рисунку прямокутного паралелепіпеда (рис. 2).

2. Довжина відрізка.

1. Накресліть пряму і позначте на ній точки A та B. Виміряйте відрізок АВ. Запишіть, чому дорівнює його довжина.

2. Накресліть відрізки AB та BC, якщо AB=5 см, BC=4 см 3 мм.

3. Виберіть серед запропонованих моделей модель куба. Виміряйте та запишіть довжину його ребра в сантиметрах (з точністю до десятих).

4. Виміряйте та запишіть довжини ребер сірникової коробки в сантиметрах (з точністю до десятих).

3. Кут та його елементи. Види кутів.

1. Позначте точку О. Проведіть промені ОА та ОВ. Яка фігура утворилася? Назвіть її елементи.

2. Серед оточуючих предметів назвіть ті, які містять прямий кут.

3. На рис. 3 зображено кути. Назвіть:

а) гострі кути;

б) прямі кути;

в) тупі кути; Рис. 3

г) розгорнуті кути.

4. Побудуйте прямий, гострий і тупий кути. Який з цих кутів найбільший (найменший)?

5. За допомогою косинця накресліть дві прямі, які при перетині утворюють прямі кути. На скільки частин вони ділять площину? Скільки розгорнутих кутів на рисунку?

4. Міра кута.

1. Виміряйте кути, зображені на рис. 3; запишіть результати вимірювань.

2. Накресліть кут, градусна міра якого: а) 65°; б) 115°.

3. Які з кутів гострі, а які тупі, якщо = 67°, =175°, =92°, =3°?

5. Паралельні та перпендикулярні прямі.

1. На рис. 4 зображено прямі. Які з них:

а) перетинаються; б) перпендикулярні; в) паралельні?

 

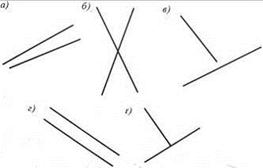
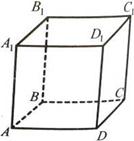
Рис. 4 Рис. 5

2. На оточуючих предметах назвіть (покажіть) елементи, які містять паралельні та перпендикулярні прямі.

3. Накресліть пряму. Поза прямою позначте точку та проведіть через неї за допомогою косинця пряму, перпендикулярну до даної прямої.

4. Назвіть у кубі, зображеному на рис. 5:

а) відрізки паралельних прямих;

б) відрізки перпендикулярних прямих.

6. Трикутник і його елементи.

1. Накресліть трикутник. Назвіть вершини, сторони, кути трикутника.

2. Назвіть трикутники, зображені на рис. 6.

 

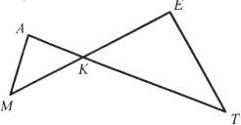
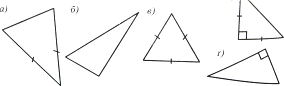
Рис. 6 Рис. 7

3. Назвіть кілька предметів, що вас оточують, які мають форму трикутника.

4. Накресліть прямокутний, гострокутний, тупокутний трикутники.

5. Накресліть рівносторонній, рівнобедрений, рівносторонній трикутники.

6. Серед трикутників, зображених на рис. 7, назвіть:

а) гострокутні, прямокутні, тупокутні;

б) різносторонні, рівнобедрені, рівносторонні.

7. Накресліть гострокутний, прямокутний і тупокутний трикутники та проведіть усі їх висоти.

8. Накресліть довільний трикутник і виміряйте його кути. Знайдіть суму цих кутів.

7. Чотирикутники. Види чотирикутників. Прямокутник, квадрат, паралелограм, ромб. Висота паралелограма.

1. Які із зображених на рис. 8 фігур мають форму чотирикутника?

 

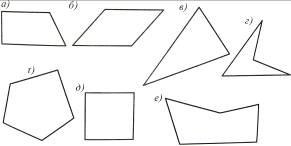
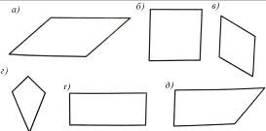
Рис. 8 Рис. 9

2. Серед зображених на рис. 9 фігур назвіть: а) прямокутник; б) паралелограм.

3. Назвіть кілька предметів, що мають форму прямокутника, квадрата.

4. Накресліть за допомогою косинця та лінійки паралелограм ABCD. За допомогою косинця проведіть його висоти з вершини A до сторони CD та з вершини B до сторони AC.

8. Коло. Круг. Кругові діаграми.

1.  Накресліть коло. Позначте точкою О його центр. Проведіть радіуси ОА та ОВ. Як називають частину кола між точками A та B? Як називають частину круга між радіусами ОА та ОВ?

2.  Назвіть кілька предметів, що мають форму: а) кола; б) круга.

3.  За допомогою циркуля накресліть коло радіусом 3 см. Проведіть діаметр цього кола. Яка його довжина?

9. Довжина кола. Число .

1.  Обчисліть довжину кола, радіус якого 2,5 см, вважаючи, що 3,14. Результат округліть до десятих.

2.  Накресліть довільне коло. Виміряйте його радіус і обчисліть довжину кола.

3.  Довжина діаметра земного екватора дорівнює 12756 км. Знайдіть довжину екватора, якщо 3,14. Відповідь округліть до десятків кілометрів.

10. Прямі призми: прямокутний паралелепіпед, куб, трикутна призма, прямий паралелепіпед.

1. Серед моделей геометричних тіл знайдіть:

а) прямий паралелепіпед; б) трикутну призму.

2. Серед оточуючих предметів назвіть ті, що мають форму прямокутного паралелепіпеда. Скільки граней має прямокутний паралелепіпед?

3. Серед оточуючих предметів назвіть ті, що мають форму прямої трикутної призми.

4. Виготовіть за готовими розгортками (рис. 10) відповідні фігури.

5.

 

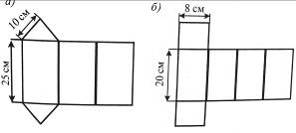
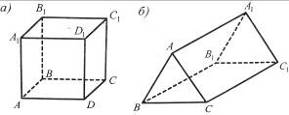
Рис. 10 Рис. 11

6. Які фігури зображено на рис. 11?

11. Піраміда та її елементи.

1.  Серед даних моделей пірамід знайдіть:

а) трикутні піраміди; б) чотирикутні піраміди.

2.  Які геометричні фігури є бічними гранями піраміди?

3.  Скільки бічних граней має трикутна, чотирикутна, п'ятикутна піраміди?

5. Дано модель піраміди. Покажіть:

а) основу піраміди;

б) бічні грані піраміди;

в) вершину піраміди.

6. Яку фігуру зображено на рис. 12? Назвіть:

а) основу зображеної фігури;

б) вершину зображеної фігури;

в) бічні грані цієї фігури;

г) її бічні ребра.

12. Циліндр, конус, куля та їх елементи.

1.  Серед даних моделей знайдіть: а) циліндр; б) конус; в) кулю.

2.  Назвіть кілька предметів, що мають форму: а) циліндра; б) конуса; в) кулі.

3. Розгляньте модель циліндра. Що є його основами? Яка фігура є бічною поверхнею циліндра?

4. На моделі конуса покажіть його основу, вершину, бічну поверхню.

5. Яку фігуру зображено на рис. 13? Назвіть:

а) основи фігури; б) її твірну.

6. Назвіть основу, вершину, висоту, твірну зображеної на рис. 14 фігури.

  

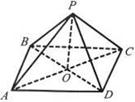
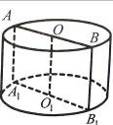
Рис. 12 Рис. 13 Рис. 14

7. Серед даних розгорток (рис. 15) знайдіть: а) розгортку циліндра; б) розгортку конуса.

Рис. 15

 

13. Площа. Одиниці вимірювання площі.

1. Площа одного квадрата, зображеного на рис. 16, дорівнює 1 см². Яка площа кожної фігури, зображеної на рисунку?

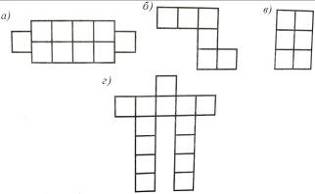
Рис. 16

2. На прямокутній ділянці зі сторонами 110 м і 75 м скосили траву. З якої площі скошено траву?

3.  Знайдіть площу паралелограма з основою 16 дм і висотою 7 дм, опущеною на цю основу.

4.  Знайдіть площу круга радіуса 54 см, вважаючи, що 3,14. Результат округліть до десятих.

5.  Діаметр арени цирку 13,6 м. Яку площу має арена цирку (3,14)? Результат округліть до одиниць.

14. Об'єм. Одиниці вимірювання об'єму.

1. Фігури на рис. 17 складені з кубів, об'єм кожного з яких 1 см³. Знайдіть об’єм кожної фігури.

Рис. 17

2. Знайдіть об'єм прямокутного паралелепіпеда, якщо його виміри дорівнюють 7 см, 4 см, 3 см.

3.  Виміряйте на моделі прямокутного паралелепіпеда його довжину, ширину та висоту. Обчисліть його об'єм.

4.  Знайдіть об'єм кімнати, якщо її довжина 5 м, ширина 4 м, висота 3 м.

5.  Знайдіть об'єм ями, що має форму куба, якщо її глибина 3 м.

6.  Знайдіть об'єм призми, основою якої є прямокутний трикутник з катетами 5 дм і 6 дм. Висота призми дорівнює 8,5 дм.

7.  Обчисліть об'єм піраміди, основою якої є квадрат зі стороною 7 см. Висота піраміди 11 см.

8.  Знайдіть об'єм труби, що має форму циліндра, якщо її радіус 3 дм, а довжина 50 дм.

9.  Знайдіть об'єм води, що вміщує лійка у вигляді конуса, якщо її діаметр 40 см, а висота 30 см.

10. Знайдіть об'єм кулі, радіус якої 8 см.

15. Поверхня геометричного тіла. Площа поверхні геометричного тіла.

1. Знайдіть площу поверхні куба, якщо довжина його ребра дорівнює 8 см.

2. Основою прямої призми є рівносторонній трикутник зі стороною 8 см; висота призми 13 см. Знайдіть площу бічної поверхні призми.

3. Скільки потрібно жерсті, щоб покрити дах у вигляді піраміди, основою якої є квадрат зі стороною 7 м, а висота її бічної грані 4 м?

4. Знайдіть площу повної поверхні циліндра, радіус основи якого дорівнює 5 см, а висота 14 см.

5.  Знайдіть площу повної поверхні конуса, якщо висота конуса 18 см, а радіус основи 5 см.

6.  Знайдіть площу поверхні кулі, радіус якої 8 см.

7–9-й класи

Елементи стереометрії

1. Прямі на площині та в просторі. Паралельність і перпендикулярність прямих на площині та в просторі.

1. На моделі прямокутного паралелепіпеда (або на його зображенні) покажіть по дві пари:

а) паралельних прямих; б) перпендикулярних прямих; в) мимобіжних прямих.

2. На каркасній моделі піраміди покажіть прямі, шо не перетинаються.

3. На моделі трикутної піраміди покажіть:

а) дві мимобіжні прямі; б) дві прямі, що перетинаються.

4. На зображенні прямої призми покажіть:

а) дві паралельні прямі; б) дві перпендикулярні прямі; в) дві мимобіжні прямі.

5. На зображенні чотирикутної піраміди покажіть дві мимобіжні прямі.

6. На зображенні куба покажіть дві прямі, паралельні третій.

2. Рівність трикутників.

1.На зображенні трикутної призми назвіть і покажіть рівні трикутники.

2.Основою піраміди PABCD є прямокутник ABCD. ЇЇ бічні ребра РА, РВ, PC, PD рівні. Для кожної її трикутної грані назвіть рівну їй грань.

3.У чотирикутній піраміді SABCD всі ребра рівні. Встановіть вид трикутників SAB, SAC, BSD.

4.У призмі ABCA₁B₁C₁ бічні грані ABB₁A₁ та ВСС₁В₁ рівні. Доведіть, що в трикутнику ABC, який є основою призми, кути А та С рівні.

3. Коло.

1. На моделі або зображенні циліндра покажіть коло, його центр, радіус.

2. На зображенні конуса проведіть діаметр та хорду кола основи.

3. На каркасній моделі кулі покажіть її центр, радіус, діаметр.

4. Чотирикутники.

1. На моделі прямої призми, основою якої є паралелограм, покажіть рівні грані.

2. Основою прямої призми є ромб. Доведіть, що її бічні грані – рівні прямокутники.

3. На моделі прямої призми, основою якої є рівнобічна трапеції, покажіть:

а) рівні бічні грані; б) паралельні прямі; в) перпендикулярні прямі.

4.  На зображенні піраміди, основою якої є прямокутник, проведіть діагоналі основи та позначте точку їх перетину.

5.  Основою піраміди є прямокутник. Бічні ребра піраміди рівні. Доведіть рівність трикутників, що містять вершину піраміди та діагоналі основи.

5. Теорема Піфагора.

1. Ребро куба дорівнює a. Знайдіть довжину діагоналі його грані.

2. Ребро куба дорівнює a. Знайдіть довжину його діагоналі.

3. Дано зображення прямокутного паралелепіпеда. Знайдіть довжини діагоналей паралелепіпеда, якщо довжини трьох ребер, що виходять з однієї вершини, дорівнюють 2 дм, 3 дм, 6 дм.

4. Обчисліть діагональ бічної грані прямої призми, основою якої є ромб зі стороною 6 см, а бічне ребро дорівнює 8 см.

5. Обчисліть висоту бічної грані піраміди, основою якої є квадрат зі стороною 10 см. Довжина кожного бічного ребра 13 см.

6. Розв'язування трикутників.

1.  Основа прямого паралелепіпеда – ромб зі стороною 6 см і кутом 60°. Висота паралелепіпеда дорівнює 8 см. За готовим зображенням знайдіть довжину меншої діагоналі паралелепіпеда.

2.  За готовим зображенням обчисліть діагоналі прямої призми, основою якої є паралелограм зі сторонами 2 см і 3 см та гострим кутом 45°. Висота призми 4 см.

3.  Основою піраміди SABCD є прямокутник ABCD. O – точка перетину його діагоналей; 50 – висота піраміди. Обчисліть довжину бічного ребра піраміди, якщо її висота дорівнює 14 см, а кут між діагоналлю основи та бічним ребром 60°. Скористайтесь готовим рисунком.

4.  Висота прямої призми, основою якої є квадрат, дорівнює h, а діагональ призми утворює з діагоналлю основи кут . Знайдіть:

а) діагональ призми; б) діагональ основи призми.

5. Діагональ осьового перерізу циліндра d нахилена до площини його основи під кутом . Знайдіть: а) висоту циліндра; б) діаметр основи.

7. Прямі та площини в просторі.

1. На моделі прямої трикутної призми покажіть:

а) паралельні пряму та площину; б) перпендикулярні площини.

2.  На моделі трикутної піраміди покажіть дві площини, що перетинаються.

3.  Зобразіть площину , що проходить через пряму b.

4.  Зобразіть площину і пряму с, які перетинаються у точці N.

5.  Зобразіть площини  та , що перетинаються по прямій m.

8. Многогранники. Тіла обертання.

1. Накресліть прямокутний паралелепіпед. Зобразіть діагоналі основи.

2. Накресліть многогранник, який має 4 грані. Скільки він має ребер, вершин?

3. Накресліть циліндр. Зобразіть його висоту, твірну.

4. Висота циліндра дорівнює 6 см, а радіус його основи 5 см. Знайдіть площу осьового перерізу.

5. Обчисліть діагональ осьового перерізу циліндра, твірна якого дорівнює 3,5 см, а радіус основи 2 см.

6. Накресліть конус. Зобразіть його висоту, твірну. Покажіть його вершину, основу.

7. Обчисліть площу осьового перерізу конуса, радіус основи якого дорівнює 15 мм, а твірна 30 мм.

8. Накресліть кулю. Зобразіть її радіус. Зобразіть переріз кулі площиною. Яка фігура утворилася в перерізі?

9. У кулі радіуса 26 см на відстані 10 см від центра проведено січну площину. Знайдіть площу перерізу.

9. Об'єм і поверхня геометричного тіла.

1. Знайдіть площу поверхні прямокутного паралелепіпеда, у якого діагональ дорівнює 13 дм, висота 12 дм, а одне з ребер основи 4 дм.

2. Основою прямої призми є трикутник, у якого сторони довжиною 5 см і 6 см утворюють кут 30°. Бічне ребро призми дорівнює 4 см. Знайдіть об'єм призми.

3. У прямій призмі основа – прямокутний трикутник з катетами 6 см і 8 см. Бічне ребро призми дорівнює 12 см. Знайдіть площу повної поверхні призми.

4. Знайдіть площу поверхні піраміди, основою якої є квадрат. Кожне ребро піраміди дорівнює 3 дм.

5. Сторони прямокутника дорівнюють 4 см і 5 см. Знайдіть площу повної поверхні тіла, утвореного обертанням цього прямокутника навколо меншої сторони.

6. Осьовий переріз циліндра – прямокутник зі сторонами 12 см і 26 см. Знайдіть об'єм циліндра, якщо його висота дорівнює меншій стороні осьового перерізу.

7. Твірна та радіус основи конуса дорівнюють відповідно 5 м і 2 м. Знайдіть площу поверхні конуса.

8. Покрівля силосної башти має форму конуса. Висота покрівлі 2 м, діаметр башти 6 м. Знайдіть площу поверхні покрівлі.

2. Методичні основи вивчення елементів стереометрії у курсі геометрії 9 класу

 

2.1 Аналіз змісту і методів вивчення елементів стереометрії у курсі геометрії 9 класу за новими підручниками з геометрії

У зв'язку з введенням у школах нових навчальних планів і програм з математики постала гостра потреба у підручниках, які б відповідали вимогам нових програм.

Навчання математики у 9 класах загальноосвітніх навчальних закладів здійснюється за новими підручниками: «Геометрія. 9 клас» (автори А.Г. Мерзляк, В.Б. Полонський, М.С. Якір) видавництва «Гімназія», «Геометрія. 9 клас» (автори Бурда М.І., Тарасенкова Н.А.) видавництва «Зодіак – ЕКО», «Геометрія. 9 клас» (автори А.П. Єршова, В.В. Голобородько, О.Ф. Крижановський, С.В. Єршова) видавництва «Ранок».

Ці підручники створено відповідно до Державного стандарту та нових програм з алгебри та геометрії для 9 класу загальноосвітніх навчальних закладів. Однією з основних проблем шкільних підручників геометрії – оптимальне поєднання науковості й доступності викладення матеріалу. Складністю вирішення цієї проблеми пояснюється те, що українські школи мають обмаль підручників, за якими справді хотілося б навчати учнів. Та з іншого боку, це дало поштовх до педагогічної творчості чималій кількості небайдужих вчителів.

Розглянемо, як висвітлений розділ «Початкові відомості зі стереометрії» у цих підручниках.

У підручнику «Геометрія, 9» М.І. Бурди, Н.А. Тарасенкової розділ розпочинається переліком передбачуваних пізнавальних результатів («У розділі дізнаєтесь…»), а завершується рубрикою «Перевірте, як засвоїли матеріал розділу». Тут подано контрольні запитання узагальнюючого характеру і тестові завдання. У кожному параграфі є: основний навчальний матеріал; додаткові відомості (рубрика «Дізнайтеся більше»); запитання для повторення вивченого (рубрика «Згадайте головне»); система задач, диференційована за складністю (рубрика «Розв'яжіть задачі»), яку завершує окремий блок завдань «Застосуйте на практиці».

Науковість змісту розділу забезпечена в першу чергу логічно послідовним розміщенням навчального матеріалу, коректним формулюванням означень понять, достатнім рівнем строгості. Логічне упорядкування і послідовність навчального матеріалу розділу відповідають вимогам дидактики і математики як науки. Термінологія сучасна, предметна й однозначна. Поняття і властивості геометричних фігур сформульовані коректною математичною мовою. Чітко розмежовується зміст понять (перераховуються всі суттєві ознаки) і їх обсяг (вказується множина об'єктів, де застосовується поняття). При цьому зміст понять розкривається за допомогою означень, а їх обсяг – із залученням класифікацій (поділу понять за певною ознакою). З одного боку, це покращить засвоєння і застосування понятійного апарату даної теми, а з другого – посилить його зорове сприймання. Заслуговує на увагу і те, що поряд з означеннями понять через найближчий рід і видову відмінність, сприймання яких вимагає складнішої розумової діяльності, використовуються і конструктивні означення, які дають змогу учневі усвідомити сам процес створення (побудови) відповідного стереометричного об’єкта. Тому означення поняття нерідко спирається або на малюнок, або побудову відповідної геометричної фігури, або на розгляд життєвої ситуації. Учням пропонується спочатку самостійно дати означення поняттю, а потім порівняти його з наведеним у підручнику.

Вивчення геометричних фактів, як правило, розпочинається з аналізу учнем емпіричного досвіду (відповідних прикладів із довкілля, моделей чи малюнків), або з опису практичних дій. Це дає змогу проводити невеликі дослідження, з'ясовувати суттєві ознаки понять, властивості геометричних фігур і на основі цього самостійно формулювати відповідні твердження. Самостійно оволодіти навчальним матеріалом допоможе і підкріплення його малюнками, які виконують не лише ілюстративну, а й евристичну роль – на малюнках кольором виділено дані і шукані величини, допоміжні побудови тощо. Кольорові фотографії та ілюстрації також несуть ретельно продумане дидактичне навантаження.

Задачі підручника мають чотири рівні складності – початковий, середній, достатній і високий. Усередині набору кожного рівня складності задачі згруповані за порядком вивчення теоретичних відомостей. Як правило, набори початкового і середнього рівнів складності розпочинаються із задач за готовими малюнками. Хоча вони не є винятком і серед більш складних задач. Окремі найбільш важливі задачі-теореми виділені чорним шрифтом. Учням доцільно запам’ятати їх формулювання. Ці геометричні твердження можна застосовувати у розв'язуванні інших задач. Особливістю задач є те, що задачі високого рівня складності включають елементи задач середнього і достатнього рівнів, а останній – елементи задач початкового рівня.

Особливістю розділу є прикладна спрямованість змісту. Автори намагалися, де це можливо, не лише показати виникнення геометричного факту із практичної ситуації, а й проілюструвати застосування його на практиці. З цією метою в окремо виділеному блоці завдань «Застосуйте на практиці» подано типові практичні ситуації, де потрібно застосувати вивчений матеріал.

У підручнику «Геометрія, 9» А.П.Єршової, В.В. Голобородько, О.Ф. Крижановського, С.В.Єршова зазначено, що цей розділ «своєрідний стислий огляд курсу геометрії 10–12 класів». Тема «Початкові відомості зі стереометрії» передбачає ознайомлення учнів з фігурами в просторі і є пропедевтичним вступом до курсу стереометрії, що вивчатиметься у старших класах. Разом із цим, у порівнянні з попередніми підручниками, з'являються нові дидактичні акценти, пов'язані зі специфікою «геометрії методів», розширюються і поглиблюються окремі питання щодо властивостей геометричних фігур, методики розв'язування задач тощо.

Структура, обсяг і співвідносність розділів навчального матеріалу повністю відповідають діючій програмі. Однак порівняно з традиційними підходами до розгляду відповідного навчального матеріалу запропоновано декілька важливих інновацій. Це дає можливість спростити низку доведень. Найбільш складні з точки зору обґрунтування теореми супроводжуються в основному тексті зрозумілими для пересічного учня загальними схемами міркувань, а відповідні строгі доведення подаються в «Додатках».

У тексті виділено основний зміст (означення, теореми й наслідки з них), доповнення та приклади розв'язування задач. До кожної теореми подано її назву. Наприкінці розділу міститься підсумковий огляд його змісту у вигляді таблиці, які наочно ілюструють змістовно-логічні та структурно-функціональні зв'язки між елементами навчального матеріалу.

Крім того, наприкінці розділу пропонуються контрольні запитання і типові задачі для підготовки до контрольної роботи. Наявність цих матеріалів дає змогу учневі самостійно оцінити рівень своєї математичної підготовки; запитання і задачі мають діагностичну цінність і сприяють корекції знань. Додаткові задачі до розділу призначені для організації інтегрованого повторення і узагальнення вивченої теми, встановлення внутрішніх взаємозв'язків між окремими фрагментами теми. Окремо після розділу виділено задачі підвищеної складності. Така організація матеріалу дає змогу забезпечити опанування учнем програмового змісту як під керівництвом учителя, так і самостійно.

Теоретичний матеріал побудовано за схемою «означення основних понять – аксіоми й теореми – наслідки – приклади застосування». Окреме місце відводиться опорним задачам, які містять додаткові теоретичні відомості, на які учні далі можуть посилатися без доведення. Такі задачі подаються як в основному тексті параграфів, так і в задачному матеріалі. Задачі до кожного параграфа розподілено на чотири групи. Першу групу складають усні вправи – завдання теоретичного плану, розгляд яких є проміжним етапом між вивченням теорії і розв'язуванням письмових задач. Наявність таких задач дає змогу використовувати на уроці інтерактивні форми роботи. Друга група завдань – графічні вправи, які учні можуть виконувати як власноруч у зошиті, так і за допомогою комп'ютера. Ці вправи дають наочне уявлення про базові геометричні конфігурації, що вивчаються, сприяють розвитку початкових креслярських умінь і навичок роботи з графічними комп'ютерними програмами. Наступну групу складають письмові задачі, згруповані за трьома рівнями складності. Зазначимо, що на кожному рівні завдання диференційовано за змістом навчальної діяльності – задачі на обчислення, доведення, побудову тощо. Нарешті, наприкінці кожного параграфа виділено теоретичний матеріал, який необхідно повторити для свідомого засвоєння наступної теми, і подано задачі для повторення.

Розв'язувати всі задачі розділу не обов'язково (а з урахуванням наявного навчального часу і неможливо). Задачі до кожної теми свідомо подано в надлишковій кількості, щоб розширити творчі можливості вчителя, сприяти організації особистісно-орієнтованого навчання, диференціації роботи учнів у класі та вдома з урахуванням їхніх індивідуальних можливостей і рівня математичної підготовки.

До теми «Взаємне розташування прямих у просторі» у трьох підручниках докладно подано основні фігури в просторі, позначення і зображення площин, розміщення точок у просторі. У підучниках Мерзляка і Єршова чітко виділені твердження, як однозначно задати площину. Також тут подані графічні зображення взаємного розміщення двох прямих у просторі, у підручнику Бурди лише продемонстровано на прикладі кімнати.

До теми «Взаємне розміщення прямих і площин у просторі» у підручнику Бурди всі випадки взаємного розміщення прямої і площини, двох площин наведені в таблиці, графічних зображень немає.

При вивченні в 9 класі даного розділу значну увагу слід приділити формуванню в учнів культури графічного зображення просторових тіл та їх елементів. До даних тем у трьох підручниках вдало підібрані усні та графічні вправи, у підручниках Мерзляка, Бурди значна увага приділена задачам практичного змісту, більшість задач супроводжуються допоміжними малюнками. Таким чином, вивчаючи перші теми стереометрії учні відзначають, що в просторі взаємне розташування фігур є більш різноманітним, ніж у площині.

Наступні теми передбачають вивчення основних тіл стереометрії, вони закладають формування переходу від мислення в категоріях плоских фігур до мислення в просторі, також усвідомлення того, що для визначення взаємного розташування фігур у просторі слід правильно виокремити ті елементи, які визначають це взаємне розташування.

Так, до теми «Поняття многогранника. Призма.» у даних підручниках сформульоване поняття геометричного тіла, многогранника та його елементів, наведені наочні та графічні зображення призм. Дев’ятикласники вже мають запас просторових уявлень, тому при вивченні даних тем вони доповнюються і систематизуються.

У підручниках Мерзляка і Єршова подається доведення теорем про площу бічної поверхні прямої призми.

У підручнику Бурди вивчення піраміди і призми подано одночасно, властивості розглядаються без доведень, проте вони мають достатньо переконливе наочне підтвердження. Так, вивчення властивостей фігур у просторі спирається на приклади з довкілля, макети, малюнки або досліди. Щоб учні до формул об’ємів призми (піраміди) розглядаються досліди з пересипанням піску.

Циліндр, конус, куля подаються в усіх підручниках як тіла обертання. Бічні поверхні циліндра і конуса розглядаються через розгортки відповідно циліндра і конуса.

На мою думку, те, що у підручнику Бурди призма і піраміда подаються разом є своєрідним недоліком. Також сюди можна віднести той факт, що ми бачимо перенасичення задачами. Слід зазначити, що не всі задачі однаковою мірою сприяють цілеспрямованому розвитку даного процесу. Саме тому доцільно використовувати систему вправ і задач, яку будують так, щоб учень самостійно застосовував свої знання, вміння, уявлення, щоб у нього вироблялася звичка переносити знання у нові ситуації. Розв’язуючи задачі учні повинні усвідомлювати ті дії, які вони при цьому виконують. Аналіз дій дає їм змогу підходити до пошуків алгоритмів розв’язання задач певного виду, а потім і до алгоритмізації більш складних видів навчальної діяльності.

У школі вчителі протягом вивчення стереометрії приділяють увагу в основному опрацюванню теорії та розв’язуванню абстрактних задач, оскільки вони недооцінюють можливості реалізації прикладної спрямованості для досягнення цілей вивчення цього курсу. Посилюють цю ситуацію такі фактори: невелика кількість годин, що відведена для вивчення курсу стереометрії; у методичній літературі мало матеріалів, які доводять значущість прикладної спрямованості та конкретних методичних розробок, що допомагають вчителю ефективно використовувати її засоби тощо. З огляду на перераховані обставини, у вчителів відсутня мотивація для систематичного прикладного спрямування курсу, зокрема для розв’язування з учнями прикладних задач, особливо враховуючи їх невелику кількість у підручниках, посібниках та майже повну відсутність серед добірок завдань контролюючого характеру.