Роль і місце елементів стереометрії у розвитку просторового мислення школярів
Місце стереометричного матеріалу в курсі математики основної школи та вимоги до його засвоєння
Загальні методичні рекомендації вивчення елементів стереометрії у курсі геометрії 9 класу
Система вправ для формування початкових стереометричних знань і методика їх розв’язування
Зобразіть конус. Побудуйте на зображенні діаметр основи
Практична реалізація вивчення стереометричного матеріалу у 9 класі з використанням інформаційних технологій
Створення моделей просторових об’єктів
Обчислення значення вираження
Навигация
Система вправ для формування початкових стереометричних знань і методика їх розв’язування
Вивчення елементів стереометрії у курсі геометрії 9 класу
111254
знака
0
таблиц
31
изображение
2.2.2 Система вправ для формування початкових стереометричних знань і методика їх розв’язування
Усі психічні процеси, зокрема просторова уява, формуються і удосконалюються в результаті діяльності. Таку діяльність необхідно стимулювати й координувати в процесі навчання математики через розв'язування задач. Запропонована нами система вправ має за мету формувати в учнів просторові уявлення, готувати їх до сприйняття стереометричного матеріалу в 10–11-х класах.
Вона включає вправи трьох типів на формування:
1)просторових уявлень та уяви учнів;
2)вимірювальних та обчислювальних навичок;
3)конструктивних навичок.
Належну увагу необхідно приділити формуванню навичок оперування просторовими уявленнями, одержаними в результаті попередньої діяльності. При цьому як засіб наочності разом з моделями геометричних тіл доцільно використовувати їх зображення. Уміння бачити просторові образи на готовому кресленні є важливим стимулом для розвитку просторових уявлень та уяви. У результаті виконання відповідних вправ образи поступово втрачають індивідуальні ознаки, набувають абстрактнішого характеру.
Мінімальний обсяг матеріалу, що вивчається зі стереометрії в основній школі, визначають обов'язкові результати навчання. Наступному накопиченню та переробці у свідомості учнів геометричних фактів, формуванню та розвитку просторових уявлень, конструктивних здібностей має сприяти подана нижче система задач. Для деяких випадків, де це потрібно, описано методику роботи з ними. Задачі підвищеної складності позначено зірочкою (*).
Учні вже мають уявлення про паралельні та перпендикулярні прямі. На другому етапі ми пропонуємо їх перенести і на простір. У зв'язку з цим доцільним є виконання серії вправ на засвоєння учнями взаємного розміщення прямих і площин у просторі. Спочатку це потрібно робити на різних моделях геометричних тіл, поступово переходячи до їх наочних зображень.
Для формування уявлень про взаємне розміщення прямих у просторі, а також прямої та площини, для більшої наочності доцільно використовувати каркасні та скляні моделі. Розглядаючи поняття про взаємне розміщення площин краще користуватися скляними моделями та моделями, виготовленими з картону.
1.На моделі прямої трикутної призми покажіть ребра, які лежать на мимобіжних прямих.
2.На моделі прямокутного паралелепіпеда покажіть ребра, перпендикулярні до нижньої основи.
3.На моделі піраміди покажіть кілька граней, що перетинаються.
4.На моделі циліндра покажіть паралельні грані.
5.Дано модель прямої призми, основою якої є паралелограм. Покажіть:
а) пари паралельних граней;
б) пари перпендикулярних граней.
6. На рис. 18 зображено чотирикутну піраміду SABCD. Назвіть усі ребра, які лежать на прямих, що не перетинають: а) ребро SC; б) ребро AB.
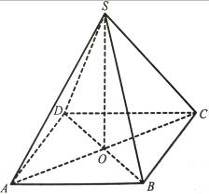
Рис. 18
7. На рис. 19 зображено пряму трикутну призму ABCA1B1C1. Назвіть:
а) ребра, паралельні ребру AA1;
б) ребра, перпендикулярні до ребра BC.
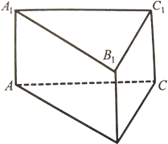
Рис. 19
8. На зображенні прямокутного паралелепіпеда (рис. 20) назвіть:
а) взаємно перпендикулярні грані;
б) грань, паралельну грані BB1C1C.
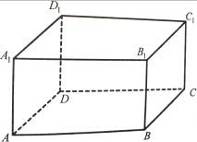
Рис. 20
9. Зобразіть будь-які два відрізки куба (які не є його ребрами) з кінцями у вершинах куба (рис. 21) такі, щоб вони були:
а) паралельними;
б) перпендикулярними;
в) мимобіжними.
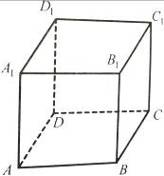
Рис. 21
У 9 класі продовжується формування в учнів уявлень про геометричні тіла за їх розгортками та зображеннями, зокрема під час обчислення площ поверхонь цих тіл за розмірами, поданими на розгортках та зображеннях.
Наведемо приклади таких задач.
10.Розгорткою бічної поверхні циліндра є прямокутник зі сторонами 63 см і 3,2 см. Обчисліть радіус основи циліндра (розгляньте два випадки).
11.Обчисліть площу повної поверхні конуса, якщо твірна конуса дорівнює 12см, центральний кут розгортки 120°.
12.За поданими на розгортках призм розмірами (рис. 22) обчисліть площі їх поверхонь. Основи призм – правильні многокутники. (Одиниці вимірювання подано в дециметрах.)
13.Обчисліть площі поверхонь (бічну та повну) прямих призм за розмірами, поданими на рис. 23. Основи призм – правильні многокутники. (Одиниці вимірювання подано в сантиметрах.)
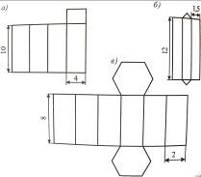
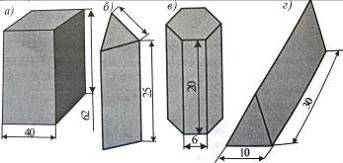
Рис. 22 Рис. 23
Центральне місце на другому етапі відводиться вправам на зображення простіших геометричних тіл. Їх розв'язуванню сприяє попередня підготовча робота, а саме: розпізнавання многогранників і тіл обертання на моделях та їх зображеннях, знаходження плоских фігур на зображеннях геометричних тіл.
Після того як учні ознайомилися з побудовою зображень призми, піраміди, циліндра, конуса, кулі, слід запропонувати їм виконати вправи на закріплення. Зокрема, це можуть бути вправи такого типу.
14. Накресліть прямокутний паралелепіпед і позначте його вершини буквами. Назвіть:
а) ребра, що лежать на паралельних, перпендикулярних, мимобіжних прямих;
б) паралельні, перпендикулярні грані.
15.На зображенні куба проведіть площину так, щоб одержати квадратний переріз куба.
16.На рис. 24 дано зображення куба, на ребрах якого взято три точки. Побудуйте фігуру (переріз), по якій площина, що проходить через дані точки, перетне куб.
17.
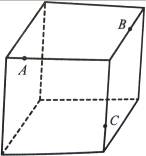
Рис. 24
18.На рис. 25 дано зображення прямокутного паралелепіпеда, на ребрах якого взято три точки. Побудуйте переріз паралелепіпеда площиною, що проходить через дані точки. Яка фігура утворилась у перерізі?
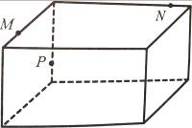
Рис. 25
18.Зобразіть прямий паралелепіпед і проведіть його діагоналі.
19.Зобразіть пряму трикутну призму. Проведіть діагональ бічної грані.
20. Побудуйте зображення прямої трикутної призми. Сполучіть кінці сторони нижньої основи та протилежну вершину верхньої основи. Яка фігура утворилася в перерізі?
21.Зобразіть круговий циліндр. Позначте на зображенні радіус нижньої основи.
22.Зобразіть циліндр та побудуйте зображення його осьового перерізу.
23.Побудуйте зображення циліндра. Позначте точку на колі верхньої основи і точку на колі нижньої основи. Сполучіть їх відрізком.
Похожие работы
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... без опанування системи понять цієї науки. Це великою мірою стосується математики. Найважливішим завданням викладання математики є формування в учнів правильних математичних понять. 1.3. Суттєві і несуттєві властивості понять. Прийоми їх виявлення. Засвоєння математичних понять відбувається у процесі аналітико – синтетичної діяльності учнів, спрямованої на виявлення істотних загальних ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... , тим більше опукло представлені в навчальному процесі, грають у ньому велику роль матеріально-технічні фактори й умови навчання, тим потрібніше моделювання в навчальних цілях як компонент загальнотехнічної підготовки. 2. Реалізація міжпредметних зв'язків між загальноосвітніми і загальнотехнічними предметами (на прикладі математики і креслення). В основі міжпредметних зв'язків математики і ...
0 комментариев