Навигация
Створення моделей просторових об’єктів
3. Створення моделей просторових об’єктів.
Створення об’єкта типу Многогранник.
Для створення об'єкта типу Многогранник потрібно звернутися до послуги меню Об'єкт \ Створити \ Многогранник, що призведе до появи вікна Конструювання об'єкта з вкладкою Многогранник (рис. 29).
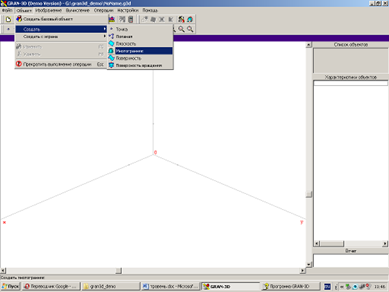
Рис. 29
Засобами ППЗ GRAN-3D можна створити довільний многогранник. Для цього необхідно у відповідних полях вказати кількість вершин многогранника і кількість трикутних граней (не трикутні грані потрібно поділити на трикутники), ввести координати вершин многогранник в таблицю Вершини, а також вказати по три вершини на кожній грані.
Для опуклих многогранників можна не вказувати кількість трикутних граней і номери вершин для кожної грані. Досить спочатку ввести вершини многогранник, а потім скористатися послугою Сформувати межі опуклого об'єкта – кількість граней і відповідні номери вершин для кожної грані будуть встановлені автоматично. Для підтвердження введення даних слід «натиснути» кнопку Виконати.
4. Графічне зображення об’єктів типу Точка, Ламана, Площина.
Об'єкти типу Точка, Ламана і Площина можна задавати «з екрану», вказавши точки, які визначають ці об'єкти, безпосередньо в полі Зображення з допомогою миші. Для створення об'єктів зазначених типів описаним способом слід звернутися до послуги меню Oбьект \ Створити з екрану \ Точка, Oбьект \ Створити з екрану \ Ламана або Oбьект \ Створити з екрану \ Площина, в залежності від того, об'єкт якого типу необхідно створити. На відповідний запит програми, який з'явиться у полі підказки, необхідно в поле Зображення вказати (за допомогою покажчика миші) точки, які будуть визначати об'єкт, після чого з'явиться (після вказівки останньої крапки) вікні Конструювання об'єкта відкоригувати деякі параметри об'єкта (якщо це необхідно) і «натиснути» кнопку Виконати.
Для створення об'єкта типу Точка потрібно вказати лише одну точку.
Для створення об'єкта типу Ламана потрібно вказати стільки точок, скільки вершин має ламана. Вказавши останню вершину ламаної, потрібно натиснути праву клавішу миші.
Для створення об'єкта типу Площина слід вказати три точки, через які має проходити площина.
«Вказати крапку» означає підвести покажчик миші в поле Зображення до зображення будь-якої вершини або лінії (ребра) будь-якого створеного об'єкта так, щоб у полі інформування з'явилися координати точки і назва об'єкта, якому вона належить, і натиснути ліву кнопку миші. Якщо одна з координатних площин розміщена (за допомогою смуг повороту зображення) паралельно площині зображення, тоді можна підвести курсор миші до будь-якої точки площини так, щоб у полі інформування з'явилися координати цієї точки, і натиснути ліву кнопку миші. Координата точки вздовж осі виродження буде вважатися рівна 0.
5. Характеристика об’єктів.
Характеристика поточного об’єкта.
Деякі характеристики об'єктів обчислюються автоматично відразу після створення об'єктів або після їх перетворення (рис. 30). Для об'єктів усіх типів обчислюються (і виводяться в поле Характеристики) мінімальні і максимальні координати точок уздовж кожної з координатних осей. Крім цього, для об'єктів кожного окремого типу виводиться деяка додаткова інформація:
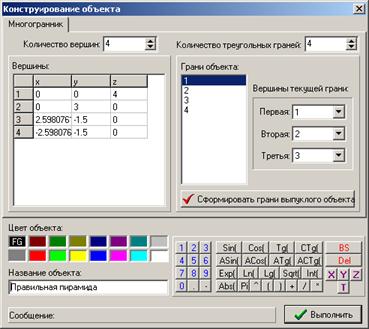
Рис. 30
– для об'єктів типу Ламана обчислюється довжина ламаної, а якщо ламана замкнена і всі її вершини лежать в одній площині, то також обчислюється площа області, обмеженої ламаної;
– для об'єктів типу Площина, незалежно від способу завдання, обчислюються коефіцієнти A, B, C і D рівняння площини виду Ax + By + Cz + D = 0;
– для об'єктів типу Многогранник обчислюється об'єм та площу поверхні, а також площа і периметр окремо кожної грані (ці характеристики наводяться у вікні Перелік граней об'єкта, яке з'явиться при звернення до послуги Обчислення \ Багатогранник \ Площі і периметри граней);
– для об'єктів типу Поверхня можливо обчислення обсягів і площ поверхонь тіл, які ними обмежуються (ці відомості доступні через послугу головного меню Обчислення \ Подвійний інтеграл і площу поверхні);
– для об'єктів типу Поверхня обертання обчислюються площа поверхні, утвореної обертанням графіка деякої функції або ламаного, і об'єм тіла, обмеженого такою поверхнею.
6. Обчислення об’ємів і площ поверхні многогранників.
Обсяги та площі поверхонь об'єктів типу Многогранник (піраміда, призма, паралелепіпед, куб і т.п.) обчислюються автоматично при створенні або перетворення цих об'єктів. Обчислені значення виводяться в поле характеристик поточного об'єкта.
Додаткова інформація про площі та периметри окремих граней поточного многогранника доступна через послугу програми Обчислення \ Многогранник \ Площі і периметри граней. У що з'являється вікні Перелік граней об'єкта наведено перелік граней поточного об'єкта-многогранника та переліки вершин, які лежать на кожній окремій грані, а також площі і периметри цих граней. Під переліком в полі Площа зазначених виводиться сумарна площа граней, зазначених «галочкою» у переліку граней. За допомогою кнопок Позначити всі, Зняти позначки і Інвертувати позначки можна швидко відзначити всі грані, зняти позначки з усіх граней в переліку або змінити стан відміток граней на протилежне. Послугою Обчислення \ Многогранник \ Площі і периметри граней можна скористатися лише тоді, коли поточних об'єктом є об'єкт типу Многогранник.
7. Обчислення об’ємів і площ поверхні тіл обертання.
У програмі передбачено обчислення обсягів і площ поверхонь тіл обертання, що утворюють яких обертаються навколо осі Оx або Oy в прямокутній декартовій системі координат і задаються одним з трьох способів:
1. у вигляді явної залежності між змінними x і y: y = f (x);
2. у вигляді заданої параметрично залежності між змінними x і y: x = f (t), y = g (t), де t – мінлива-параметр;
3. у вигляді ламаної, заданої впорядкованим набором вершин у площині xOy.
Відразу після створення об'єкта типу Поверхня обертання розпочнеться обчислення об'єму та площі поверхні тіла, обмеженого поверхнею, утвореної обертанням графіка заданої функції або ламаного. Цей процес вимагає певного часу, тому під час обчислення з'являється вікно з показником стану виконання обчислень.
Після обчислення результат буде виведено у полі характеристик поточного об'єкта. У програмі передбачено обчислення обсягів і площ поверхонь тіл обертання, що утворюють яких обертаються навколо осі Оx або Oy в прямокутній декартовій системі координат і задаються одним з трьох способів:
1. у вигляді явної залежності між змінними x і y: y = f (x);
2. у вигляді заданої параметрично залежності між змінними x і y: x = f (t), y = g (t), де t – мінлива-параметр;
3. у вигляді ламаної, заданої впорядкованим набором вершин у площині xOy.
Відразу після створення об'єкта типу Поверхня обертання розпочнеться обчислення об'єму та площі поверхні тіла, обмеженого поверхнею, утвореної обертанням графіка заданої функції або ламаного. Цей процес вимагає певного часу, тому під час обчислення з'являється вікно з показником стану виконання обчислень.
Після обчислення результат буде виведено у полі характеристик поточного об'єкта.
Похожие работы
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... без опанування системи понять цієї науки. Це великою мірою стосується математики. Найважливішим завданням викладання математики є формування в учнів правильних математичних понять. 1.3. Суттєві і несуттєві властивості понять. Прийоми їх виявлення. Засвоєння математичних понять відбувається у процесі аналітико – синтетичної діяльності учнів, спрямованої на виявлення істотних загальних ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... , тим більше опукло представлені в навчальному процесі, грають у ньому велику роль матеріально-технічні фактори й умови навчання, тим потрібніше моделювання в навчальних цілях як компонент загальнотехнічної підготовки. 2. Реалізація міжпредметних зв'язків між загальноосвітніми і загальнотехнічними предметами (на прикладі математики і креслення). В основі міжпредметних зв'язків математики і ...

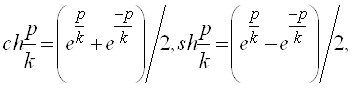
0 комментариев