ОПРЕДЕЛЕНИЕ СОСТОЯНИЯ УСТОЙЧИВОСТИ СИСТЕМЫ

2. ОПРЕДЕЛЕНИЕ СОСТОЯНИЯ УСТОЙЧИВОСТИ СИСТЕМЫ

Состояние устойчивости системы можно определить по корням ее характеристического уравнения. Система, как известно, устойчивая, если все действительные корни отрицательные, а комплексные корни имеют отрицательную действительную часть. При этом апериодический запас устойчивости определяется наименьшим расстоянием к нулю действительных корней, а колебательный запас – наименьшим расстоянием действительной частей комплексных корней. В теории автоматического управления широкого применения приобрели также методы определения состояния устойчивости, которые не требуют решения характеристического уравнения. Их называют критериями устойчивости. Одним из них есть критерий Гурвица, который дает возможность определить состояние устойчивости системы непосредственно по коэффициентам характеристического уравнения.

Характеристический многочлен системы – это знаменатель ее передаточной функции. Поэтому характеристическое уравнение заданной системы имеет такой вид:

 .

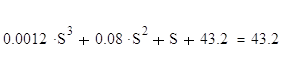Для решения этого уравнения воспользуемся программой MathCad:
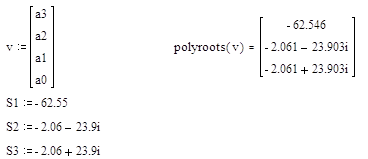Как видно из решения, действительный корень этого уравнения отрицательный, и действительные части комплексных корней также отрицательные.

Следовательно, система устойчивая.

Определим апериодический и колебательный запасы устойчивости.

 

a

 

Рис.1

Т.к. апериодический запас устойчивости равен расстоянию до нуля действительного корня, то он равен а1= -62,55. Колебательный запас равен расстоянию до нуля действительной части комплексных корней, следовательно а2,3= -2,06

3. ИССЛЕДОВАНИЕ ПЕРЕХОДНОГО ПРЦЕССА НЕПРЕРЫВНОЙ СИСТЕМЫ

Как известно, изображение по Лапласу переходной характеристики (ПХ) h(t) определяется таким общим выражением

 ,

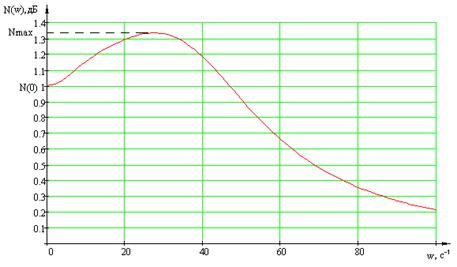
где B(s) и A(s) – в общем случае многочлены соответственно числителя и знаменателя изображения. Функция h(t) имеет вид:

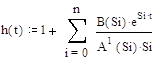
B(Si)=K=43,2

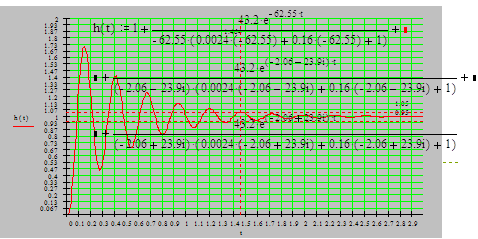
Рис.2 График переходной характеристики

t	0,147	0,279	0,411	0,543	0,675	0,81	0,873	0,936
h(t)	1,71	0,458	1,4132	0,68494	1,24	0,82	1	1,1399

t	1,005	1,071	1,137	1,2	1,266	1,332	1,398	1,464
h(t)	1	0,894	1	1,08	1	0,94	1	1,047

На графике видно, что время переходного процесса tp = 1,464 мс,h(t)max= 1.71,

σ=(1.71-1)*100%= 71%

Эти значения не удовлетворяют заданным условиям и подлежат корректированию.

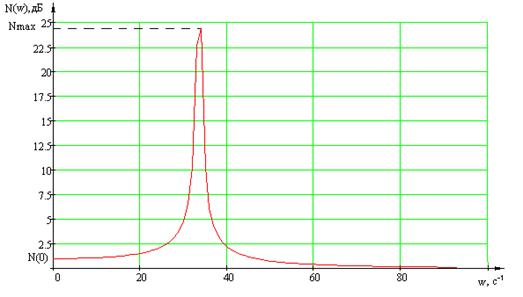
Построим график функции g(t) – импульсной характеристики системы:

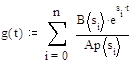
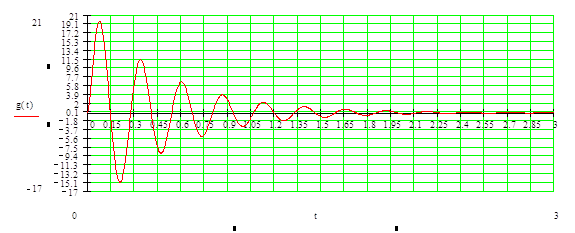
Рис.3 График импульсной характеристики системы.