Навигация
С = С. 10. с = -С 11. с = С 12. с = -С
82482
знака
0
таблиц
0
изображений
9. с = С. 10. с = -С 11. с = С 12. с = -С
b = B b = -B b = B b = -B
n =- N n = N n = N n =- N
13. с = С 14. с = -С
b = B b =- B
n =- N n = N
*******
Итак, рассмотрим случай 5.
Случай 5
(16)
(17´)
(18´)
(19).
Тогда сумма 
имеет вид:
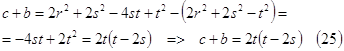
Учитывая (14) и (19), можно получить разность :
=> 
.
Выразим из (25) и (26) :
=> 
=> 
.
По условию должны быть взаимно простыми целыми числами, поэтому их общий множитель 
.
Т.о., имеют вид:
, 
, а их сумма 
.
Т.к. из (8) 
, то 
=> 
.
Из (19) с учетом (29) выразим 
:
, т.е. 
.
Т.о., 
, 
, т.е.
,
выражения которых, с учетом (33), полностью совпадают с (9) и (10).
Теперь, с учетом (17′) и (18´), найдем разность 
:
т.к. , т.е. 
(36´).
(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (29). В последующих действиях мы это учтем).
Теперь, учитывая (32), найдем разность (b-n)-n:
где 
.
Т.к. b + c =2n, то b-2n = b - (b + c) = - c = -1 => c = 1 (40).
Учитывая (34), получим 
=> 
(38´).
Теперь, с учетом (38´), можно получить окончательное выражение для b (из (35)):
, т.е. 
(41).
Таким образом, уравнение 
(15), решениями которого являются (16), (17′), (18´) и (19), в конечном счете, имеет следующие решения:
(41), , где 
- взаимно простые нечетные целые 
(40), (38´), числа
*******
Случай 6
Нетрудно догадаться, что если бы у уравнения (15) были бы решения, противоположные по знаку с решениями (16), (17′), (18´) и (19), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (40), (41), (38´´) и (33), т.е.
(40´), 
(38),
(41´), 
(33´), где - взаимно простые целые нечетные числа.
*******
Случай7
(16)
(17´)
(18´)
(19´)
Тогда сумма имеет вид:
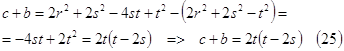
Учитывая (14) и (19´), можно получить разность :
=> 
(26´).
Выразим из (25) и (26´) :
=> 
=> 
.
По условию должны быть взаимно простыми целыми числами, поэтому их общий множитель .
Т.о., имеют вид:
(30´), 
(31´), а их сумма .
Т.к. из (8) , то => .
Из (19´), с учетом (29), выразим :
, т.е. 
(33´).
Т.о., 
, 
, т.е.
(34´),
(35´),
выражения которых, с учетом (33), полностью совпадают с (9) и (10).
Теперь, с учетом (17′) и (18´), найдем разность :
т.к. , т.е. (36´).
(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (29). В последующих действиях мы это учтем).
Теперь, учитывая (32), найдем разность (b-n)-n:
где .
Т.к. b+c=2n, то b-2n = b-(b+c) = -c = -1 => c = 1 (40).
Учитывая (34´), получим 
=> 
(38´´´).
Теперь, с учетом (38´´´), можно получить окончательное выражение для b (из (35´)):
, т.е. 
(41´´).
Таким образом, уравнение (15), решениями которого являются (16), (17′), (18´) и (19´), в конечном счете, имеет следующие решения:
(40), (38´´´),
(41´´), (33´), где - взаимно простые нечетные целые числа.
*******
Случай 8
Нетрудно догадаться, что если бы у уравнения (15) были бы решения, противоположные по знаку с решениями (16), (17′), (18´) и (19´), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (40), (41´), (38´´´) и (33´), т.е.
(40´), 
(38´´),
, 
(33), где - взаимно простые целые нечетные числа.
*******
Вывод
Итак, после анализа полученных решений в Случаях 1,…, 8, уравнение (15) , где c и b – взаимно простые целые нечетные числа, имеет решение в следующих целых числах:
а) 
; 
; 
; ;
б) 
; 
; 
; .
А это в свою очередь означает, что и уравнение 
при вышеназванных условиях (смотри Утверждение1) может иметь целые решения либо при , либо при 
.
Случай 9
(16)
(17)
(18´)
(19)
Из (16) и (17) имеем:
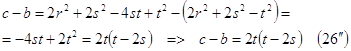
Учитывая (14) и (19), можно получить разность 
другим способом:
=> .
Следовательно,
=
=> 2t = 4r (
≠ 0, т.к. в (26´´) с ≠ b) => t = 2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых 
решений.
*********
Случай 10
(16´)
(17´)
(18)
(19´),
т.е. по сравнению с предыдущим случаем 9 здесь знаки перед скобками противоположные, а потому (по понятным причинам) результат будет таким же, что и в случае 9.
Действительно, из (16´) и (17´) имеем:
Учитывая (14) и (19´), можно получить разность другим способом:
- => 
.
Следовательно, -=-=> 2t = 4r ( ≠ 0, т.к. в (26´´) с ≠ b) => t = 2r (32´) => в (16´) и (17´) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.
********
Случай 11
(16)
(17)
(18)
(19´)
Из (16) и (17) имеем:
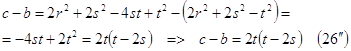
Учитывая (14) и (19´), можно получить разность другим способом:
- => .
Следовательно, =-=> 2t = - 4r ( ≠ 0, т.к. в (26´´) с ≠ b) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.
Случай 12
(16´)
(17´)
(18´)
(19),
т.е. по сравнению с предыдущим случаем 11 здесь знаки перед скобками противоположные, а потому (по понятным причинам) результат будет таким же, что и в случае 11.
Действительно, из (16´) и (17´) имеем:
Учитывая (14) и (19), можно получить разность другим способом:
=> .
Следовательно, -==> 2t = - 4r ( ≠ 0, т.к. в (26´´) с ≠ b) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.
*******
Случай 13
(16)
(17)
(18´)
(19´)
Из (16) и (17) имеем:
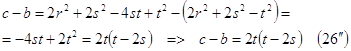
Учитывая (14) и (19´), можно получить разность другим способом:
- => .
Следовательно, =-=> 2t = - 4r ( ≠ 0, т.к. в (26´´) с ≠ b) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.
********
Случай 14
(16´)
(17´)
(18)
(19),
т.е. по сравнению с предыдущим случаем 13 здесь знаки перед скобками противоположные, а потому (по понятным причинам) результат будет таким же, что и в случае 13.
Действительно, из (16´) и (17´) имеем:
Учитывая (14) и (19), можно получить разность другим способом:
=> .
Следовательно, -==> 2t = - 4r ( ≠ 0, т.к. в (26´´) с ≠ b) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых решений.
***********
Вывод.
Похожие работы
... , что возможно, наша цивилизация подойдет к концу прежде, чем удастся доказать Великую теорему Ферма. Доказательство Великой теоремы Ферма стало самым ценным призом в теории чисел, и поэтому не удивительно, что поиски его привели к некоторым наиболее захватывающим эпизодам в истории математики. В эти поиски оказались вовлеченными величайшие умы на нашей планеты, за доказательство назначались ...
... Декарт в первую очередь идеолог: он основатель философской школы, он формирует понятия, совершенствует систему буквенных обозначений, но в его творческом наследии мало новых конкретных приемов. В противоположность ему Пьер Ферма мало пишет, но по любому поводу может придумать массу остроумных математических трюков (см. там же “Теорема Ферма”, ”Принцип Ферма”, ”Метод бесконечного спуска Ферма”). ...
... Z 12 30 (15) При рассмотрении вопроса о Пифагоровых тройках не было целью составление таблиц этих троек. Ибо целью этой статьи является показ возможностей алгоритма решения Диофантовых уравнений. Решение уравнения Каталана Уравнение данного вида получается при попытке решения гипотезы Биля. Поэтому решение данного уравнения является как бы леммой гипотезы Биля. Ответ будет ...
... ) и теория диофантового приближения (раздел теории чисел, в котором изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов). 2.6. Теон и Гипатия Учеными, завершившими цикл математиков Александрийской школы, были Теон (IV в.) и его дочь Гипатия (370—415). Теон проделал большую работу, комментируя труды Евклида и Птолемея. Что же касается Гипатии, то, по отзывам ...
0 комментариев